梁構造物の幾何学的非線形問題の有限要素法解析は特に興味の持たれる分野であり、多くの研究者により様々な解析法が開発されてきた。しかし、解析を2次元から3次元に拡張した場合、有限回転をベクトル量として取り扱うことができないという問題点が生じ、そのために、3次元大変形解析には有限回転の非ベクトル性を考慮した歪-変位関係式や構成方程式が必要となる。ところが、これらの方程式は変位の複雑な関数となるため、それ自身がわかりにくいものであるばかりでなく、有限要素法の定式化の際におこなわれる、支配方程式の線形化に用いられる近似も複雑でわかりにくいものとなることが多い。そのために、その仮定がどのような問題にまで適用可能であるかの判断をすることが難しく、あまり普及していないのが現状である。 一方、梁構造物の大変形問題には、変形が進むにつれて、変位は大きくなっていくが、歪は小さいままであるという特徴がある。したがって、要素の剛体回転とともに回転していく共回転座標系(co-rotational coordinates)を考えると、共回転座標系への座標変換により、全体座標系での変位から剛体回転・剛体変位成分が取り除かれるため、共回転座標系での変位は微小な値となる。ゆえに、共回転座標系を要素座標系に用いれば、要素座標系内で微小変形の仮定を用いた場合にも十分な精度の解を期待できる。そこで、近年、梁構造物の3次元有限要素解析法として、共回転要素座標系を用い、要素座標系内では微小変位,微小回転の仮定が成り立つものとして、線形の歪-変位関係式で要素の定式化をおこない、問題の非線形性を要素座標系から全体座標系への座標変換に持たせるという手法が提案された。この方法には、要素座標系内で線形の歪-変位関係式や構成方程式を用い、有限回転の非ベクトル性の影響を無視することができるという利点があり、要素の歪と応力を、要素座標系内で線形近似をおこなうこと以外は厳密に、しかも他の方法と比べ極めて簡単な式で計算することができるという特徴がある。しかし、問題の非線形性をすべて座標変換に持たせているため、その座標変換マトリクスを、有限回転の非ベクトル性の影響を含めて厳密に求める必要がある。ところが、梁構造物の有限要素法解析には、1次元的な梁要素が用いられることが多く、この要素を用いた場合には、要素座標系の定義に多くの節点自由度を用いた計算が必要とされる。そのために、従来の研究では、要素座標系自体を近似的に求めたり、座標変換マトリクスの一部分を計算の都合上無視するなど、この座標変換を厳密に取り扱ったものは存在しなかった。 そこで本研究では、上記のような共回転要素座標系を用いる方法に基づきながらも、従来の研究の問題点である要素座標系への座標変換マトリクスの導出を厳密におこない、要素座標系内での線形近似以外の特別な近似を用いることのない、しかも簡便かつ有効な、梁構造物の3次元大変形の有限要素解析法の開発を目的として、以下のことをおこなった。 まず、要素座標系への座標変換マトリクスに含まれる、有限回転の非ベクトル性の影響を調べるために、有限回転を表わす擬回転ベクトルの変分量と、擬回転ベクトルがその変分量だけ変化する微小回転移動を表わす微小回転ベクトルとの変換マトリクスを求めた。その結果、回転が3次元であるならば、この2つのベクトルは、擬回転ベクトルの回転角が微小な場合にも一致しないことが確認された。 次に、厳密に座標変換マトリクスを求めることが容易にできるように、用いる要素を選択し、要素座標系を定義した。用いたのは、通常の2節点の梁要素ではなく、要素の中央部に1つ節点を追加した3節点の梁要素である。その理由は、要素の中央部の節点(節点2とする)の回転角が、常に要素全体の回転角のほぼ平均的な値となるため、それを要素の剛体回転とみなし、その回転マトリクスをそのまま要素座標系の全体座標系からの回転角を表わす回転マトリクスとして用いることができるからである。このように要素座標系を定義した場合の座標軸は、図1のようになる。この要素座標系内で微小変形・微小回転の仮定を用いて、要素の線形の剛性マトリクスを定式化した。  図1 要素座標系の定義 そして、この要素座標系と上記の擬回転ベクトルの変分量についての変換マトリクスを利用することにより、全体座標系から要素座標系への座標変換マトリクスを厳密に、しかも従来の研究よりも簡略に導出することができた。そして、この座標変換マトリクス自体も、要素の節点自由度にあまり依存しない形で求められたため、その変分をとる計算においても一切の特別な近似を必要としなかった。その結果、要素座標系で求めた要素の線形剛性マトリクスを全体座標系での接線剛性マトリクスへ変形する計算を、厳密におこなうことができた。 このようにして求められた要素の接線剛性マトリクスは、他の3次元大変形解析の研究と同様に、非対称となった。しかし、座屈解析等にはその計算のアルゴリズム上、剛性マトリクスは対称のものが求められるので、まず、座屈を起こさない3個の大変形問題を解析し、求められた接線剛性マトリクスを対称化した場合にも、得られる計算値の精度が悪化しないことを示した。 そして、この対称化した接線剛性マトリクスを用いて、他の研究で解析されたことのある、座屈後に3次元変形をする5個の例題について解析をおこなった。その結果の一部を図2,図3に示す。図2はCable Hocklingと呼ばれる、一端固定、もう一つの端は梁の軸方向の並進移動とその回りの回転のみ可能な直線梁の、ねじりモーメントによる座屈問題について、その初期形状と変形形状を示したものであり、図3は直線梁をねじった状態で両端の回転角を固定し、その後圧縮するというねじり圧縮問題について、初期形状と初期ねじり角が のときの変形形状を示したものである。これらを含め、本研究の方法による解析の結果と、他の研究の結果を比較・検討したところ、両者はよく一致していた。 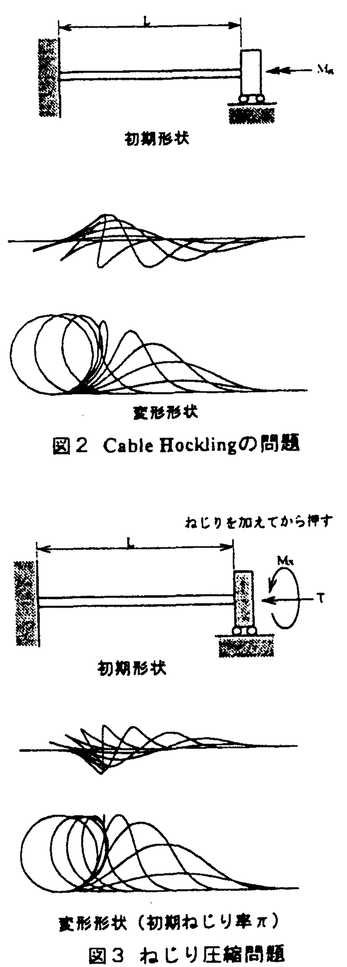 図表図2 Cable Hocklingの問題 / 図3 ねじり圧縮問題 その後、図4に示すような、中央部に鉛直下向きの集中荷重を受ける両端固定のアーチの座屈解析をおこなった。その結果、最も座屈荷重の小さい座屈モードは、アーチの形状の深い浅いにかかわらず、2次元変形のときに知られている非対称座屈ではなく、中央部(荷重点)が面外に倒れこむような3次元対称変形をするものであることがわかった。そこで、この問題についての実験をおこない、このモードの座屈が起こることを確認することにした。ただし、使用する試験片の材質(ピアノ線を使用)から、実験は初期変形のあるアーチでおこなった。そして、実験したすべての中心角のアーチについて、その座屈後の変形が、荷重点が面外に倒れこむ3次元対称変形であることを確認した。ところで、この実験値と計算値を比較するためには、計算に上記の初期変形の影響と、アーチ全体の自重が計算で予測された座屈荷重の1/10程度であったことから、自重の影響を加える必要があった。しかし、本研究の方法は有限要素法であるため、自重や初期変形の影響を簡単に計算に加えることができた。そして、その計算値と実験値を比較したところ、両者はよく一致していた(図5,図6)。  図表図4 アーチの初期形状 / 図5 荷重と荷重点の荷重方向変位の関係(中心角180°のアーチ) / 図6 荷重と荷重点の荷重方向変位の関係(中心角60°のアーチ) 以上のことから、本研究で示した方法は、他の研究と比べてかなり簡単なものであるにもかかわらず、その精度は他の研究と同等であることが確認された。(さらに、自重等の影響を無視することのできない実際の構造物の大変形解析にも、有限要素法であるがゆえに、特別な苦労なく応用することが可能なことも確認された。)これは、要素座標系での線形近似以外には、解法を簡略化するための近似を一切おこなわず、厳密に座標変換マトリクス等の定式化をおこなったことによるものである。したがって、本研究の提案する有限要素の定式化法は、梁構造物の3次元大変形解析には最適なのもの一つであると考えられ、ゆえに本研究は構造力学上意義のあるものであるといえる。 |