| 内容要旨 | | 何故N( 3)体問題が解けないかを今日の知見に照らし合わせて答えるならば,それはその系が積分不可能系であるからということになる.しかし,具体的な少数自由度系(自由度2または3の系)を与えて,その積分不可能性を証明できるようになったのは1983年のヂグリン,1987年の吉田等による最近の研究からである.ところで,多自由度ハミルトン力学系は,統計力学の基礎,実際の物性とも深く関わり,又数値計算には大自由度カオス特有のアーノルド拡散と呼ばれる現象があり,本質的に計算困難であるので,その積分可能性を有限の手順で判定することは,単に非線形力学系の問題にとどまらず重要な問題とされていた.ところが,その多自由度積分不可能性判定は,非共鳴条件というボトルネックがあるため今まで未解決であった.実際,自由度3のハミルトン力学系 3)体問題が解けないかを今日の知見に照らし合わせて答えるならば,それはその系が積分不可能系であるからということになる.しかし,具体的な少数自由度系(自由度2または3の系)を与えて,その積分不可能性を証明できるようになったのは1983年のヂグリン,1987年の吉田等による最近の研究からである.ところで,多自由度ハミルトン力学系は,統計力学の基礎,実際の物性とも深く関わり,又数値計算には大自由度カオス特有のアーノルド拡散と呼ばれる現象があり,本質的に計算困難であるので,その積分可能性を有限の手順で判定することは,単に非線形力学系の問題にとどまらず重要な問題とされていた.ところが,その多自由度積分不可能性判定は,非共鳴条件というボトルネックがあるため今まで未解決であった.実際,自由度3のハミルトン力学系  の積分不可能性が吉田によって初めて証明されたのは1989年のことである.この様な状況のもと,この論文では,多自由度系の積分不可能性証明の困難の源であった非共鳴条件に如何に対処するかという問題に焦点を絞り,以下の 1.大城的かつ対称な結合を持つハミルトン系(自由度3以上の任意の有限自由度) 2.鏡映対称性を持つ一次元非線形格子(自由度3以上の任意の有限奇数自由度)の二種類の系の積分不可能性を初めて厳密に示す. 二種類のモデルうち前者のモデルは「多自由度ハミルトン系の積分不可能性にとって本質的な判定条件は何か?」を探る為,著者が考案したモデルであり,具体的には次のハミルトニアン  で記述される.但し,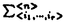 は1,2,…,nから選ばれるr種の全ての組み合わせについて和をとることを表し,r( は1,2,…,nから選ばれるr種の全ての組み合わせについて和をとることを表し,r( n)は3以上の整数,sは1以上の整数とする.この論文では便宜上,type(n,r,s)と呼ぶ.後者のモデルは実際の物質をより意識した一次元非線形格子模型であり,今まで熱伝導などの非平衡現象を調べるのに数多くの数値計算が行われてきたモデルである.この論文ではハミルトニアンを n)は3以上の整数,sは1以上の整数とする.この論文では便宜上,type(n,r,s)と呼ぶ.後者のモデルは実際の物質をより意識した一次元非線形格子模型であり,今まで熱伝導などの非平衡現象を調べるのに数多くの数値計算が行われてきたモデルである.この論文ではハミルトニアンを  として,ポテンシャル関数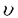 (x)が偶数次の項だけを持つ多項式 (x)が偶数次の項だけを持つ多項式  で与えられるとした.2m=4の時のハミルトニアンが,後にソリトン研究の源となったフェルミ,パスタ,ウラムによってエネルギー等分配則が調べられた調和項に四次の非線形項のついたFPU格子となる. この論文の第二章では,まず.このモグルtype(n,r.s)(2)が従来のヂグリン,吉田型の非共鳴条件を用いた判定条件で扱えないこと,つまりこのtype(n,r,s)(2)が仮に積分不可能であっても従来の方法では判定できず,新しい方法が必要であることを示した.ヂグリンの定理の主張(1983年)は第一章で概観するように自由度2では,「もし系にハミルトニアンH以外に正準変数に関し一価解析的な積分があるならば,ある周期解の周りの変分方程式の直交成分である直交変分方程式の持つ非共鳴なモノドロミー行列m1が存在したとき,m1とは異なる任意のモノドロミー行列m2に対して,可換  もしくは,trm2=0となる」ことであり,一般に非可換なモノドロミー行列に大きな制約を与えるものである.尚ここで自由度nの系の直交変分方程式のモノドロミー行列は(2n-2)×(2n-2)であり,2n-2個の固有値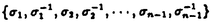 に対して, に対して,  なる関係を満足する整数{lv}が,自明の場合l1=l2=…=ln-1=0を除き存在しない場合に,非共鳴なモノドロミー行列と言う.ヂグリンの定理は自由度3以上でも同様に成立し,ポテンシャルが同次式である場合に吉田(1987年)によって拡張されているが,同様に非共鳴条件を使っている.自由度2の時は, 1が1のベキ根でないことが非共鳴条件になり,例えばSU(2)ヤン=ミルズ場の自由度2のハミルトン系 1が1のベキ根でないことが非共鳴条件になり,例えばSU(2)ヤン=ミルズ場の自由度2のハミルトン系  がハミルトニアン以外に正準変数{qv,pv}v=1,2の1価解析的な関数で表されるクラスの積分がハミルトニアン以外に存在しないことを証明するのに,ある特別解の周りの直交変分方程式のモノドマミー行列がexp(4 ),exp(-4 ),exp(-4 )で与えられる非共鳴なものであることが利用された(ヂグリン,1983年).ところがtype(n,r,s)では,特に自由度4以上では,どの特別解を選んでも,モノドロミー行列の固有値が縮退してしまい,明らかに上の非共鳴条件を満足しない.そこで著者は「非共鳴条件」が強すぎると考え,それに替えて「非共鳴的縮退条件」という新しいモノドロミー行列に対する条件を考えた.ここでモノドロミー行列が「非共鳴縮退的」というのは,モノドロミー行列の固有値が, )で与えられる非共鳴なものであることが利用された(ヂグリン,1983年).ところがtype(n,r,s)では,特に自由度4以上では,どの特別解を選んでも,モノドロミー行列の固有値が縮退してしまい,明らかに上の非共鳴条件を満足しない.そこで著者は「非共鳴条件」が強すぎると考え,それに替えて「非共鳴的縮退条件」という新しいモノドロミー行列に対する条件を考えた.ここでモノドロミー行列が「非共鳴縮退的」というのは,モノドロミー行列の固有値が,  のようにd種類に縮退していても,そのd個の代表固有値が非共鳴条件を満足している場合のこととする.明らかに,この条件は非共鳴条件を含むより広い条件である.さて第二章で展開される異体的な計算で,このtype(n,r,s)は少なくとも2種類の「非共鳴縮退条件」を満足するモノドロミー行列が存在することがわかった.よって著者はこの事実をヒントに非共鳴条件を,非共鳴縮退条件に置き換えることで,「type(n,r,s)の様に,粒子変換に対して対称,かつポテンシャルが同次式のn自由度のハミルトン系を考える.そのときもし,系が角運動量piqi-qipiの関数のみで書かれる積分以外の解析的積分が存在するとする.そのとき,2種類の非共鳴縮退条件を満足するモノドロミー行列が存在するなら,そのn-1個の内の少なくとも1つの小ブロック行列どうしが可換になる」という定理を得た.これはヂグリン=吉田型の定理の拡張となっている.この定理により,表1に示すn,r,sについて,n自由度のハミルトン力学系type(n,r,s)の積分不可能性を示すことが出来た.  表1:第二章で積分不可能性が証明されたハミルトン力学系 表1:第二章で積分不可能性が証明されたハミルトン力学系 第三章では,1989年の同次型一次元非線形格子 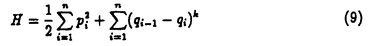 の積分不可能性に関する吉田の結果が,k=4の場合には,FPU格子を含む,非同次型一次非線形格子(3)まで拡張され得ることを示した.吉田は,n個のコワレフスキー指数の非有理部分  が有理数体上一次独立なら(それはモノドロミーの非共鳴条件に対応する),系(9)はハミルトニアン以外に大城的かつ一価解析的た保存量を持ち得ないことを示した.ただしkは4以上の偶数,nは3以上の奇数である.これは,この第三章を通じて課される条件である.第三章で著者は非同次非線形格子(3)の複素時間t上の超楕円関数で表さられるタイプの特別解qi=Ci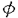 (t)(図1参照)を見つけ,特異点の周りでの分岐は実際にn個の数(10)で特徴づけられることを示した. (t)(図1参照)を見つけ,特異点の周りでの分岐は実際にn個の数(10)で特徴づけられることを示した.  図1:The Initial Lattice Displacements in the Complex Plane(n=7)( 図1:The Initial Lattice Displacements in the Complex Plane(n=7)( <0) <0) 特にFPUタイプのモデルは,解が,式(4)のパラメータ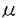 2, 2,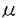 4,nを使って具体的に, 4,nを使って具体的に,  と書けることがわかる.但し, は系のエネルギー,cn(k;t)は母数kのヤコビのcn楕円関数で,更にk,aも具体的にシステムのパラメータで記述され得る量である.この時に限り式(11)のcn(k;at)の極型特異点を一周する周期解のモノドロミー行列の特性指数とn個の数(10)が一致して,ヂグリン=吉田型の積分不可能性判定条件が使える.よって,著者は非同次FPU格子に関し,定理「もしn個の数 は系のエネルギー,cn(k;t)は母数kのヤコビのcn楕円関数で,更にk,aも具体的にシステムのパラメータで記述され得る量である.この時に限り式(11)のcn(k;at)の極型特異点を一周する周期解のモノドロミー行列の特性指数とn個の数(10)が一致して,ヂグリン=吉田型の積分不可能性判定条件が使える.よって,著者は非同次FPU格子に関し,定理「もしn個の数 が有理数体上一次独立なら,この系はエネルギーが零に近いところで解析的な積分がハミルトニアン以外に存在したいこと」を示した. が有理数体上一次独立なら,この系はエネルギーが零に近いところで解析的な積分がハミルトニアン以外に存在したいこと」を示した. 第四章では第三章の結果を踏まえて,n個の数(10)が実際に有理数体上一次独立であることを証明した.これは最終的に一次元非線形格子(9)(四,六,八…次),(3)(四次)の非可積分性を証明したことく他ならない.その有理数体上一次独立性の証明の概略を以下に示す.基本的な方針は(10)の有理数体Qからの拡大次数を円分体上のガロア理論を使って評価することにある.まず(10)が一意的に1の2(n+1)乗根(原始根) を使って書き換えられることに着目する,このとき円分体上のガロア理論によると, を使って書き換えられることに着目する,このとき円分体上のガロア理論によると, の満たす最小既約多項式の次数はちょうどガロア群の位数 の満たす最小既約多項式の次数はちょうどガロア群の位数 (2(n+1))に等しいことがわかっている.但し (2(n+1))に等しいことがわかっている.但し はオイラー関数と呼ばれているものである.そのことを使うと数 はオイラー関数と呼ばれているものである.そのことを使うと数 jがj≠ jがj≠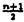 以外の場合には有理数に 以外の場合には有理数に を添加した体Q( を添加した体Q( )に於いても一番外側のルートが外れないことを示すことができる.もし有理数体上で一次の関係式が(10)にある2個以上の互いに異なる数 )に於いても一番外側のルートが外れないことを示すことができる.もし有理数体上で一次の関係式が(10)にある2個以上の互いに異なる数 jどうしであるとする.するとその関係式を変形して二乗した式よりj≠ jどうしであるとする.するとその関係式を変形して二乗した式よりj≠ 以外の数 以外の数 jに於いて体Q( jに於いて体Q( )上でルートが外れなければならないという結論が出てくる.これは先ほどの円分体のガロア理論との帰結に矛盾する. )上でルートが外れなければならないという結論が出てくる.これは先ほどの円分体のガロア理論との帰結に矛盾する. 以上の第二,三,四章をもって当論文の目標である自由度3以上のハミルトン力学系の積分不可能性証明することが,上に挙げた2種類の幅広いクラスの系で達せられた. |