数理物理学において、様々な変形理論の研究は、ここ数年めざましい発展を遂げた。多くの低次元の模型を厳密に解くために、非摂動的方法が発展させられた。成功の主な理由は、これらの模型が無限次元の対称性を持つことである。2次元量子場の理論、2次元古典格子統計模型、量子スピン鎖模型等の研究により、無限次元対称性を取り扱うための、極めて多くの技術が蓄積された。 Kac-Moody代数は、無限次元代数を記述するために導入された。それは、有限型、アフィン型、不定型という3つのクラスに分けられる。我々にとって最も重要なのは、アフィン型のKac-Moody代数である。例えば、2次元の臨界点上での場の理論である共形場の理論においては、アフィンKac-Moody代数は物理的空間を記述するための欠くべからざる道具である。 共形場の理論等で得られた様々な技術の、非臨界点における場の理論への応用は自明ではなかったが、非臨界点での理論の研究の中で、Drinfeldと神保によってKac-Moody代数の、ある種のq-変形理論、「量子代数」(量子群と呼ばれることも多い)が発見された。アフィン型のKac-Moody代数の類似物である"量子アフィン代数"は、みごとに非臨界な可積分理論の無限次元対称性を記述する。共形場の理論のマッシヴ変形であるsine-Gordon理論、XXZスピン鎖模型の非等方変形であるXXZスピン鎖模型等くついての非常に進んだ解析が知られている。 一般に、カレント代数の自由場表示を用いると、オペレーターの真空期待値や、状態空間上でのトレース等の計算を著しく簡単化することがある。したがって、量子アフィン代数の自由場表示が存在すれば、それは非臨界点の理論を研究するための強力な道具になると期待される。本論文では、量子アフィン代数Uq( N)の自由場表示を構成する。また、Uq( N)の自由場表示を構成する。また、Uq( 2)の場合について、任意のn-点相関関数の計算を行い、そのJackson積分公式を導く。 2)の場合について、任意のn-点相関関数の計算を行い、そのJackson積分公式を導く。 紙面の都合上、以下にU’q( 2)の自由場表示の概略だけを述べる。量子アフィン代数U’q( 2)の自由場表示の概略だけを述べる。量子アフィン代数U’q( 2)は、Q(q)上の結合代数で1を持ち、次のような関係式を満たす生成元e0,e1,f0,f1, 2)は、Q(q)上の結合代数で1を持ち、次のような関係式を満たす生成元e0,e1,f0,f1, , , で生成される: で生成される:  ここに、a00=a11=-a01=-a10=2とする。この代数のボゾン化を行うために、つぎの3つのボゾン場a、b、cを導入する。ある複素数kを定め、ボゾンのモード{an,bn,cn,Qa,Qb,Qc|n∈Z}に次の交換関係を与える:  次のようにボゾン場a(z; )を定義する: )を定義する:  また、ボゾン場 ±(z)を ±(z)を  と定義する。ボゾン楊bとcについても同様の定義をする。つぎのような略記をすることがある: 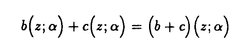  カレント カレント を を 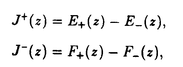 と定義する。ここに、  と定める。さらに、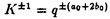 とする。すると、対応 とする。すると、対応  により、代数の準同型を得る。ゆえに、量子アフィン代数Uq( 2)の、レベルkの自由場表示を得た。論文中では、さらにスクリーニングカレントや、頂点作用素等のボゾン表示を議論し、n個の頂点作用素の積の真空期待値を計算する方法を述べる。 2)の、レベルkの自由場表示を得た。論文中では、さらにスクリーニングカレントや、頂点作用素等のボゾン表示を議論し、n個の頂点作用素の積の真空期待値を計算する方法を述べる。 |