素粒子の統一理論の一つの候補として、弦理論が注目されてから久しい。弦は有限の広がりを持った対象であるため、点粒子には無い特有の性質を持つことが期待される。統一理論の観点に立てば、それは時空の幾何を記述していると思われる。従って、弦理論を調べることにより場の理論から来る量子補正が自然な形で現れる可能性があり、幾何学的に新しい側面が見えて来ることが、期待される。弦理論の相関関数を考えた時、リーマン面上のモジュライ空間依存性と共に、ターゲット空間依存性も存在する。特に臨界的弦理論のコンパクト化の問題と関連して、複素3次元カラビ・ヤウ多様体Mが重要な役割をする。その多様体のモジュライ空間の特性により粒子の持つ性質(湯川結合定数等)が決定付けられる。特に複素3次元Mの場合、2つのモジュライ空間(1)ケーラーモジュライ空間、(2)複素構造モジュライ空間が存在し、それぞれを記述する場の理論としてA(M)模型、B(M)模型が存在する。B-模型の相関関数が量子補正を受けないのに対して、A-模型は正則写像 から来る非摂動効果が存在し、その特性を研究することは従来、大変困難であった。 から来る非摂動効果が存在し、その特性を研究することは従来、大変困難であった。 近年カラビ・ヤウ多様体Mに対し、その2つのモジュライ空間の役割を入れ換えたWが存在することが例証され、更にA(M)模型のObservable  [ [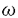 ]の相関関数〈 ]の相関関数〈 [ [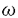 ]… ]… [ [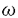 ]〉AとB(W)模型のObservable ]〉AとB(W)模型のObservable  [ [ ]の相関関数〈 ]の相関関数〈 [ [ ]… ]… [ [ ]〉Bの対応(ミラー対称性)が例証されつつある。 ]〉Bの対応(ミラー対称性)が例証されつつある。 私は、特に種数0のリーマン面の場合について、ターゲット空間として複素d-次元カラビ・ヤウ多様体(主に次の(I),(I’),(II))を取り上げ、そのA-模型のOperatorのCorrelatorの特性をミラー対称性の下で調べた。  A(M)模型、B(M)模型は(擬)位相的場の理論であるため基本的構成要素である二点相関関数、三点相関関数によって特徴付けられる。B(W)模型はWのホッジ構造によって既定されるが、それは周期積分  によって指定され、複素構造はその変形によって記述される。そこで、(基本変形後の)周期行列 によって指定され、複素構造はその変形によって記述される。そこで、(基本変形後の)周期行列 の満たす微分方程式∂i の満たす微分方程式∂i =Ci =Ci が持つ複素構造の変形の情報をミラー対称性の下でA(M)模型のオペレーター積の構造 が持つ複素構造の変形の情報をミラー対称性の下でA(M)模型のオペレーター積の構造 に翻訳することによりA(M)模型の三点相関を解析的な形で得た。(模型(I)の三点相関については、計算機による数値的結果が限られた次元dに対して部分的に存在するが、私は(I)について、すべての次元に対する三点相関について解析を行い、今まで議論の無かった解析的な新たな結果、例えば に翻訳することによりA(M)模型の三点相関を解析的な形で得た。(模型(I)の三点相関については、計算機による数値的結果が限られた次元dに対して部分的に存在するが、私は(I)について、すべての次元に対する三点相関について解析を行い、今まで議論の無かった解析的な新たな結果、例えば  等を得た)。三点相関関数について言えば、更により広い範囲の模型、例えば(I’),(II)に対しても適用できる枠組をモノドロミー変換のサイクルの作用の考察と併せて新たに得た。模型(II)については結果は次の通りである。  模型(II)に対しては、ケーラーモジュライが2次元であるため、それに応じてOperator ,(a=1,2)が2個存在する。そのため結合定数 ,(a=1,2)が2個存在する。そのため結合定数 の間のassociativity の間のassociativity  が重要になるが、その解析を行い、関係の成立を得た。 が重要になるが、その解析を行い、関係の成立を得た。 こういった三点相関関数等は正則な関数として表されている。一方、ケーラーモジュライ全体としては、正則部分とのミキシングの効果が存在し、それを表すものとしてエルミート計量が存在する。これを解析するため、N=2超対称非線形シグマ模型から2つの位相的理論A(M)模型、A*(M)模型を新たに考えた。A(M)模型、A*(M)模型それぞれのBRST Observable , , を考え、その間の二点相関 を考え、その間の二点相関 によって定まる(ケーラーモジュライ空間上のmeasureを定める)エルミート計量を考えた。N=2ランダウ・ギンツブルグ模型の枠組でのtt* fusionと類似の手法を、今のA-,A*-模型に対して新たに適用することにより によって定まる(ケーラーモジュライ空間上のmeasureを定める)エルミート計量を考えた。N=2ランダウ・ギンツブルグ模型の枠組でのtt* fusionと類似の手法を、今のA-,A*-模型に対して新たに適用することにより の満たすべき方程式を導いた。その方程式はA-模型のオペレーター積の構造によって決定づけられるものである。結果を模型(I),(I’)に対して適用し の満たすべき方程式を導いた。その方程式はA-模型のオペレーター積の構造によって決定づけられるものである。結果を模型(I),(I’)に対して適用し =exp(qn)に対する方程式が非アフィン戸田方程式であることを新たに導きだした。 =exp(qn)に対する方程式が非アフィン戸田方程式であることを新たに導きだした。  この結果はカラビ・ヤウA(M)模型のインスタントン補正が非線形ソリトン系と関連づけられた最初の具体例である。非アフィンの特性はオペレーター積の構造によって定まり、カラビ・ヤウ多様体の第一チャーン類が0であることに依っていることが判明した。適切な境界条件の下で解の具体的構成を行い の性質を解析した。更に、これらの結果を用い、模型(I)の場合、一般の次元dにたいして、リーマン面が種数1の場合の分配関数の具体的表式を得た。最後にインスタントン補正をソリトン系の方向から理解するという方向を目指し、ここで得られた種々の結果の形式的な自由場表示を与えた。 の性質を解析した。更に、これらの結果を用い、模型(I)の場合、一般の次元dにたいして、リーマン面が種数1の場合の分配関数の具体的表式を得た。最後にインスタントン補正をソリトン系の方向から理解するという方向を目指し、ここで得られた種々の結果の形式的な自由場表示を与えた。 |