高分子物理学において、絡み合い効果が重要であることはよく知られている。実験的には、それは高分子希薄溶液の粘性、高分子の拡散、高分子液体の粘弾性などによって観測される。しかし、その数学的な取扱いは非常に難しいために、従来の理論では絡み合いを無視するかまたは平均場的に取り扱われてきた。レプテーション模型(チューブ模型)は、絡み合いの頻繁に起こる状況下で物理量を計算するという点で優れた理論であるが、絡み合いの詳細な情報は全て平均場で置き換えられてしまう。そのため、その妥当性は明かではない。 通常、高分子の空間配位を表す数学的模型としてランダムウオークを用いることが多い。著者は、閉じたランダムウオーク(ランダム結び目)のトポロジーを、結び目不変量を数値的に計算することで調べた。この研究により、従来の理論では取り扱いの難しかった自分自身の絡み合いを厳密に扱うことができる。以下では、高分子物理学で通常呼ばれる絡み合いと区別するために、これをトポロジー的な絡み合いと呼ぶことにする。 実験的には、輪状DNA、輪状高分子鎖などの物質が見つかっている。輪状DNAを電気泳動にかけると、結び目の種類に応じてバンドができることが観測されており、この原因は結び目の広がりの大きさの違いによると考えられる。さらに、輪状DNAのトポロジーを変える酵素(トポアイソメラーゼ)も現在では見つかっている。輪状高分子に対しては、線状高分子との物性の違いが測定されている。例えば、 温度(見かけ上排除体積効果が無視できる温度)のズレが観測される。これらの現象は、輪状高分子鎖のトポロジー的効果によるものと思われる。 温度(見かけ上排除体積効果が無視できる温度)のズレが観測される。これらの現象は、輪状高分子鎖のトポロジー的効果によるものと思われる。 これまで多くの人々によって、結び目がほどける(トポロジー的に円となる)確率がランダムウオークのステップ数Nに対してどのように変化するかが、数値計算により調べられてきた。その結果、Nが増えるに従って結び目がほどける確率(P0(N)と書く)は以下のように指数関数的に減少することが分かった。  ここで、N0はランダム結び目が絡まる(非自明な結び目になる)のに必要な特徴的な長さと考えられる。 これまでの仕事では、アレクサンダー多項式 K(t)の特殊値が結び目不量として用いられてきた。この多項式は、プログラム化するのが容易であり、計算時間がN3ですむという長所がある反面、鏡像関係の結び目を区別できないという本質的な欠点を持つ。また、3章で述べるがt=-1以外の特殊値を計算するためには少し面倒な手続きを必要とする。 K(t)の特殊値が結び目不量として用いられてきた。この多項式は、プログラム化するのが容易であり、計算時間がN3ですむという長所がある反面、鏡像関係の結び目を区別できないという本質的な欠点を持つ。また、3章で述べるがt=-1以外の特殊値を計算するためには少し面倒な手続きを必要とする。 K(t=-1)の値は、結び目がほどけるかどうかを判定するには便利な道具であるが結び目の種類を特定することはできない。 K(t=-1)の値は、結び目がほどけるかどうかを判定するには便利な道具であるが結び目の種類を特定することはできない。 ジョーンズ多項式VK(t)は、鏡像の結び目を区別できるなどアレクサンダー多項式にはない優れた長所をもっている。しかし、それはステップ数が増えるに従い計算時間が指数関数的に増大するために、従来は長い結び目の解析には使えないと思われてきた。2章では、著者らによって開発されたジョーンズ多項式を計算するための新しいアルゴリズムを示す。ジョーンズ多項式がVK(t=1)=1となる性質を用いて、ジョーンズ多項式をt=1のまわりで展開したときの展開係数を求めることでこの困難を解決することに成功した。ジョーンズ多項式を1のまわりでテイラー展開すると、  ここで、1次の展開係数は常に0になる。VK(t)が結び目不変量なので、 j(K)も結び目不変量である。展開係数 j(K)も結び目不変量である。展開係数 j(K)がNjの時間で計算できることは、2.3.3章において定性的また数値的に示される。特に2次の微分係数は、アレクサンダー多項式よりも速く計算できる。この不変量は、バッシリエフ不変量と等価であり数学的観点からも大変興味深い。 j(K)がNjの時間で計算できることは、2.3.3章において定性的また数値的に示される。特に2次の微分係数は、アレクサンダー多項式よりも速く計算できる。この不変量は、バッシリエフ不変量と等価であり数学的観点からも大変興味深い。 この 2(K)と 2(K)と K(-1)を組み合わせることによって、ランダム結び目の結び目の型を判定することができる。そのため、P0のみならず結び目の種類を特定した結び目確率を新たに求めることができた。いま、結び目(K)に対する結び目確率をステップ数Nの関数としてPK(N)とかくことにする。結び目の種類Kは、素な結び目として31、41、51、52、素でない結び目として31#31、31#41、31#31#31を選んだ。 K(-1)を組み合わせることによって、ランダム結び目の結び目の型を判定することができる。そのため、P0のみならず結び目の種類を特定した結び目確率を新たに求めることができた。いま、結び目(K)に対する結び目確率をステップ数Nの関数としてPK(N)とかくことにする。結び目の種類Kは、素な結び目として31、41、51、52、素でない結び目として31#31、31#41、31#31#31を選んだ。 4章では、上記のアルゴリズムを用いて理想鎖の(排除体積がない)結び目を解析した。理想鎖の模型として、ガウシアンランダム結び目(3章で説明する)を採用した。30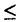 N N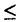 2400の範囲でPK(N)を求めたところ、結び目確率は結び目の種類によらずステップ数が増えるにしたがって滑らかに増加し、あるところで極大に至りそこから急激に減少するという一般形をもつことが分かった。これは、ランダム結び目は始めのうちは非自明な結び目をつくるのには十分な長さを持たないが、徐々に結び目Kができるようになり、ある程度以上ではさらに複雑な結び目ができるためと理解される。著者は、データの解析としてPK(N)に対して以下のような関数を提唱し、非常に良く数値実験の結果と一致することを示した。 2400の範囲でPK(N)を求めたところ、結び目確率は結び目の種類によらずステップ数が増えるにしたがって滑らかに増加し、あるところで極大に至りそこから急激に減少するという一般形をもつことが分かった。これは、ランダム結び目は始めのうちは非自明な結び目をつくるのには十分な長さを持たないが、徐々に結び目Kができるようになり、ある程度以上ではさらに複雑な結び目ができるためと理解される。著者は、データの解析としてPK(N)に対して以下のような関数を提唱し、非常に良く数値実験の結果と一致することを示した。  ここで、CK, K,NKは結び目Kに依存するパラメターで最小自乗法によって決定される。NKを結び目Kに対する特徴的長さと呼ぶことにする。この関数は、自己排除ランダムウオークのスケーリング形から導くことができ、 K,NKは結び目Kに依存するパラメターで最小自乗法によって決定される。NKを結び目Kに対する特徴的長さと呼ぶことにする。この関数は、自己排除ランダムウオークのスケーリング形から導くことができ、 KとNKはそれぞれ臨界指数と見かけ上の隣接格子点数という意味づけがなされる。 KとNKはそれぞれ臨界指数と見かけ上の隣接格子点数という意味づけがなされる。 上記の模型は理想鎖のモデルであるが、現実の高分子では排除体積効果を無視することができない。ランダム結び目に対しても、排除体積効果を取り入れることは現実の高分子を考察する上で重要である。5章では、ロッドビーズ模型を用いて結び目確率の排除体積効果による影響を調べる。これは、結び目の辺の長さは一定で全ての頂点にビーズ(玉)をつけた模型である。ロッドビーズ模型による結び目は、ダイマリゼーションと呼ばれる方法(3章で説明)で生成される。 いま、辺の長さを1としたときのビーズの半径をrとかき排除体積パラメタとよぶ。rの値は、隣のビーズに対しても排除体積の条件を満たすことを要請すると、0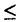 r r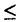 0.5の値をとり得る。KoniarisとMuthukmarは、以前にこのモデルに対してP0(N)の振る舞いを調べ、排除体積パラメタの大きさが0.20を越えるとトポロジー的な絡み合いが非常に少なくなる、つまりN0の値が急激に増えることを指摘した。著者は、この事実を踏まえ(0.20 0.5の値をとり得る。KoniarisとMuthukmarは、以前にこのモデルに対してP0(N)の振る舞いを調べ、排除体積パラメタの大きさが0.20を越えるとトポロジー的な絡み合いが非常に少なくなる、つまりN0の値が急激に増えることを指摘した。著者は、この事実を踏まえ(0.20 r r 0.30)の範囲の排除体積パラメータを特に細かくとり、ほどける結び目だけではなく前述の結び目に対しても結び目確率を求めた。その結果、この領域では排除体積パラメタの僅かな変化に対して、NKの値は結び目の種類に依らず非常に敏感に反応しオーダーが数桁も変化することが分かった。 0.30)の範囲の排除体積パラメータを特に細かくとり、ほどける結び目だけではなく前述の結び目に対しても結び目確率を求めた。その結果、この領域では排除体積パラメタの僅かな変化に対して、NKの値は結び目の種類に依らず非常に敏感に反応しオーダーが数桁も変化することが分かった。 一方、排除体積効果の鎖に対する影響度を測る方法として、末端間距離(Re)のNに対する依存性を調べるのが便利である。末端間距離は、次のようなスケーリング形を持つことが分かつている。  指数 は、臨界指数の一つであり模型の詳細に依らないユニバーサル定数であると考えられている。 は、臨界指数の一つであり模型の詳細に依らないユニバーサル定数であると考えられている。 の値は、理想鎖に対しては1/2であり、摂動鎖(排除体積効果を持つ鎖)では繰り込み群などの解析により0.58…と見積もられている。以上は、漸近極限(N→∞)での話であるが、実際に数値計算をする上ではNが有限であることを考慮しなければいけない。Nが有限でもかなり良い精度で(4)式のような振る舞いがみられる。 の値は、理想鎖に対しては1/2であり、摂動鎖(排除体積効果を持つ鎖)では繰り込み群などの解析により0.58…と見積もられている。以上は、漸近極限(N→∞)での話であるが、実際に数値計算をする上ではNが有限であることを考慮しなければいけない。Nが有限でもかなり良い精度で(4)式のような振る舞いがみられる。  Nが有限のときの指数 effを有効指数と呼ぶことにする。 effを有効指数と呼ぶことにする。 effの値は排除体積パラメタが十分大きいとき(例えば格子上の自己排除的ランダムウオーク)は10ステップ程でかなり良い漸近値 effの値は排除体積パラメタが十分大きいとき(例えば格子上の自己排除的ランダムウオーク)は10ステップ程でかなり良い漸近値 をとるが、排除体積パラメターが小さい場合にはやや をとるが、排除体積パラメターが小さい場合にはやや よりも小さい値をとる。このことは、一見繰り込み群の固定点が1つしかないことと矛盾するようであるが、 よりも小さい値をとる。このことは、一見繰り込み群の固定点が1つしかないことと矛盾するようであるが、 effはNが大きくなるに従って徐々に effはNが大きくなるに従って徐々に に近づくと考えることができる。しかし、この変化は非常にゆっくりしており、解析した範囲(0<N<3000)ではほぼ一定値とみなしてよい。この値を有効指数( に近づくと考えることができる。しかし、この変化は非常にゆっくりしており、解析した範囲(0<N<3000)ではほぼ一定値とみなしてよい。この値を有効指数( eff)と呼ぶ。著者は、摂動鎖に対するもう1つの有効指数として3章で定義される eff)と呼ぶ。著者は、摂動鎖に対するもう1つの有効指数として3章で定義される effも調べた。 effも調べた。 有効指数 effと effと effを、各々の排除体積パラメタに対して求めると大変興味深い事実が分かった。それは、NKの値が急激に増大するときと、2つの有効指数が漸近値をとるときのrの値はほぼ同じであるということである。これは、有効指数が結び目確率を調べる上で非常に有用な指標となることを示している。 effを、各々の排除体積パラメタに対して求めると大変興味深い事実が分かった。それは、NKの値が急激に増大するときと、2つの有効指数が漸近値をとるときのrの値はほぼ同じであるということである。これは、有効指数が結び目確率を調べる上で非常に有用な指標となることを示している。 次に、(3)式中のパラメタ( K,NK)の結び目依存性に関して述べる。まず、NKの値は結び目種類に依らず、ほぼ同じ値であった。また、 K,NK)の結び目依存性に関して述べる。まず、NKの値は結び目種類に依らず、ほぼ同じ値であった。また、 Kについては、素でない結び目の Kについては、素でない結び目の Kの値はその成分である結び目の値のほぼ足し算になっている、結び目の種類には依存するが排除体積パラメタにあまり依存しないという傾向がみられる。これらのことは、4.3章と5.2章の結果からみてとれる。 Kの値はその成分である結び目の値のほぼ足し算になっている、結び目の種類には依存するが排除体積パラメタにあまり依存しないという傾向がみられる。これらのことは、4.3章と5.2章の結果からみてとれる。 6章では、結び目の種類を特定したときの慣性半径の振る舞いが調べられる。この研究は、先に紹介した環状DNAの電気泳動の実験との関連が深い。著者は、ランダムウオークの漸近形から次のような関数を仮定した。  数値計算の結果をみる限りでは、結び目の種類による違いは、小さいステップ数の時には顕著な違いが認められるが、漸近領域では違いは僅かで指数 Kの値は全て一致すると思われる。このことより、長い高分子の慣性半径にはトポロジーの制限はあまり影響しないことが示唆される。 Kの値は全て一致すると思われる。このことより、長い高分子の慣性半径にはトポロジーの制限はあまり影響しないことが示唆される。 最後に7章で、得られた結果をまとめ、ランダム結び目の応用について述べる。 本論文では、ランダム結び目に対する新たな解析法を開発し、結び目確率、排除体積効果、末端間距離等に対して新しい結果を提出した。これらの成果は、ランダム結び目という分野の確立に寄与するとともに、高分子のみならず多くの1次元物体のトポロジー的解析に有用な知見を与える。 |