非線形偏微分方程式の解を議論する事が大変困難である事はよく知られている。しかし、その1分野をなすソリトン方程式の研究は我々に大変興味ある結果を与えてきた。ソリトン方程式の持つ特徴として、安定な孤立波解を持つ事が挙げられる。幾つかの孤立波が衝突したとしても、発散あるいは崩壊しないばかりでなく、はじめの孤立波の情報を大変よく保持した孤立波が伝播する事が知られている。更に、方程式によっては、初期値問題すら解く事が出来るというのは、驚きに値する。現在、数多くのソリトン方程式が知られているが、その多くは1+1次元の方程式である。従って、1+1次元のソリトン方程式の解析的手法は、よく研究されている。

　1974年、A.DaveyとK.Stewartsonは、2次元の水面波を記述する方程式として、Davey-Stewartson(DS)方程式を提出した。この方程式もソリトン方程式として知られており、1+1次元でのnonlinear Schrodinger(NLS)方程式に対応する。DS方程式は、2次元的に局在した解を持ち方程式も空間的に対称となっている事から2+1次元ソリトン方程式のモデル方程式として重要な地位を占めている。幾つかの1+1次元ソリトン方程式はAKNS形式のLax方程式として導かれる事が知られている。DS方程式は、このAKNS形式を2次元化する事によって導かれる。この事は、DS方程式は、更なる高次元化を期待できる方程式であることを示す。従って、DS方程式の構造を調べる事は、2+1次元の問題に留まらず、高次元のソリトン方程式の研究の基礎となるものと考える。方程式の構造を調べるためには、その方程式を含むclassを考える事が、1つの手段である。このことから、著者は本論文でDS方程式系について論ずる。

　DS方程式は放物型のDS1方程式と双曲型のDS2方程式に分類される。DS1方程式は、積分境界値として、2つの任意の実数関数を含んでいる。従って、DS1方程式はDS2方程式に比べ多様な解を持つ。本論文では、DS方程式系について、以下の事を議論する。

　1.新しい線形補助方程式系の提案。

　2.高次のDS方程式の導出。

　3.逆散乱法による、高次のDS1方程式の解析。

　4.DS1方程式系がもつ解の導出とその解の漸近的振舞。

　著者は以前に、1975年にM.J.AblowitzとR.Habermanが発見した線形補助方程式系を用いて、高次のDS1方程式を導いた。そこでは、高次のDS1方程式も、ある変数変換によって、空間変数に対して対称な方程式になることをみた。著者は、DS1方程式系を調べるためには、補助方程式は、空間変数に対して対称に記述されることが必要と考えた。この考えにより、DS方程式系を記述する新しい補助方程式を提案した。

　ここで、₃＝diag(1,-1)、そして、つぎの略記を使った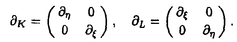

　本論文全体にわたり、大文字Nは、方程式の次数を表す事とし、また、DS1方程式系の解qの境界条件は無限遠でゼロとする。

　第2章では、DS1方程式(N＝1)の場合のを書き下し、1990年の、A.S.FokasとP.M.Santiniの逆散乱法による解析を参考に、線形補助方程式(1)の解析を行った。DS1方程式系特有の方程式(1a)式を、逆散乱法を用いて解析すれば、解q(,,t)は未知のベクトル関数x(,t),y(,t)を用いて表現される事が分かる。さらに、振幅│q│²が保存密度となっていることを示す事が出来る。この解qの時間発展(つまりx(,t),y(,t)の時間発展)は、式(1b)によって決定される。ところが、特殊なJost関数の境界条件を用いてqの表現を得たために、解qの時間発展を矛盾なく得るためには、式(1b)を変形する必要がある。式(1b)に、ある項を加える事で、この問題は解決される。この様にして、qの時間発展は、時間に依存するSchrodinger方程式

　を解く事によって得られる事が分かる。

　DS1方程式特有の特解として、興味ある性質をもつ解がある。式(2)において、u＝²x²と仮定して、調和振動子解を構成する事が出来る。それを用いて、我々は、調和振動子のように振動するDS1方程式の特解を求めた。

　第3章では、高次のDS1方程式を体系的に導く方法、および、解qの時間発展について議論する。第2章で、Jost関数(,,t;k)がk→∞の時、kの逆巾で展開される事を示した。この性質を用いて、を決定する事ができる。しかし、そこで、が未定関数を含む事が分かる。DS1方程式中の積分境界値が実数関数であるように、これら未定関数に制限を負わせることを考えなければならない。そのために、DS1方程式系は保存密度|q|²を持つという性質を利用する。この様にして、DS1方程式系は次の様に記述される事が分かった

　ここで、、は、ある実数関数である。例として、2次及び、3次(N＝2,3)のDS1方程式を導いた。2次のDS1方程式は、変形KdV方程式の2次元版として知られているNizhnik-Veselov-Novikov(NVN)方程式を、複素的に拡張した方程式である。また、DS2方程式系は、変換→z,→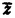によって得られる。

　DS1方程式の場合と同様に、高次のDS1方程式の解の時間発展を議論するためには、相当する方程式(1b)を適当に変形する。(2)式に対応して、線形化及び1次元化されたN次のDS1方程式

　を解けばよい事を得た。ここで、は積分境界値,に対応する。

　第4章では、DS1方程式系を満足するある解の類を考え、更にその解の漸近的振舞を考察した。1988年に、M.Boitiらは、Backlund変換を用いてDS1方程式の2次元的に局在した解(ドロミオン)を発見している。本章では、ドロミオン解の類について議論する。まず、(3)式と方程式

　を結びつけるDarboux変換を発見した。そのとき、は、実数関数となることを示した。又、を体系的に導く方法を発見した。この様にして、N次DS1方程式のドロミオン解と、それを生成する関数,を求める事ができる。N＝1の時、このドロミオン解は、A.S.FokasとP.M.SantiniがDS1方程式の解として導いた(L,M)ドロミオンとほぼ同じものである。次に、このドロミオン解qに対して、代数的計算を用いて、各ドロミオンが十分離れている時の漸近的性質(各ドロミオンの極大値、その位置、衝突による位置のずれ)を調べた。その結果から、幾つかの興味ある性質をみる事が出来る。まず、ドロミオンの衝突による位置のずれは各ドロミオンの配置に依存するということを発見した。また、ドロミオンは、衝突によって消滅する、あるいは、新たに生成される可能性があるということを確かめた。特に、(2,2)ドロミオンに対して、これらのことを明確に示した。最後に、このドロミオンが摂動をうけると、大変複雑な振動を伴うドロミオンが伝播する事を示した。

　本論文では、DS方程式系に含まれる方程式達、及びそれらの解について論じた。ここで与えた手法は、DS方程式系以外の方程式系にも利用できる。2+1次元ソリトン方程式は、一般に積分境界値として任意関数を含む。従って、散乱データーの時間発展方程式は任意関数に依存する。よって、1+1次元ソリトン方程式での初期値問題は、2+1次元では初期値境界値問題に対応する。そして、2+1次元ソリトン方程式系の解の類を求めるには、この境界値に対応する任意関数がどの様な関数で与えられるかを見出す必要がある。著者は、解の類(及び、境界値に対応する任意関数)を発見するための一つの方法を与えた。更に、方程式系について議論するには、保存密度を利用する事が有効な手段である事を示した。この様に、著者は、2+1次元ソリトン方程式系の構造を調べるための一般的手法を与えた。

　学位申請者は、2次元の非線形方程式として知られているデイビー・スチュワートソン方程式(以下に、DS方程式と略記)に着目し、ひとつの特解としてリサジュー図形を描きながら進む局在した解を見いだすとともに、DS方程式の拡張として新しい線形補助方程式を提唱し、高次の分散関係を持つDS方程式系を導出した。また、得られたDS方程式系の解の類として、もとのDS方程式と同様の局在解(ドロミオン解)およびこの様な解を保証する境界関数を、任意次数の分散の場合に系統的に求めることに成功した。さらに、得られた解の漸近的性質を解析的に調べることにより、いくつかの興味ある新しい結果を得た。

　デイビー・スチュワートソン方程式は、水面の波およびプラズマ中の電荷分布を記述する方程式として物理的に興味深いのみならず、2+1次元の非線形方程式のうちでソリトン解を持つ希有な例として、数学的にも強い関心を集めている。DS方程式は、2次の分散関係を持つが、その符号が正である放物型のDSI方程式と、負の双曲型のDSII方程式に分類される。このうちDSI方程式は、積分境界値として二つの任意の実関数を含むために、初期値境界値問題として多様な解を持つと期待される。申請者によって議論された事柄は、次の通りである。