現在、最も精度の高い音場の予測手法は模型実験法、特に1/10スケールモデルを用いる方法である。しかし1/10スケールモデルは、製作に際し多大な時間と費用を要する、また度重なる変更に対して対応しにくいという欠点をもち、より小型の模型を用いた予測手法が模索されている。 一方で、近年のコンピュータの発達を背景に、音響の分野においても、コンピュータを用いた数値シミュレーションが盛んに研究されている。 しかしながら、波動方程式は双曲型偏微分方程式の中では最も単純な形の方程式の1つであるにもかかわらず、波動方程式の数値計算による音場解析は未だ建築音響の現場で十分活用されているとは言いがたい。 本研究は、波動方程式を基礎式として、室内などの過渡音場を差分法を用いて数値解析する方法について、理論的考察、実験ならびに数値実験によって検討を行ったものである。 本論文の概要を以下に示す。 序章において、本研究では、従来よく行われており音場を計算する際に巨大なマトリクス演算に帰結されるHelmholtz方程式を基礎式として定常問題として取り扱う方法を用いないこと、この方法に代わるものとして、波動方程式を陽型差分法によって定式化し、インパルス応答を直接もとめる数値解析法を採用する理由について説明した。次に、関連する既往の研究について述べた。 第1章では波動方程式に基づき音場をモデル化するための検討を行った。 特にインパルス応答の計算モデルを導出するために、長方形音場に対する境界積分方程式をFourier展開することによりいくつかの解析解を求めた。得られた解析解を2次元音場の実験結果と比較することにより、初期音圧分布を与えるモデルが適当であることを示した。 また実用上、無限に高い周波数まで必要とせずある周波数以下の応答を得る場合には、有限の初期振幅をもつパルス形初期条件を用いることができる。このようなパルス形初期条件の中で、得られる解の形が最も単純となる直方体形パルス状の初期音圧分布モデルが実験結果とよく対応していることを示した。以上から、インパルス応答を表す計算モデルとして、直方体形パルス状の初期音圧分布モデルが適当であると結論づけた。 第2章では差分法による離散化とサンプリング定理との間に直接の関係のないことを2つの例を用いて説明した。 また、波動方程式が双曲型であることによる不連続性の伝播という性質によって、差分法を用いて不連続性を含む問題を解く場合には数値振動の発生が避けられないことを数値実験により指摘した。 さらにその数値振動を低減するための3種類の手法を提案した。これらの詳細については、第3章から第5章において詳述した。 第3章では、不連続性の伝播によって生ずる数値振動の3つの低減手法のうち、1つめの手法である不連続性を含む問題を滑らかな計算モデルに変換するという手法について説明した。 この手法は、初期条件に起因する数値振動を低減するためには最も単純で扱いやすい手法である。滑らかな初期条件を与えることによって数値振動の発生は抑えることができるものの、滑らかな数学モデルを精度よく記述するために分割グリッドを細かくする必要があり、結果として、最大数千倍もの計算機の記憶容量が必要となることを述べた。また、記憶容量必要量の増大と同程度の計算時間の増大が予想されることを指摘した。 さらには、直接音が初めに境界に反射するまでの時間の数値解を解析解で置き換えるという手法を提案し、この手法のもつ以下の3つの利点について説明した。 ○ 比較的高周波数帯域まで計算する等、大規模な差分格子を用いる場合、計算時間の短縮が見込まれる。 ○ 無反射時間領域分の数値誤差の累積を回避できる。 ○ 差分解における初期値の記述精度を高めることができる。 あるいは、同程度の精度の数値解を得るための差分格子数を減少させることができる。 第4章では、数値振動の低減手法のうち2つめの、差分スキームに人工粘性を付加するという手法について説明した。初めに、人工粘性について説明し、次に数値実験により2次の空間微分誤差である人工粘性が数値振動をある程度低減し、その結果数値解において反射音位置がわずかに確認できる程度になることを示した。 また、スタガードメッシュ上において、特にパルス性の初期条件を設定する場合、モデル化誤差を生じさせないために注意すべき点について整理した。 第5章では、数値振動の低減手法のうち3つめの、双曲型方程式において不連続性が伝播する軌跡の集まりである特性曲面を用いて計算を行う手法(特性曲面法)について説明した。初めに、特性曲線法について説明し、線形である1次元の波動方程式を特性曲線法によって解く場合、一般の準線形偏微分方程式を特性曲面法により解く場合に比べて手続きが単純化されることを示した。また、この手法が通常の差分スキームの1つであるFriedrichsスキームのCourant数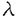 =1の場合に相当することを示した。 =1の場合に相当することを示した。 次に、多次元における特性超曲面法について説明し、数種類ある特性曲面法のうち固定した特性曲面を用いないButlerの手法に基づき2次元の波動方程式を離散化した。 また3次元においては、一般には特性超曲面法を展開することは極めて困難であることを述べる一方で、線形である3次元の波動方程式に限定することにより、2次元における手法を拡張して特性関係式を導出した。 第6章では、同一のモデルをいくつかの差分スキームを用いて解き、解析解・実験結果と比較することで、現時点での精度の高い計算手法を追究した。 はじめに、1次元では滑らかな問題と不連続性を有する問題に対して、分割数の増加に従って解析解に対する精度が向上することを定量的に示した。また同じ分割数では滑らかな問題の法が不連続性を含む問題より精度が高くなることを示した。 2次元においては、長方形音場を対象とし、以下の4種の差分手法で解析し、解析解・実験結果との比較を行った。 ・Courant-Friedrichs-Lewyスキーム Gaussパルス形初期条件(滑らかな問題) ・Courant-Friedrichs-Lewyスキーム 直方体パルス形初期条件(不連続性を含む問題) ・Leap-frogスキーム 直方体パルス形初期条件 ・特性曲面法中央差分スキーム 直方体パルス形初期条件 この結果からGaussパルス形初期条件をもつCourant-Friedrichs-Lewyスキームが最も精度よく解析できることを確認した。 直方体パルス形初期条件をもつCourant-Friedrichs-Lewyスキームはグリッドを細分化しても、精度の向上が見込まれないことを確認した。 直方体パルス形初期条件をもつLeap-frogスキームではメッシュを細分化することで人工粘性の効果が高まり、数値振動がわずかに抑えられるものの、期待できるほどの精度は得られなかった。 直方体パルス形初期条件をもつ特性曲面法中央差分スキームの場合は、数値振動が強く抑えられ、大きな反射音構造が確認できるようになったものの、本論文の差分スキームでは人工粘性が強すぎて応答の変動まで抑えられる結果となり、実用性に乏しいことが判った。ただし、特性超曲面法の可能性は示されたと考えている。 3次元においては、2次元における検討の結果を受けて、Gaussパルス形初期条件をもつCourant-Friedrichs-Lewyスキームを用いて、直方体音場を解析した。また、2次元と同様に、解析解と実験結果との比較を行った。 3次元での計算は大規模となるため、本研究では十分に高い周波数帯域まで計算することができなかったが、1/5残響箱に相当する1.58m×1.16m×0.96mの大きさの空間に対しておよそ4kHzまで計算することができた。実験結果および解析解と比較することで、数値解において必要とされる精度は得られているものと考えた。この計算に対して、パーソナルコンピュータを用いて、10msの時間応答を得るのに、約1時間を要した。また、コンピュータメモリ要求量は15Mbyte程である。 第7章では、各章における検討結果取りまとめた。 特に第6章の結果から、例えば3.0m×4.0m×2.5mの大きさの居室を2kHzまで計算するのに要するコンピュータの記憶容量および計算時間は以下のように概算される。 コンピュータ記憶容量:32Mbyte 計算時間:27時間(0〜100msまで計算) 上の概算例から、居住空間の音場計算を行うという目的に対して規模の小さな空間では実用可能なレベルに達していることを示すことができた。 また、近い将来に大規模なメモリ空間をもつ高速のコンピュータを用いることで、大きな音場を比較的高い周波数まで計算できる可能性があると考えた。 Appendixには、数値解の精度を検討するための非定常解析解を導出している。 本論文を通じて、波動方程式を陽型差分スキームを用いて数値解析するという手法を採用することで比較的規模の大きな音場のインパルス応答を高い周波数まで計算できる可能性が示された。これを実現する手法として、現時点では滑らかな初期条件を設定することが最も有効な手法である。また特性超曲面法の可能性も確認できた。滑らかなパルス形初期条件を用いる場合、不連続性を含む初期条件と比較してコンピュータの記憶容量および計算時間が増大してしまうため、特性超曲面法の改良が期待される。 |