| 内容要旨 | | 本研究の目的は非圧縮性固体,特にゴム材料などの極限的な大変形解析に適した信頼性の高い有限要素の開発を行なっていくうえでの指針を明確化することにある. 現在,線形・非線形解析を問わず有限要素法により非圧縮性固体・流体や板・シェルの解析を精度良く行なうためには混合変分原理を用いることが不可欠であるとの認識が定着しつつある.非圧縮性固体を例にとれば,通常の有限要素法は独立な未知量として変位のみを用いるのに対し,混合型有限要素法では変位に加え,圧力なども独立な未知量として定式化を行なう点に特徴がある.しかしながら変位と圧力2つの場の有限要素近似を行なう補間関数の組み合わせが悪いと,場合によっては解の精度が著しく低下することが知られており,これは一般にロッキング現象とよばれている. ロッキングとは,数学的には解の離散化による誤差の最適収束性が満たされていないことを意味しており,最適収束性の十分条件として,線形の範囲では離散化LBB条件が知られている.LBB条件(Ladyzhenskaya-Babuska-Brezzi condition)とは,線形の範囲において離散化する以前の混合変分原理の解の唯一存在性及び安定性のための必要十分条件であり,それを有限要素離散化を行なったものが離散化LBB条件である.まず,非圧縮性線形弾性体を例に,一般的な抽象的パラメータ依存型問題に関する解の安定性の条件がLBB条件により与えられること,また混合型要素がロッキングを起こさないための為の条件が離散化LBB条件によって与えられることを示す. 線形弾性体の場合有限要素法の基礎式となる仮想仕事の原理の式は以下のように表わされる. (V)与えられた外力fに対し以下の条件を満たすu∈Vを求めよ  ただし系が占める領域を 境界を∂ 境界を∂ ,変位許容関数全体の集合をVとし.fは体積力, ,変位許容関数全体の集合をVとし.fは体積力, は体積弾性係数, は体積弾性係数,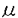 は剪断弾性係数, は剪断弾性係数, Dijは偏差ひずみである.よく知られているように式(1)をそのまま変位法により離散化を行なうと Dijは偏差ひずみである.よく知られているように式(1)をそのまま変位法により離散化を行なうと の増加に従って解の誤差が著しく増大するため混合法を導入する.式(1)に対応する混合法としては以下に示すMixed interpolation with projection(以下,射影混合法)が知られる.Vとは異なる許容関数の空間Qをとり,式(3)にのように定義された の増加に従って解の誤差が著しく増大するため混合法を導入する.式(1)に対応する混合法としては以下に示すMixed interpolation with projection(以下,射影混合法)が知られる.Vとは異なる許容関数の空間Qをとり,式(3)にのように定義された (div u)のQへの正射影をpとして(V)を書き直すと(V×Q)をV,Qの直積として,以下の混合型変分問題が得られる. (div u)のQへの正射影をpとして(V)を書き直すと(V×Q)をV,Qの直積として,以下の混合型変分問題が得られる. (M)与えられた外力fに対し以下の条件を満たす(u,p)∈(V×Q)を求めよ  この混合変分原理の合理性は(M)が任意の外力fに対し唯一解(u,p)∈(V×Q)が存在し,かつ安定である事により保証される.但し安定性とは一般に外力fに対する解(u,p)が得られたとき外力の多少の変動により解(u,p)も有限な変動しかしないことであり,f+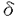 fに対する解が(u+ fに対する解が(u+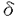 u,p+ u,p+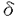 p)であったとき(4-a)を満たす正定数C>0が存在することであると定義されるが,ここでは線形問題のみを考えているので任意の外力fに対して式(4-a)が成立するためには,式(4-b)が成立することが必要十分条件となる.以下では式(4-b)を安定性の定義として用いる. p)であったとき(4-a)を満たす正定数C>0が存在することであると定義されるが,ここでは線形問題のみを考えているので任意の外力fに対して式(4-a)が成立するためには,式(4-b)が成立することが必要十分条件となる.以下では式(4-b)を安定性の定義として用いる.  の形式のマトリックス方程式にすることができるが,混合変分原理を用いて定式化を行なうものであれば,基本的にこれと同じ形式のマトリックス方程式が得られる.このことからも類推できるように,混合変分原理を用いているものであれば本質的に同じ議論により解の唯一存在性・安定性の条件を導くことができる.式(2)に対応してa(u,v),b(v,q),F(v)を以下のように定義する.  以上の表記法を用いれば,(M)は以下のような一般的なパラメータ依存型問題として記述できる. (P)与えられたF∈V*,G∈Q*, ∈[0,E0]に対し以下の条件を満たす(u,p)∈V×Qを求めよ ∈[0,E0]に対し以下の条件を満たす(u,p)∈V×Qを求めよ  ここでV*,Q*はそれぞれV,Qの相対空間, ∈[0, ∈[0, 0]はパラメータで,非圧縮性固体の場合は 0]はパラメータで,非圧縮性固体の場合は =l/ =l/ である,またこの場合G(q) である,またこの場合G(q) 0であるが板やシェルの場合はそのかぎりではないので表現に一般性を持たせるためにこのようにする.関数解析の諸定理を用いることにより,(P)が任意のF∈V*,G∈Q*, 0であるが板やシェルの場合はそのかぎりではないので表現に一般性を持たせるためにこのようにする.関数解析の諸定理を用いることにより,(P)が任意のF∈V*,G∈Q*, ∈[0, ∈[0, 0]に対し唯一解を持ち安定であるための必要十分条件は, 0]に対し唯一解を持ち安定であるための必要十分条件は,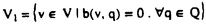 として,以下に示すような(D1)(V1-elliptic(楕円性)),(D2)(LBB条件(Ladyszhenskaya-Babuska-Brezzi conditionであることが証明できる. として,以下に示すような(D1)(V1-elliptic(楕円性)),(D2)(LBB条件(Ladyszhenskaya-Babuska-Brezzi conditionであることが証明できる.  通常の方法で有限要素近似を行なうことは数学的には前述の許容関数の空間V,Qの有限次元部部空間を構成することを意味しており,ある要素分割を決めると要素の長さを代表するメッシュパラメータをhとして離散化された許容関数全体の空間Vh,Qhが定義でき,以下のような離散化問題が得られる. (D)与えられたF∈V*,G∈Q*, ∈[0, ∈[0, 0]に対し以下の条件を満たす(uh,ph)を求めよ 0]に対し以下の条件を満たす(uh,ph)を求めよ  前節と同様に(D)が唯一解を持ちかつ安定であるための条件は(D1),(D2)に対応しVhl=X(Bh)として  となる.任意の要素分割に対し要素の細分化によらず hが有限の値を取ること即ち hが有限の値を取ること即ち を離散化LBB条件と言う.このとき安定性の条件により を離散化LBB条件と言う.このとき安定性の条件により  が任意のhについて成立している.またこれを用いれば連続問題(P)の解を(u,p),離散問題(D)の解を(uh,ph)としてメッシュサイズhに依存しない正定数C>0に対し 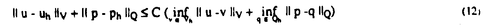 が成立することが証明できる.左辺は正解と有限要素近似解の誤差,右辺はその時の有限要素空間の近似〓力を表わしている.この不等式は誤差の最適性の条件と呼ばれロッキングを起こしていない条件である.従って離散化LBB条件はパラメータ依存型混合変分問題の解の誤差の最適収束の為の必要条件にもなっている. 以上により混合型有限要素法有効性のためには(D1’),(D2’)の成立が必要である.ここでは特に証明が困難な(D2’)即ち離散化LBB条件の数値的予測法について述べる.(D2’)のノルムのマトリックス表示を  とし,式(14)の固有値問題の非零の固有値を大きさの順に と並べれば,特異値解析により と並べれば,特異値解析により となることが証明できる.また同様な固有値問題式(15)の非零の固有値を大きさの順に となることが証明できる.また同様な固有値問題式(15)の非零の固有値を大きさの順に とすれば とすれば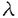 i= i=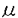 iとなっていることが証明できる. iとなっていることが証明できる. 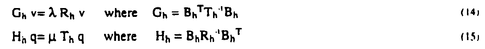 離散化LBB条件は にほかならないから,数種類のメッシュ分割に対して(14)あるいは(15)の固有値解析を行ない,メッシュの細分化に伴うメッシュパラメーターの減少に にほかならないから,数種類のメッシュ分割に対して(14)あるいは(15)の固有値解析を行ない,メッシュの細分化に伴うメッシュパラメーターの減少に hが依存するが否かを調べ,hと共に減少していく傾向にあるものはLBB条件をみたさない,逆にhに依存せず有限の値に〓してく傾向にあるものはLBB条件をみたす"と予測する. hが依存するが否かを調べ,hと共に減少していく傾向にあるものはLBB条件をみたさない,逆にhに依存せず有限の値に〓してく傾向にあるものはLBB条件をみたす"と予測する. 2次元4角形要素の判定結果を表1に示す.表中で名称の下に2段にわたりpass/failと示してまるのは中段かっこ内が解析的な結果が知られているものについてはその結果,下段は本解析による判定結果である.解析的な結果と本研究による数値的な予測は極めてよく一致している事がわかる.このほかに実際に現在よく用いられているほとんどの2次元3角形,3次元4面体,6面体要素を含む各種連続体要素について系統的に調査を行ない,解析的な結果と比較することにより,この手法の妥当性を確認し,結果を整理した.  表1 4角形要素の結果 表1 4角形要素の結果 つぎにゴム材料のモデル化に適している超弾性体の混合型有限要素解析について考察する. 超弾性体はゴムなどの高分子材料の変形挙動をよく表す物質モデルとして知られており,式(16-a.b)に示すように,変形や歪みの成分で微分することにより共役な応力成分を生じるような弾性ポテンシャル関数Wが存在する物質として定義される.   ,Sは第1,2Piola-Kirchhoff応力テンソルでTをCauchy応力テンソル,Fを変形勾配テンソルとして ,Sは第1,2Piola-Kirchhoff応力テンソルでTをCauchy応力テンソル,Fを変形勾配テンソルとして  と定義される.また,C=FT・Fは右Cauchy-green変形テンソル,E=(C-I)/2は,Green-Lagrangeひずみテンソルである.本研究では代表的な超弾性体のポテンシャルとして知られているMooney-Rivlin体  及びMooney-Rivlin体に高次項を付加したモデルを用いる.  ここで,IC,IIC,IIICはCの主不変量である. 次に超弾性体のポテンシャルを元に非圧縮性混合型有限要素法を導く,非線形問題に対し非圧縮性の拘束を考慮する方法には様々なものがあるが,これまで一定の成果を上げてきたものにはLagrange未定乗数法とペナルティ法がある.それぞれの基礎式は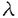 をLagrange未定乗数, をLagrange未定乗数, をペナルティ係数とし,以下のように拘束のためポテンシャルを加えた全ポテンシャルに対し停留ポテンシャルエネルギーの原理を適用し導く. をペナルティ係数とし,以下のように拘束のためポテンシャルを加えた全ポテンシャルに対し停留ポテンシャルエネルギーの原理を適用し導く.  ただし,tは表面力ベクトル,gは体積力ベクトルで,簡単のためdead loadとする.またWV(IIIC)はIIIC=1でWV=0,∂W2/∂IIIC=1となるような関数である. 次に以上2種類の方法を包括する射影混合法を導き,それらの関係を考察する.射影混合法では,まず変位の許容関数の空間Vとは別の関数空間を定め. WVのQへの正射影を WVのQへの正射影を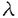 とする.即ち とする.即ち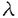 は, は,  を満たすものである. WVを WVを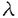 に対応させる作用素をPとする.即ち,P( に対応させる作用素をPとする.即ち,P( WV)= WV)=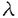 である.この作用素Pを用いて,式(21)により定義されるペナルティ法の全ポテンシャルを式(23)のように修正し,停留ポテンシャルエネルギーの原理及び射影の定義式(22)を用いると式(24),(25)に示すような射影混合法の基礎式が得られる. である.この作用素Pを用いて,式(21)により定義されるペナルティ法の全ポテンシャルを式(23)のように修正し,停留ポテンシャルエネルギーの原理及び射影の定義式(22)を用いると式(24),(25)に示すような射影混合法の基礎式が得られる.  この射影混合法とペナルティ法との関係は,前述のとおりペナルティ項に何らかの操作を加えたものになっている.また,Lagrange未定乗数法との関係も式の形から明かで,射影混合法で, →∞とすれば,そのままLagrange未定乗数法の基礎式が得られる. →∞とすれば,そのままLagrange未定乗数法の基礎式が得られる. 以上の定式化により得られた非線形問題の信頼性について検討する.まずどのような非線形問題であっても変形が微少な範囲内では線形問題と考えることができ,従って前述したLBB条件を満たさない要素は信頼性は低いと言える.しかしながら線形問題で信頼性があるからといって,非線形問題で信頼性が確認できたわけではなく,非線形問題についての信頼性に関する議論を行なう必要がある.しかしながら非線形問題については先のLBB条件のような明確なものがない.そこで混合型有限要素法により基礎的な例題(片側固定ブロック,純粋せん断,ブロック圧縮など)を実際に解析を行なうことにより,各種要素の比較検討を行ない以下のような知見を得た.まずLBB条件を満たさない要素は得られた圧力解が不合理な振動を起こすなど解の信頼性が低いことを確認した.またLBB条件を満たす要素についても拘束関数と境界条件に対応して不合理に変位が振動した解が得られる場合があることがわかった.ここで行なった範囲では4角形要素では変位はLagrange族の9節点で,圧力は要素内線形分布の要素が,3角形要素では変位はLagrange族の6節点にbubble関数を付加したもので,圧力は要素内線形分布の要素が良好な結果が得られた. 最後にこれまでの議論の結果を実際の問題に応用した解析例として,捩じりを受けるロッドの3次元大変形において観測される"kinking"と呼ばれる力学的に興味深い現象が有限要素法によってシミュレートできる事を示し,kinkingの力学的特徴を示す.解析には1辺が1の正方形断面で長さが20のロッドを用いる. まず下端は固定,上端は初期の正方形の形状を維持したまま360度の捩じりを与えた後,軸方向に圧縮を行なった.このときの圧縮率に対する上端面の捩じりモーメントの関係を図1 path Aに,また,変形図を図2 path Aに示す.Path A圧縮率約0.67で3次元変形から2次元変形へのモードの遷移し輪を生じることにより,捩じりモーメントは完全に0になり,曲げのみの変形になる.次にこの輪を引き伸ばすと,図2 path Bに示すように変形が1箇所に押し込められたこぶが発生する.この時の上端面の捩じりモーメントは図1にpath Bとして示すように0のままである.このように,こぶの発生により捩じりモーメントが解放されることがkinkingの特徴である. 次に以上のようなシミュレーションを初期の捩じり角を種々変化させて行なった.まず初期捩じり角が1回転未満の場合はこぶを発生するような変形は現われない.初期捩じり角が1回転以上の場合の例として,図3(a)に初期捩じり角が2回転の場合の変形図を示す.但しここではロッドを上下端間隔を固定したまま捩じった状態(状態0)から真直なままひきのばし,分岐点(状態1)で分岐解析を行ない適当な捩じり座屈経路に誘導し,それから圧縮を行なっている.図中の状態2とはRiks法によって解析を進めた場合,到達できる最大の圧縮率に於ける変形で,その後変形は伸びる方向へと転じ,それまでとは異なる変形モードで進行し,最終的に圧縮率が0の時点で図3(a)の最後の変形図に示されるこぶを発生する(状態3).以上の変形は2回転以上の初期捩じり角のケースでも基本的に同じになる.参考までに図3(b)に初期捩じり角が5回転の場合の状態3の変形図を示す.図4に1回転以上の初期捩じり角のロッドについて,状態1から状態2を経て状態3に至る過程における圧縮率と,上端面の捩じりモーメントの関係,図5に各ケースの初期捩じり角に対する状態0と状態3での捩じりモーメントの関係を示す.図5からこぶの発生はそれぞれ約1回転分の捩じりモーメントを解放していることがわかる.状態0を結んだ点線と,状態3を結んだ点線が完全な平行線にならないのは,このロッドの断面が矩形であることや,長さに対して断面の寸法が無視できないためだと考えられる.また初期捩じり角が6回転のものは,最大圧縮率が負の値になり,状態0から1、2を経てもとの長さに至る連続な経路が存在しないため状態3が定義できない.以上のことから,図5中に示すように,初期捩じり角について,kinkingを生じることのないnon-kinking領域,有限な圧縮を与えない限りこぶは発生しないという意味でのtransition領域,圧縮の必要のないkinking領域に分類することが可能であると考えられる. 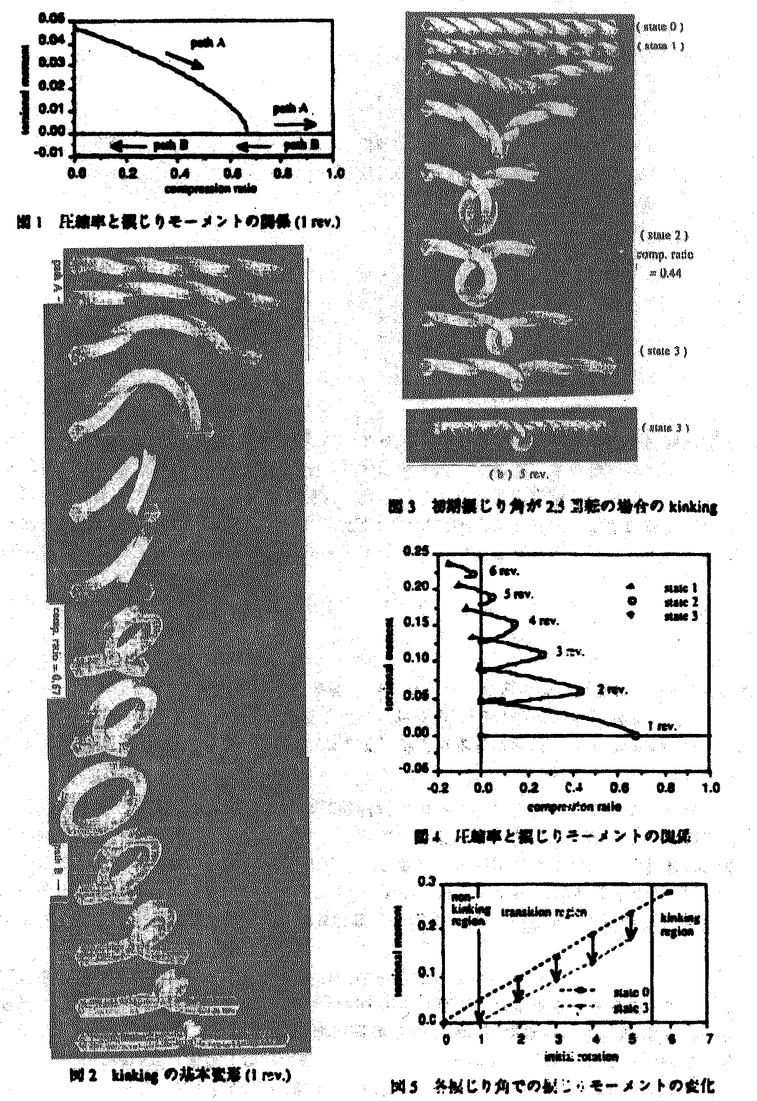 図表図1 圧縮率と捩じりモーメントの関係(1 rev.) / 図2 kinkingの基本変形(1 rev.) / 図3 初期捩じり角が2.5回転の場合のkinking / 図4 圧縮率と捩じりモーメントの関係 / 図5 各捩じり角での捩じりモーメントの変化 図表図1 圧縮率と捩じりモーメントの関係(1 rev.) / 図2 kinkingの基本変形(1 rev.) / 図3 初期捩じり角が2.5回転の場合のkinking / 図4 圧縮率と捩じりモーメントの関係 / 図5 各捩じり角での捩じりモーメントの変化 |
| 審査要旨 | | 本論文は,「非圧縮性超弾性体の混合型有限要素解析に関する研究」と題し,6章よりなる. 現在,線形・非線形解析を問わず有限要素法により非圧縮性固体・流体や板・シェルの解析を精度良く行なうためには混合変分原理を用いることが不可欠であるとの認識が定着しつつある.非圧縮性固体を例にとれば,通常の変位型有限要素法は未知量として変位のみを用いるのに対し,混合型有限要素法では変位に加え,圧力なども独立な未知量として定式化を行なう点に特徴がある.しかしながら変位と圧力2つの場の有限要素近似を行なう補間関数の組み合わせが悪いと,場合によっては解の精度が著しく低下することが知られており,これは一般にロッキング現象とよばれている.ロッキングに関しては,現在までの研究で線形の範囲ではかなり完成された理論が存在しているが,これまでの要素開発は計算効率の向上を主眼とし,数学的な解析は敬遠されがちであった. 本研究の目的は,非圧縮性固体の極限的大変形解析に適した信頼性の高い要素開発を行なっていく上での指針を明確化することにある.これは混合要素自体は簡単に作ることができるが,その多くは信頼性が低くく,従って信頼性の高い要素の開発を行う必要があるが,その際に信頼性の高いものに共通する傾向があるならば,最初からそれをめざして要素を考えることにより,効率的に要素開発ができるからである. 第1章は緒言で,本研究の背景,目的及び関連分野における従来の研究を述べている. 第2章においては,線形弾性体に対する混合要素のロッキングについて考察を行っている.混合型要素がロッキングを起こさないための条件は混合型変分原理の安定性のための必要十分条件であるLBB条件と,その有限要素離散化を行なって得られる,離散化LBB条件によって与えられるが,ここでは非圧縮性線形弾性体を例に,一般的な抽象的パラメータ依存型問題に関する解の安定性の条件がLBB条件により与えられること,また混合型要素がロッキングを起こさないための為の条件が離散化LBB条件によって与えられることを示し,特にLBB条件の証明に関しては従来行なわれいるようなBanachのClosed Range Theoremを用いない方法で示している.次に離散化LBB条件を特異値解析によりある種の固有値問題に対応させ,数値的に予測する手法について示し,実際に2次元3角形,4角形要素,3次元4面体,6面体要素について,系統的に調査を行ない解析的な結果と比較することにより,この手法の妥当性を確認し,結果の整理を行っている.ここでとりあげた要素は現在よく用いられているものをほとんど含んでいるので,解析結果は広く実用に供するものと思われる. 第3章においては,ゴム材料のモデル化に適している超弾性体の混合型有限要素解析について考察している.まず代表的な超弾性体のポテンシャルとして知られているMooney-Rivlin体とそれを拡張した幾つかのポテンシャルを定義し,特に微圧縮性のポテンシャルについては厳密な議論に基づいてペナルティ係数と体積弾性係数が対応していることを示している.次に非/微圧縮性超弾性体の境界値問題を,有限要素法で解析を行なう際の弱形式化の方法としてLagrange未定乗数法,ペナルティ法及びそれらを包括する射影混合法を新たに導入し,三者の関係を明らかにしている. 第4章では,各種Mooney-Rivlin体有限要素の比較・検討を行い,LBB条件を満たさない要素はすべて解の信頼性は低くく,LBB条件を満たす要素についても不合理なものがあることを確認した.またLagrange未定乗数法と射影混合法には,数値計算の効率を含め,実質的な差はないが,ペナルティ法は同じ解析を行なうのに必要なstep数がけた違いに多く,計算効率の観点から大変形解析に向かないことを示している. 第5章では,極限的な変形の解析例として,捩じりを受けるロッドの"kinking"の解析を,良好な結果を収めた6面体要素を用いて行ない,kinkingの力学的特徴を明らかにした.また同問題において,LBB条件を満たさない他の幾つかの要素による解析結果との比較も行った. 第6章「結論」では,以上の成果を総括している. 以上を要するに,本研究は混合型有限要素法に共通する問題点である,ロッキング現象を起こさない要素の開発を行うために,線形問題の範囲では,厳密な数学的解析及びその数値解析手法について議論し,非線形問題に関しても,各種超弾性要素のよる比較・検討を行い,幾つかの重要な知見を得たものであって,工業上,また特に構造力学の観点から,工学上寄与するところが大きい.よって本論文は博士(工学)の学位請求論文として合格と認められる. |