| 内容要旨 | | 1.序 次世代における長距離通信の手段の,一つの有力な候補として「光ソリトン」の利用が挙げられている.従来の線形理論に基づく方法と比較すると,ソリトン通信では媒質の持つ非線形性と分散性とを積極的に利用していることがその特色である.この「光ソリトン」を理論的に解析する際のモデル方程式として用いられるのが,次の非線形シュレーディンガー方程式(Nonlinear Schr dinger Equation;以下ではNLS方程式と略す)と呼ばれる非線形偏微分方程式である; dinger Equation;以下ではNLS方程式と略す)と呼ばれる非線形偏微分方程式である;  (添字は微分を表す).ここで,右辺第1項は光ファイバーの持つ分散性を表し,第2項はKerr効果による非線形性を表す.ソリトンはこの2項のバランスによって形成されているのである. 光ソリトンの形成機構としては,今述べたような分散性と非線形性とのバランスによるものの他に,共鳴媒質の効果による「自己誘導透過(Self-Induced Transparency)」と呼ばれる現象が知られている.その現象は次のMaxwell-Bloch方程式(以下ではMB方程式と略記する)で記述される; 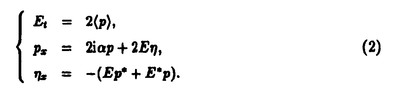 ここで,*は複素共役を表すものとする.また,〈p〉は共鳴周波数の不均一な広がりに関する平均化を表す; 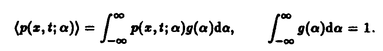 ファイバー中の光ソリトンの性質は基本的にはNLS方程式で理解されるのだが,近年の実験の進歩に伴い,方程式にさらに他の効果を採り入れると言う研究も進められている.MaimistovとManykinは,非線形共鳴媒質中の超短パルスを記述するためのモデル方程式として次の方程式を提出した;  この方程式はNLS方程式(1)とMB方程式(2)とを結合した形になっているので,以下ではNLS-MB系と呼ぶことにする. 数学的に見ると,これらの方程式はソリトン方程式の代表的な例になっていて,無限個の保存則の存在等の際立った特徴を持っている.物理現象のモデル方程式として重要なことは,これらの方程式に対する,いわゆる「ソリトン解」が具体的に構造されることである.(ここで「ソリトン解」とは,複数の孤立波が衝突の前後で,振幅などといった個性を失わずに伝播する解であることを意味している.この「個性を失わない」という著しい性質のために,長距離通信への利用が可能となるのである.) 本研究では,方程式の背後にある数学的構造を解析することを通して,これらの系における光ソリトンの伝播の様子を非摂動論的に調べることがその目的である.ソリトン方程式の持つ数学的構造に対して最も普遍的な視点を与える理論として,佐藤らによるKPヒエラルキーの理論がある.本研究ではこの理論に基づき,「NLS方程式+付加項」というタイプの方程式に対して,その解空間の構造を解析する.その際には,従来のKPヒエラルキーの理論に拡張を加えることが必要となる.今回考察したのは次の2点である; ・「多極的な」時間発展の導入 ・方程式の複素構造の代数的特徴付け 以下では,節を改めて,この2点の内容を述べていく. 2.「多極的な」時間発展の導入 KPヒエラルキーにおいては,その時間発展は(ある意味で)線形化される.そこでの時間発展は,本質的には  という形をしているものと考えられる.この関数はk=∞に特異性を持っていることを注意しておく.一方,上野・高崎両氏によって定式化された戸田格子ヒエラルキーにおける時間発展は, 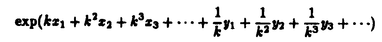 であり,特異点はk=0とk=∞の二箇所である. 本研究では,戸田格子ヒエラルキーをさらに拡張し,さらに多くの特異点を持つような時間発展,すなわち,  というタイプの時間発展をも取り扱い得る枠組を提出した.(MB方程式はこのクラスに属する.)その方法に基づけば,MB方程式(2)に対して,ソリトン解等の具体的な解が,初等的な代数計算のみによって構成される.より具体的に述べると,ロンスキー型の行列式(正確には"double-Wronskian)を用いて特解が構成されるのである. このようにMB方程式をヒエラルキーの一員としてとらえることの利点の一つとして,ヒエラルキーに含まれる他の方程式との結合系が容易に捉えられることが挙げられる.例えばNLS-MB系(3)を考えてみよう.この方程式に関しても,今回導入した手法を用いてソリトン解を構成することが可能である.解の代数的構造としてはMB方程式と大差ないが,実際にソリトン解を構成してみると,その分散関係の違いから振舞いが多少異なってくる.特に,多ソリトンの"束縛状態"を考えると,NLS方程式,MB方程式各々一方のみでは起こらない「非対称的に振動するソリトン」が見られる(Figure 1).  Figure 1:2ソリトンの束縛状態の例;(a)NLS方程式(対称的),(b)NLS-MB系(非対称的).3.ソリトン方程式の複素構造の代数的特徴付け Figure 1:2ソリトンの束縛状態の例;(a)NLS方程式(対称的),(b)NLS-MB系(非対称的).3.ソリトン方程式の複素構造の代数的特徴付け NLS方程式(1)は,物理系のモデル方程式としては電場の複素振幅を記述するものである.そのため,(1)において,E=E(x,t)は複素数に値をとる関数となる.このことは,方程式の解空間に何らかの複素構造が付加されることを意味するが,これまでのところKPヒエラルキーに対して,その複素構造を取り扱った研究はなされていない. KPヒエラルキーの解を,より代数的に記述する方法として,伊達らによるフェルミオン演算子を使う方法がある.この方法によると,KPヒエラルキーの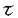 -関数は, -関数は,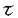 =〈eH(x)g〉という形に表すことができる.ここで,gはクリフォード群の元であり,ソリトン解等の様々な特殊解は,このgの形を特定することで得られる. =〈eH(x)g〉という形に表すことができる.ここで,gはクリフォード群の元であり,ソリトン解等の様々な特殊解は,このgの形を特定することで得られる. 本研究では,フェルミオンの空間の自己同型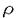 を適当に定義し,上のgに を適当に定義し,上のgに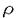 (g)=g*(*は複素共役)という制限をつけることで,ソリトン方程式の複素構造を取り扱い得ることを示した.また,「NLS方程式+付加項」というタイプの方程式のうち「微分型」と呼ばれる方程式に対しても同様の解析を行ない,そこに現れる複素構造が通常のNLS方程式のそれとはことなることを見い出した.この結果は,複素構造の分類により,可積分なNLS型方程式の分類が可能となることを示唆している. (g)=g*(*は複素共役)という制限をつけることで,ソリトン方程式の複素構造を取り扱い得ることを示した.また,「NLS方程式+付加項」というタイプの方程式のうち「微分型」と呼ばれる方程式に対しても同様の解析を行ない,そこに現れる複素構造が通常のNLS方程式のそれとはことなることを見い出した.この結果は,複素構造の分類により,可積分なNLS型方程式の分類が可能となることを示唆している. 4.まとめと今後の展望 本研究では,KPヒエラルキーの手法を拡張することにより,光ソリトンのモデル方程式として現れる「NLS方程式+付加項」というタイプの方程式を解析した.その結果,「非対称的に振動する束縛状態」という,これまでに知られていなかったパルスの振舞いが得られた. また,NLS型方程式の複素構造が自由フェルミオンの自己同型という代数的な言葉で定式化できることを示し,通常のNLS方程式と微分型NLS方程式との複素構造の違いを明らかにした. ここで開発した手法を,他の物理系のモデル方程式に適用し,その解を調べていくとともに,さらに新たなソリトン方程式を探索していくことを今後の課題としたい. |
| 審査要旨 | | 本論文は「Solutions for Equations of Nonlinear Schr dinger-Type(非線形シュレーディンガー型方程式の解)」と題し、光ソリトンのモデル方程式であるところの、ある種の非線形偏微分方程式の解を具体的に与えるとともに、解空間の代数的構造を解析したものである。 dinger-Type(非線形シュレーディンガー型方程式の解)」と題し、光ソリトンのモデル方程式であるところの、ある種の非線形偏微分方程式の解を具体的に与えるとともに、解空間の代数的構造を解析したものである。 近年、次世代における長距離通信の有力な手段として、ファイバー中の光ソリトンの利用が提唱され、注目を浴びている。光ソリトンは、伝播に際して著しい安定性を持つため、長距離通信への応用が期待され、実際の通信システムに利用することを目指し、これまでにも高次項の与える影響などが、実験・理論の両面から研究されてきた。理論的な観点からいうと、ファイバー中の光ソリトンの挙動は、基本的には非線形シュレーディンガー方程式と呼ばれる非線形偏微分方程式で記述される。その方程式はソリトン系としての美しい代数的構造を持っているため、非線形であるにも関わらず厳密に取り扱うことが可能であることが知られている。しかし、方程式の解空間の代数的構造という点では、これまで非線形シュレーディンガー方程式単独の解が主に考察され、他の相互作用の影響は摂動論的にしか取り扱われていなかった。また、非線形シュレーディンガー型方程式特有の構造である複素構造には、ほとんど注意が払われていなかった。 本論文の目的は、このような状況を踏まえて、非線形シュレーディンガー方程式に対する他の効果の影響を非摂動論的に取り扱い、工学的に重要な解を具体的に与えるとともに、その解空間の代数的構造を統一的な視点から捉えることにより、光ソリトンの振舞いを解析していくことである。 論文は5章より成っている。 第1章は「Introduction」であり、本研究の背景と目的、及び本論文の構成について述べている。 第2章は「2-Component Version of Toda Lattice Hierarchy」と題し、本論文での理論展開の基礎となる戸田格子ヒエラルキーの理論をまとめ、その立場から非線形シュレーディンガー方程式の解の構成法を述べている。戸田格子ヒエラルキーの立場から非線形シュレーディンガー方程式を取り扱うには、解空間に制限をおきリダクションを行う必要があるが、そのリダクションの条件、及び従来は余り注意が払われていなかった複素共役の条件が、本研究においては、代数方程式に対する付加条件として簡明に捉えられている。従来の双線形化法の立場からは、ソリトン解等といった個々の具体例に対してさえも、複素共役の条件に関しては煩雑な計算による証明が必要であり、一般論のレベルにまでは達していなかった。 第3章は「Multi-Pole Extension of Toda Lattice Hierarchy」と題し、戸田格子ヒエラルキーという微分方程式系に対し、従来は取り扱われていなかった時間発展方向を付加し、その下での厳密解の構成法を与えている。また、新たに付加した時間発展を利用して取扱い得る方程式の例として、まず電磁場と2準位原子との共鳴相互作用を記述するマックスウェル・ブロッホ方程式の解の構成法を述べている。次に、ファイバー中の光ソリトンと2準位原子との相互作用を記述するモデル方程式としてMaimistovとManykinによって提出された、非線形シュレーディンガー方程式とマックスウェル・ブロッホ方程式との結合系を考察し、その解の構成法を与えるとともに、「非対称的に振動するソリトン」という、通常の非線形シュレーディンガー方程式においては見られなかった現象を発見している。さらに、場の理論のモデル方程式であるカイラル場の方程式に対しても、本論文で導入した手法が有効であることを示している。 第4章は「Complex Structures in NLS-Type Equaitons」と題し、通常の非線形シュレーディンガー方程式、微分型非線形シュレーディンガー方程式という2つの方程式に対して、それらの複素構造の持つ代数的意味を、リー代数的な視点から考察している。非線形シュレーディンガー方程式に限らず、ソリトン方程式の解空間には、アフィン・リー代数が無限小変換として作用することが伊達らの研究によって明らかにされているが、そこでは複素構造については考察されていなかった。本研究においては、アフィン・リー代数の同型写像として複素構造を捉え、2つの非線形シュレーディンガー型方程式の複素構造が本質的に異なることを見いだしている。積分可能な高次非線形シュレーディンガー方程式の探索は、これまでは個別になされてきたが、本研究では、それらに対する統一的な視点からの分類の可能性を示唆するとともに、ソリトン方程式の複素構造とアフィン・リー代数の実形との対応という、数学的にも新しい視点を提供している。 第5章では、本論文で得られた結果を簡潔にまとめるとともに今後の展望を述べ、「Summary and Concluding Remarks」としている。 以上を要約すると、本研究では、光ソリトンを記述するモデル方程式である非線形シュレーディンガー型の方程式に関し、解を具体的に与えるとともに、その解空間の代数的構造を新たな視点から解析している。特に、非線形シュレーディンガー方程式で記述される光ソリトンに対しての、2準位原子との共鳴相互作用の効果の考察から、「非対称的に振動するソリトン」という、これまでに知られていなかった振舞いを発見している。また、方程式の持つ複素構造に注目し、通常の非線形シュレーディンガー方程式と、微分型非線形シュレーディンガー方程式とでは複素構造が本質的に異なることを明らかにするととともに、その立場からの高次非線形シュレーディンガー方程式の分類を提案している。本研究から得られた非線形シュレーディンガー型方程式の解空間に関する知見は、光ソリトンに対する高次効果の影響の理解に供すること大であり、物理工学の基礎、特に非線形波動論への貢献が大きい。よって、本論文は、博士(工学)の学位請求論文として合格と認められる。 |