| 内容要旨 | | 観測されたデータからこのデータのしたがう未知の確率分布を推定する問題を考察する場合,一般的には有限次元のパラメータのみで確率分布が完全に決まるパラメトリックモデル{p( , , )}を仮定して,パラメータ )}を仮定して,パラメータ に関する様々な推定法について議論する.数多くの推定法の中でも漸近的に有効な最尤推定法は推定理論の中心的な位置を占めている.しかし,実際にはデータのしたがう確率分布に関して十分な知識がないことも多く,パラメトリックモデルにおいて仮定した分布形が妥当かという問題が生じる.また,Neyman and Scott[1948]により観測とともに撹乱パラメータが増加するモデル(Neyman-Scott問題)においては最尤推定量が一致性を持たない例が存在することが示され,従来のパラメトリックモデルの枠を越えた無限次元の統計モデルを考える必要性が認識されるようになった.このような経緯から,有限個の興味あるパラメータ に関する様々な推定法について議論する.数多くの推定法の中でも漸近的に有効な最尤推定法は推定理論の中心的な位置を占めている.しかし,実際にはデータのしたがう確率分布に関して十分な知識がないことも多く,パラメトリックモデルにおいて仮定した分布形が妥当かという問題が生じる.また,Neyman and Scott[1948]により観測とともに撹乱パラメータが増加するモデル(Neyman-Scott問題)においては最尤推定量が一致性を持たない例が存在することが示され,従来のパラメトリックモデルの枠を越えた無限次元の統計モデルを考える必要性が認識されるようになった.このような経緯から,有限個の興味あるパラメータ 以外に,分布の形状を表す無限次元(関数自由度)の撹乱パラメータ 以外に,分布の形状を表す無限次元(関数自由度)の撹乱パラメータ を含むセミパラメトリックモデル{p( を含むセミパラメトリックモデル{p( , , , , )}が導入され.この無限次元の統計モデルに基づいて興味あるパラメータ )}が導入され.この無限次元の統計モデルに基づいて興味あるパラメータ の推定問題が近年盛んに研究されている. の推定問題が近年盛んに研究されている. セミパラメトリックモデルに基づく推定理論は情報量限界に関する研究,局所的ロバスト推定量に関する研究,広域的ロバスト推定量に関する研究と大きく3つに分けられる.本研究は広域的ロバスト推定量,すなわち,セミパラメトリックモデルに属するあらゆる分布に対して一致性を持つ推定量を求めることを目的としている.広域的ロバスト性を持つ推定量を議論するための有用な道具としてGodambe[1960,1976]によって導入された推定関数という概念がある. セミパラメトリックモデル{p( , , , , )}を考える,撹乱パラメータ )}を考える,撹乱パラメータ によらない によらない と と (簡単のためスカラーパラメータとする)の関数で,任意の (簡単のためスカラーパラメータとする)の関数で,任意の に対して期待値が0になるものを推定関数という. に対して期待値が0になるものを推定関数という.  ただし, は分布p( は分布p( , , , , )に関する期待値を表す.もし,このような関数が存在すれば.i.i.d.観測データ )に関する期待値を表す.もし,このような関数が存在すれば.i.i.d.観測データ 1,… 1,… nが得られたときに方程式 nが得られたときに方程式  の解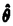 は広域的ロバスト推定量となる.すなわち,真の撹乱パラメータ は広域的ロバスト推定量となる.すなわち,真の撹乱パラメータ 0がどのようなものであっても推定量 0がどのようなものであっても推定量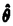 は は 一致推定量である. 一致推定量である. このように,推定関数が存在すれば広域的ロバスト推定量が構成できるが,与えられたセミパラメトリックモデルに対して推定関数を具体的に求めることは容易ではない.これまでは推定関数の存在条件や最適な推定関数の特定というような基本的な問題についてほとんどわかっていなかった.Amari and Kumon[1988]は観測とともに撹乱パラメータが増えるモデル(Neyman-scott問題)において情報幾何学(Amari[1985])の方法を用いて推定関数が解析できることを示し.推定関数に関する諸問題に解答を与えた.さらに,Amari and Kawanabe[1994]はこれを一般のセミパラメトリックモデルに拡張して推定関数に関する以下のような諸問題に明確な解答を与えた. 1.どのような場合に推定関数は存在するのか? 2.推定関数全体の集合はどういうものか? 3.最適な推定関数は何か? 4.どのような場合に最適な推定関数は有効であるか? 推定関数を用いた場合の情報量損失はどれぐらいか? 5.どのようにして最適あるいはそれに近い推定関数を構成するか? Amari and Kumon[1988]ではNeyman-Scott問題のように最適な推定関数が撹乱パラメータに依存しない場合を興味の対象であったが,Amari and Kawanabe[1994]で扱う一般のセミパラメトリックモデルにおいては最適な推定関数は撹乱パラメータ に依存するため,最適な推定関数uI( に依存するため,最適な推定関数uI( , , , , 0)( 0)( 0は真の撹乱パラメータ)をどのように推定・近似するかということが重要な課題になる.この点に関しては基本的にはBickel[1982,1993]の適応的推定法と同様に観測データより撹乱パラメータの推定量 0は真の撹乱パラメータ)をどのように推定・近似するかということが重要な課題になる.この点に関しては基本的にはBickel[1982,1993]の適応的推定法と同様に観測データより撹乱パラメータの推定量 を構成し,そこでの最適推定関数uI( を構成し,そこでの最適推定関数uI( , , , , )を用いる.ところで,最尤推定法を元にしたBickelの適応的推定法は推定量 )を用いる.ところで,最尤推定法を元にしたBickelの適応的推定法は推定量 が真値 が真値 0に収束すれば興味あるパラメータの推定量 0に収束すれば興味あるパラメータの推定量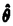 は一致性を持ち,情報量の意味で有効であるが.そうでない場合には推定量 は一致性を持ち,情報量の意味で有効であるが.そうでない場合には推定量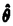 は一致性を持たなくなる.これに対して,最適推定関数uI( は一致性を持たなくなる.これに対して,最適推定関数uI( , , , , )に基づく適応的推定法は一般には情報量の意味で効率が落ちるが,推定量 )に基づく適応的推定法は一般には情報量の意味で効率が落ちるが,推定量 としてたとえ全く違ったものをとっても としてたとえ全く違ったものをとっても 一致性が保証される.すなわち,推定関数の利点を生かせば, 一致性が保証される.すなわち,推定関数の利点を生かせば, として粗い推定量を用いて実用的なセミパラメトリック推定量が構成できる. として粗い推定量を用いて実用的なセミパラメトリック推定量が構成できる. 本論文の目的は,第1にAmari and Kawanabe[1994]の推定関数の幾何学理論を整理し,この理論の本質と数学的な問題点を説明することである(第2章).第2に統計学や工学で実際に使われる具体的な統計モデルに幾何学理論を応用してこの理論の有用性を示すことである.ここでは2次元直線当てはめ問題(第3章)と楕円分布モデル(第4章)を取り上げ.その推定関数とセミパラメトリック推定法について議論した. 2次元直線当てはめ問題とは直線y=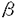  + +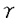 上にのっている真値に,独立な正規誤差 上にのっている真値に,独立な正規誤差 が加わった2次元データ が加わった2次元データ  がn個独立に観測されたとき,この直線(傾き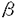 と切片 と切片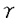 )を推定する問題である.この問題では真値の位置 )を推定する問題である.この問題では真値の位置 が観測とともに増加する撹乱パラメータとなり,Neyman-Scott問題の1種であるので理論上重要な統計モデルである.また,図像解析の諸問題はこれを一般化した線形(非線形)当てはめ問題として定式化できることが知られており,応用上も重要なモデルである.真値の系列 が観測とともに増加する撹乱パラメータとなり,Neyman-Scott問題の1種であるので理論上重要な統計モデルである.また,図像解析の諸問題はこれを一般化した線形(非線形)当てはめ問題として定式化できることが知られており,応用上も重要なモデルである.真値の系列 の扱い方には非確率的な数列とみる立場と未知の分布k( の扱い方には非確率的な数列とみる立場と未知の分布k( )からのi.i.d.確率変数列とみる立場があるが.ここでは後者の場合(ミクスチャーモデル)を扱う.幾何学理論を用いて推定関数の集合を特定することができて,最適な推定関数が条件付スコア関数であることがわかる.さらにこの結果,最尤推定法(この場合最小自乗法に一致)が推定関数法になっており,最尤推定量は真値の分布k( )からのi.i.d.確率変数列とみる立場があるが.ここでは後者の場合(ミクスチャーモデル)を扱う.幾何学理論を用いて推定関数の集合を特定することができて,最適な推定関数が条件付スコア関数であることがわかる.さらにこの結果,最尤推定法(この場合最小自乗法に一致)が推定関数法になっており,最尤推定量は真値の分布k( )によらずに )によらずに 一致性を持つことが示される.しかし,最尤推定法は一般には推定関数法の中で有効な方法ではなく,特に原点を通る直線( 一致性を持つことが示される.しかし,最尤推定法は一般には推定関数法の中で有効な方法ではなく,特に原点を通る直線(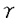 =0)を当てはめる場合には真値 =0)を当てはめる場合には真値 の平均と分散の情報(推定量)を用いることによって最尤推定法を改良する推定関数法(L*-推定関数法)を構成することができる.L*-推定関数法は真値の分布 の平均と分散の情報(推定量)を用いることによって最尤推定法を改良する推定関数法(L*-推定関数法)を構成することができる.L*-推定関数法は真値の分布 ( ( )が正規分布の場合の最適推定関数法であり,また推定量の漸近分散をリスク関数としたときのミニマックス推定法でもある. )が正規分布の場合の最適推定関数法であり,また推定量の漸近分散をリスク関数としたときのミニマックス推定法でもある. 楕円分布とはd次元確率変数 の密度関数の水準面がRd内の楕円体になっているような確率分布,すなわち, の密度関数の水準面がRd内の楕円体になっているような確率分布,すなわち,  と表されるような確率分布のことである,このような確率分布からなる統計モデル{p( , , , , )}を楕円分布モデルという.ここで,推定したいパラメータ )}を楕円分布モデルという.ここで,推定したいパラメータ は分布の中心 は分布の中心 ∈Rdおよび,疑似分散行列V(d×d正定値対称行列)である.また, ∈Rdおよび,疑似分散行列V(d×d正定値対称行列)である.また, (・)は[0,∞)上の未知の非負値関数であり,関数自由度を持つ撹乱パラメータとする.楕円分布モデルは多変量解析において正規分布モデルの1つの拡張であり,近年多変量正規分布に基づく推測手法を楕円分布モデルに拡張する研究が盛んに行なわれている.パラメータの識別可能性の問題から,これまでの研究ではVの形状を表すパラメータV/trVだけに関するセミパラメトリック推定問題が扱われていて.関数 (・)は[0,∞)上の未知の非負値関数であり,関数自由度を持つ撹乱パラメータとする.楕円分布モデルは多変量解析において正規分布モデルの1つの拡張であり,近年多変量正規分布に基づく推測手法を楕円分布モデルに拡張する研究が盛んに行なわれている.パラメータの識別可能性の問題から,これまでの研究ではVの形状を表すパラメータV/trVだけに関するセミパラメトリック推定問題が扱われていて.関数 (・)の一致推定量を用いれば (・)の一致推定量を用いれば (・)が既知であるときのFisher情報量を達成する推定量が構成できることと,真の (・)が既知であるときのFisher情報量を達成する推定量が構成できることと,真の 0(・)を含まない非忠実な有限次元関数族{ 0(・)を含まない非忠実な有限次元関数族{ (・, (・, )}を仮定したときの(疑似)最尤推定量が )}を仮定したときの(疑似)最尤推定量が 一致推定量になることが知られている.これに対して本論文では 一致推定量になることが知られている.これに対して本論文では の分散の存在を仮定して分散行列V全体の推定を行なう.この場合,疑似最尤推定量はVの大きさtrVに関しては一般的に一致性がない.しかし,推定関数の集合および最適な推定関数を計算した結果,疑似最尤推定法の尤度方程式を修正した推定方程式を用いた推定関数法により の分散の存在を仮定して分散行列V全体の推定を行なう.この場合,疑似最尤推定量はVの大きさtrVに関しては一般的に一致性がない.しかし,推定関数の集合および最適な推定関数を計算した結果,疑似最尤推定法の尤度方程式を修正した推定方程式を用いた推定関数法により ,Vの ,Vの 一致推定量を作れることが示された. 一致推定量を作れることが示された. 推定関数の幾何学理論は,理論面では数学的な問題点を解決してさらに厳密化が必要であり.応用面でも最適な推定関数を近似する推定関数としてどのようなものを用いるのがよいかという問題に関しては個々のモデルに関してさらに工夫が必要である.しかし,本論文で示したように幾何学理論は様々なセミパラメトリックモデルの推定関数を統一的に解析できる有用な方法である. |