情報量規準AIC最小化法などの「モデル選択」は非常に有用である.しかし,モデル間のAICの差が,その標準誤差に対して十分に大きくなければ,AICを最小にするモデルが最も良いとは言えない.AICの第1項に相当する最大対数尤度は,比較的大きな分散を持つので,これを考慮してモデル選択の信頼性を評価する必要がある.そこで,一つだけモデルを選ぶのではなく,複数のモデルを選ぶことにする.選んだモデルの集合は,最も良いモデルを含み,なるべく小さい方がよい.その集合を「モデル信頼集合」とよび,多重比較の立場から誤り確率を押える.AIC最小化法を「点推定」にたとえれば,モデル信頼集合は「区間推定」に相当する.

　モデル選択の信頼性を評価しようとする研究は以前からある.Cox検定は分離可能な二つのモデルの比較をする.Spjtvollらの方法は重回帰モデルの変数選択のための多重比較法である.Felsensteinらの方法はAIC最小モデルの選択確率をbootstrapにより推定する.これらは,扱う対象が限定されていたり,信頼集合の意味が曖昧である点が問題である.一方,本論文で提案する方法は,一般の確率モデルを対象とし,信頼集合の意味も多重比較によって明確に与えられる点において優れている.ただし,これらの手法の性質の違いや相互の関係は十分に議論されておらず,これからの課題である.

　本論文ではAICを用いたが,モデル選択のための規準はAICの他にも提案されている.それらの多くは,第1項が最大対数尤度に相当し,AICと同様に分散が大きいという問題を持つ.これらの規準にも,本論文の議論は,そのまま適用することが可能である.一方,AICはモデル選択の「一致性」を持たないなどの問題が指摘されている.しかし一致性の問題は,特殊な状況での議論であり,一致性がないからといって実用上不利だとはいえない.また,一致性を持つといわれるMDLなどの規準でも,モデルの関係が入れ子でないある状況下では,一致性を持たなくなることを本論文では示している.その状況でも,情報量規準の第2項を工夫することによって,常に一致性をもつ規準をつくることはできるが,規準の意味は曖昧になる.AICは予測の観点から導かれる自然な規準であり,その意味が明確である.このような点を考慮して,本論文ではAICを採用した.ただし数理的な議論では,より精密なTICを用いている.

　AIC最小化法では各モデル毎にAICの値を計算し,モデルをAICの小さい順に並べて,AICを最も小さくするモデルだけを選ぶ.一方,本論文の方法では,候補となるモデルの集合とデータが与えられたとき,各モデル毎に「P-値」を計算する.そして,P-値の大きい順にモデルを並べて,有意水準以上のP-値のモデルを,モデル信頼集合の要素とする.

　モデルのP-値は多重比較の方法で計算する.本論文ではTukey法,Holm法,Gupta法を用いた.Tukey法とGupta法では,「誤り」の定義が異なる.Tukey法では,良いモデルのうち一つでも信頼集合からもれてしまうことを誤りとし,その確率を有意水準で押える.Gupta法では,良いモデル各々について,それが信頼集合からもれてしまう確率を有意水準で押える.このような違いを踏まえ,仮説検証的にモデル選択をする場合はTukey法,モデル探索の場面ではGupta法などと,目的に応じて使い分ける.Holm法は,Tukey法と同じ誤り確率を押えながらも,信頼集合が小さくなる傾向があり,Tukey法より優れている.

　本論文のP-値の計算では,いくつかの近似をする.すなわち,AICの差は漸近的に正規分布に従い,その分散の推定量を真値とみなしてしまう.その結果,得られるP-値は近似値であり,名目上のP-値である.AICの差の分散の推定量は,AICの導出と同様に,漸近展開の第2項まで考慮して求めた.これは,比較する二つのモデルが共に真の分布を含むような場合を,考慮することに相当する.

　本論文で提案するモデル信頼集合は「保守的」である.すなわち,誤り確率が有意水準よりも小さくなる傾向がある.これは,結果として信頼集合が大きくなってしまう傾向を意味する.誤り確率が有意水準より大きいと,信頼集合の意味が曖昧になるので,それに比べれば保守的である方が良い.しかし本来ならば,誤り確率はなるべく有意水準に等しい方が良い.保守的であることの原因の一つは,P-値の計算における近似,もう一つは多重比較法そのものの性質である.誤り確率を有意水準に近付けて,信頼集合をより小さくすることは,これからの課題である.

　誤り確率の評価では,データ数が十分に大きいとする漸近理論を用いた.本論文では一般的な確率モデルを対象とするので,なんらかの漸近理論に頼らざるを得ない.特に,比較する二つのモデルの「最適分布」が異なる場合及び一致する場合に分けて議論した.ここで,最適分布とは,真の分布を各モデルに射影した点である.さらに,計算上の技法として,各モデルをO(1/)のオーダで真の分布に近付ける場合を考えた.これらの場合分けにより,データとモデルの相対的な関係の様々な局面において,信頼集合の性質を評価したことになる.ただし,データ数が小さい場合には,漸近理論による近似計算の誤差は無視できないので,注意が必要である.

　モデル探索の初期段階では,データ数に対してモデルの候補数が多く,信頼集合として多くのモデルが選ばれることがある.そのとき,選ばれたモデルの構造に共通する性質を見つけ出すことは,応用上重要である.これに対する一つのアプローチとして,本論文では「モデルの地図」を提案する.これにより,各モデルの良さや互いの関係を幾何学的に捉えられる.AIC最小化法のようにモデルを一つだけ選ぶ手法と比較して,モデルの信頼集合と地図によるモデル探索は,あり得る可能性を積極的に拾い上げることに重点をおいた手法と言える.

　モデル地図を描くために,各モデル間の「距離」を定義する.本論文では,AICの差の標準誤差,もしくはその推定量をもってモデル間距離とする.真の分布が各モデルに十分近いとき,漸近的にモデル間距離は,K-L情報量で計った最適分布間距離に相当する.従って,モデル地図で見ているのは,各モデルの最適分布の,確率分布の空間における相対的な位置関係である.一方,AICでモデルの「高さ」を定義する.二つのモデルの高さの差をモデル間距離で割った「傾き」は,相対的なモデルの良さを表す.多重比較法では,候補となるすべてのモデル間の傾きを,同時に考慮して信頼集合を構成している. 重回帰モデルにおける変数選択問題は,モデル選択の一例である.いくつかの実データと合成データについて,モデル信頼集合やモデル地図を計算し,本論文で提案する方法の有効性を示した.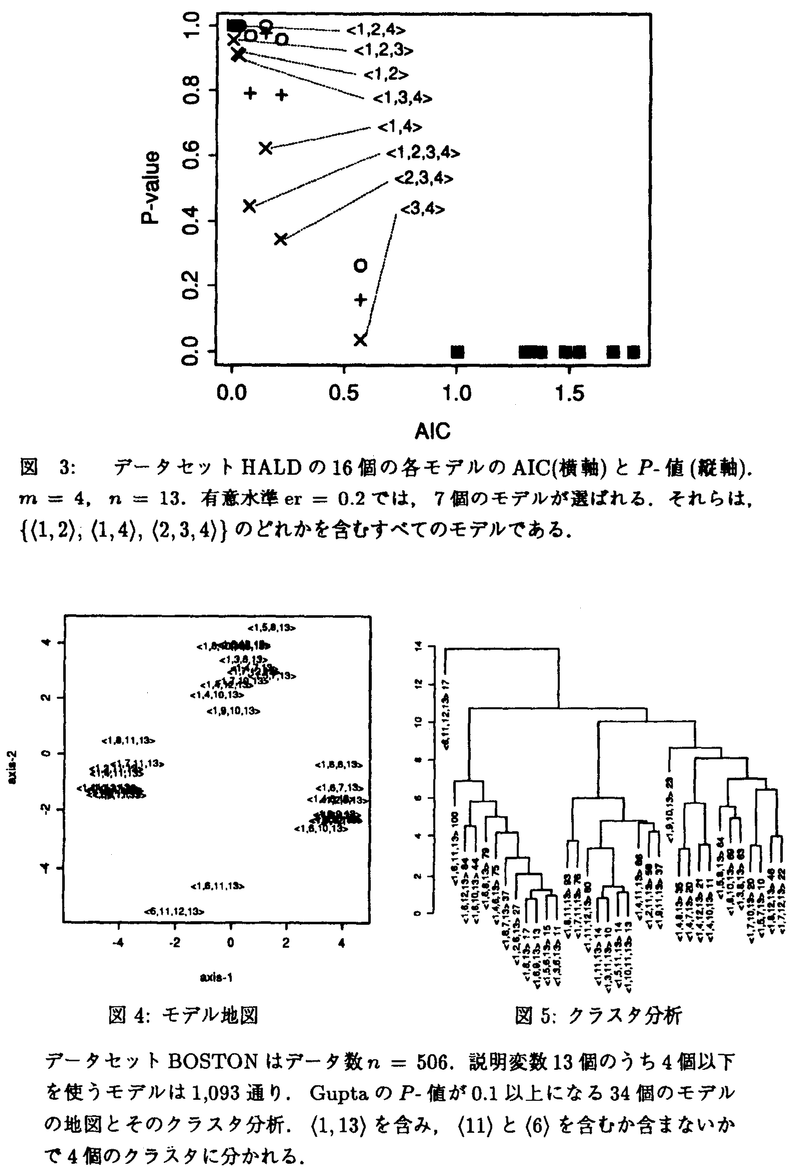

図表図1:データセットBABYの16個の各モデルのAIC(横軸)とP-値(縦軸).説明変数はm＝4個,データ数はn＝15である.TukeyをO,Holmを+,GuptaをXで表す.どの方法でも,有意水準er＝0.2では,〈1〉を含む8個のモデルが選ばれる.AIC最小モデルをAIC＝0としてある.各モデルのラベルは説明変数の番号を〈・〉で囲って示した. / 図2:データセットBABYのモデル〈1〉を含む8個のモデルの地図を,Torg-ersonの多次元尺度構成法を用いて,3次元空間で表現したもの.

図表図3:データセットHALDの16個の各モデルのAIC(横軸)とP-値(縦軸).m＝4,n＝13.有意水準er＝0.2では,7個のモデルが選ばれる.それらは,{〈1,2〉,〈1,4〉,〈2,3,4〉}のどれかを含むすべてのモデルである. / 図4:モデル地図 / 図5:クラスタ分析 データセットBOSTONはデータ数n＝506.説明変数13個のうち4個以下を使うモデルは1,093通り.GuptaのP-値が0.1以上になる34個のモデルの地図とそのクラスタ分析.〈1,13〉を含み,〈11〉と〈6〉を含むか含まないかで4個のクラスタに分かれる.

　本論文は,「統計的モデル選択の研究-モデルの信頼集合の構成-」と題し,6つの章と付録からなる.

　対象の振舞いを未知母数を含む確率モデルで表現し,観測したデータから母数を推定する方法は広く応用されている.推定した母数は,予測などの推測やそれに基づく制御などに用いられる.ところが,対象を表現する確率モデルが先験知識から一意に決まらず,いくつかの候補の中からデータに基づいて選択する必要がしばしばある.これは統計的モデル選択の問題と呼ばれる.特に,AIC(Akaike Information Criterion-赤池情報量規準)は,平均予測誤差の推定量として提案され,これを最小にするモデルを選ぶ方法は,簡便で有用な方法として一般に用いられている.しかし,モデル間のAICの差が,その標準誤差に対して十分に大きくなければ,AICを最小にするモデルが最も良い予測をするとは言えない.AICの第1項に相当する最大対数尤度は.比較的大きな分散を持つので,これを考慮してモデル選択の信頼性を評価する必要がある.

　本論文の目的は,一つだけモデルを選ぶのではなく,複数のモデルを選ぶことによって,選択の信頼性を定量的に与える方法を提案することにある.選んだモデルの集合は,最も良いモデルを含み.なるべく小さい方がよい.その集合を「モデル信頼集合」とよび,すべての対比較を同時に検定する,いわゆる多重比較の立場から誤り確率を押える.信頼集合に含まれるモデルの間では,その良さに有意な差はない.AIC最小化法を「点推定」に例えれば,モデル信頼集合は「区間推定」に相当する.

　第1章は序論である.ここでは,まずモデル選択の必要性を応用例を通して示し,第2章から第6章及び付録での議論を,総括して述べている.

　第2章は,情報量規準AICについて述べている.ここでは.第3章以降で必要になる数学的な準備をした上で,AICの数理的な性質をまとめている.

　第3章は,AICの差の統計的性質について述べている.ここでは比較するモデルの関係を3通りに分類し、それぞれについて,AICの差の漸近分布を示し,期待値や分散を与えている.この結果を,第4章以下で用いる.

　第4章は,モデル選択の一致性について述べている.候補の中で一番良いモデルを選択する確率が,漸近的に1に収束することを,モデル選択の一致性と呼ぶ.特殊な状況を考えると,AIC最小化法によるモデル選択は一致性を持たないことがあるが,MDL(Minimum Description Length)など他のモデル選択規準でも,同様に一致性を持たない場合があることを本章では示している.一般的な状況を考えれば,AICでもMDLでも一致性を持つこと,及び,一致性はデータ数が無限大の極限の議論であって,現実にはデータ数は有限であることなどを考慮すれば,そもそも以前の研究でしばしば行なわれているような,一致性によるモデル選択規準の善し悪しの議論自体にあまり意味がない.むしろ,有限のデータ数ではいかなるモデル選択規準でも誤りを犯す可能性があるので,その信頼性の評価をすべきであると主張している.

　第5章は,多重比較について述べている.モデルの信頼集合は,一番良いモデルを含む確率を一定の水準に保ちながら,なるべく小さな集合としたい.このために,多重比較の方法をモデル選択に応用する.一般に用いられている多重比較法は,変量間の相関構造が既知の場合を扱っているのに対し,モデル選択に応用するには,その相関構造も推定する必要がある.従って,TukeyやGuptaなどの多重比較の方法を,本論文では一般化して用いている.

　第6章は,これまでの章での結果を踏まえて,モデル信頼集合の構成法を示し,さらにその誤り確率の評価について述べている.多重比較の方法をモデル選択に応用する時にいくつかの近似計算を行なう.従って,モデル信頼集合の誤り確率,すなわち一番良いモデルを含まない確率が,近似計算によってどのような影響を受けるかを調べる必要がある.ここでは漸近的な議論によって,誤り確率があらかじめ設定した有意水準より小さくなる傾向があることを示している.

　付録はA,B,Cの3つから成る.(A)ではモデル探索を視覚的に行なうためのひとつの試みとして,モデル地図について述べている.(B)では,変数選択問題への応用に必要な統計量を与え.いくつかの現実のデータへの適用例を通して本論文の方法の有効性を示している.(C)は記号の説明である.

　以上要するに本論文は,従来はあまり注意の払われていなかったモデル選択の信頼性を,多重比較の立場からモデル信頼集合を構成することによって定量的に評価する方法を提案したものであり,数理統計,及びそれを用いるパターン認識や制御理論など工学の様々な分野に貢献するところが大きい.よって本論文は博士(工学)の学位請求論文として合格と認められる.