球面からリー群への調和写像は、物理学の方面からの刺激もあり、近年活発に研究されるようになった。それらの多くは、ツイスター理論や可積分系の理論を用いて、調和写像の構成を行うというものである。 Uhlenbeckは、そのなかでも先駆的な研究を行った。つまり、2次元球面からユニタリ群への調和写像に対しある線形微分方程式系を対応させ、その方程式系の解がツイスターリフトとなるようなツイスター理論を作った。またそれにより調和写像の構成やその空間の代数的考察を行った。このとき調和写像の空間にある階級付け(uniton number)が生まれることがわかるのであるが、この論文ではこの階級付けがどのような微分幾何学的意味をもつのかを考察した。 まず調和写像の説明を行う。(M,g),(N,h)をリーマン多様体とする。滑らかな写像 :M→Nがharmonicとは、 :M→Nがharmonicとは、 がエネルギー汎関数 がエネルギー汎関数 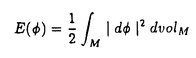 の臨界点であることである。  をリーマン面、U(n)をユニタリ群 をリーマン面、U(n)をユニタリ群  とする。また、ループ群 U(n)と写像 U(n)と写像 : : U(n)→U(n)を、次で定義する。 U(n)→U(n)を、次で定義する。   U(n)は無限次元リー群でKahler多様体であることがわかっている。任意に調和写像 U(n)は無限次元リー群でKahler多様体であることがわかっている。任意に調和写像 : : →U(n)をひとつ固定し、次の線形微分方程式系 →U(n)をひとつ固定し、次の線形微分方程式系  を考える。 定義(Uhlenbeckによる。1989年)  に対し、(1)の解 に対し、(1)の解 が存在するとき、 が存在するとき、 を を のextended solutionという。 のextended solutionという。 この時、変数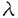 をS1に制限することにより、 をS1に制限することにより、 を を から から U(n)への写像と思うことができ、更に(1)の形より U(n)への写像と思うことができ、更に(1)の形より は は U(n)への正則写像となる。 U(n)への正則写像となる。 が単連結であれば、(1)の積分可能条件が実は が単連結であれば、(1)の積分可能条件が実は の調和性と同値になる。 の調和性と同値になる。 =S2の時は、更に次のことがわかっている。 =S2の時は、更に次のことがわかっている。 事実1(Uhlenbeckによる。1989年)  :S2→U(n)を調和写像とする。このとき :S2→U(n)を調和写像とする。このとき に対し、次をみたす(1)の解 に対し、次をみたす(1)の解 が存在する。 が存在する。 (i) は は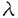 に関し、あるkが存在して に関し、あるkが存在して の形に展開される。 の形に展開される。 (ii) 、但しQはU(n)のある定数元。 、但しQはU(n)のある定数元。 (iii) 。 。  に対し、 に対し、 は は の基点での値の選び方だけ自由度がある。 の基点での値の選び方だけ自由度がある。 定義(Uhlenbeckによる。1989年) 調和写像 : : →U(n)で、そのextended solution →U(n)で、そのextended solution  2が事実1(i)の様に 2が事実1(i)の様に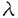 に関し有限項 に関し有限項 に展開されるとき、kの最小値を に展開されるとき、kの最小値を の(最小)ユニトン数((minimal)uniton number)、そのとき の(最小)ユニトン数((minimal)uniton number)、そのとき またはその またはその をk-ユニトン(k-uniton)という。 をk-ユニトン(k-uniton)という。 そこで次が問題となる。 問題:最小ユニトン数はどんな幾何学的意味を持つのか。 それについて知られている事実を述べる前に、次のことに注意する。Grt(Cn)でグラスマン多様体、つまりCn内のt次元部分空間全体のなす空間を表す。Grt(Cn)は計量まで込めて自然にU(n)に埋め込めることが知られている。その埋め込み方は、V∈Grt(Cn)に対し を対応させるものである。(但し、 を対応させるものである。(但し、 VはCnから部分空間Vへの直交射影。)ところで、調和写像とこの埋め込みの合成はやはり調和写像なので、Grt(Cn)への調和写像はU(n)への調和写像で特に像がGrt(Cn)に含まれるもの、と思うことができる。 VはCnから部分空間Vへの直交射影。)ところで、調和写像とこの埋め込みの合成はやはり調和写像なので、Grt(Cn)への調和写像はU(n)への調和写像で特に像がGrt(Cn)に含まれるもの、と思うことができる。 事実2(Uhlenbeckによる。1989年) S2からU(n)への調和写像の最小ユニトン数はn-1以下である。また、0-ユニトンの空間はリーマン面からU(n)への定数写像の空間に一致し、1-ユニトンの空間は、U(n)の定数元の左からの作用を除いてリーマン面からグラスマン多様体Grt(Cn)への正則写像と反正則写像の空間に一致する。 また、調和写像の最小ユニトン数が2となる十分条件が知られている。 定義(Erdem-Woodによる。1983年) 滑らかな写像 : : →Grt(Cn)が等方的(isotropic)であるとは、任意の →Grt(Cn)が等方的(isotropic)であるとは、任意の の正則座標(U,z)、x∈U、a,b∈Nに対し、 の正則座標(U,z)、x∈U、a,b∈Nに対し、  が成り立つことである。但し、 、 、  ( ( はGrt(Cn)のtautoligical束)である。 はGrt(Cn)のtautoligical束)である。 事実3(Bergvert-Guest、酒川による。1992年) 等方的でかつ正則でも反正則でもない調和写像 : : →Grt(Cn) →Grt(Cn) U(n)は2-ユニトンである。 U(n)は2-ユニトンである。 この事実の系として、Segalの結果、つまり射影空間CPn-1に像をもつ正則でも反正則でもない調和写像は2-ユニトンであるという結果もでる。 この論文では逆に、特にS2からU(4)への調和写像でGrt(C4)に像をもつ調和写像のクラスをユニトン数で分類した。事実2により、この場合の最小ユニトン数は0、1、2あるいは3のどれかである。この論文の主定理を述べ、続けて主定理に現れる言葉の定義、解説を行う。以下、グラスマン多様体への写像 と、 と、 を同一視する。また、直交する束同士のWhitney和を を同一視する。また、直交する束同士のWhitney和を で表す。 で表す。 主定理 S2からGr2(C4) U(4)への調和写像全体の空間は、等方性とユニトン数により次のように分類される。 U(4)への調和写像全体の空間は、等方性とユニトン数により次のように分類される。 i)等方的な場合; 1)0-ユニトンは定数写像のみである。 2)1-コニトンは正則あるいは反正則写像のみである。 3)2-ユニトンは、次のうちのどれかとなる。 ・CP2への非正則・非反正則な調和写像fと、S2上の自明直線束cが存在して、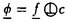 と分解される写像 と分解される写像 。 。 ・Frenet pair。 ・Frenet pairを1回froward replacementして得られる写像で、非正則・非反正則なもの。 ・等方的なmixed pair。 ・等方的なmixed pairを1回forward replacementして得られる写像で非正則・非反正則なもの。 4)3-ユニトンはない。 ii)等方的でない場合; 1)0,1-ユニトンはない。 2)2-ユニトンは等方的でないmixed pairのみである。 3)3-ユニトンは、等方的でないmixed pairを1回forward replacementして得られる写像のみである。 まず、 からGrt(Cn)への調和写像の中では簡単な構成法でつくることのできる、Frenet pairとmixed pairの定義を行う。 からGrt(Cn)への調和写像の中では簡単な構成法でつくることのできる、Frenet pairとmixed pairの定義を行う。 と と を、 を、 からグラスマン多様体への写像で、 からグラスマン多様体への写像で、 と と が直交するものと仮定する。 が直交するものと仮定する。 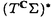 の切断である第2基本形式 の切断である第2基本形式 、 、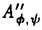 を、 を、 の切断sに対し の切断sに対し  で定義する。(但し は は から から へのエルミート射影。) へのエルミート射影。) 、 、 とおく。 とおく。 が調和写像である必要十分条件は が調和写像である必要十分条件は (または (または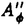 )が正則(または反正則)切断であることである。正則切断 )が正則(または反正則)切断であることである。正則切断 に対しては、唯一 に対しては、唯一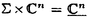 の正則部分束 の正則部分束 で、 で、 の高々孤立点上のファイバーを除いてImage of の高々孤立点上のファイバーを除いてImage of  と一致するものが存在する。同様に と一致するものが存在する。同様に も定義できる。 も定義できる。 とおき、 とおき、 のガウス束と呼ぶ。G’( のガウス束と呼ぶ。G’( )が定義する )が定義する からGrt’(Cn)への写像も調和写像となるので、順にG(k)( からGrt’(Cn)への写像も調和写像となるので、順にG(k)( ):=G’(G(k-1)( ):=G’(G(k-1)( ))(k>0)と定義でき、(k番目の)ガウス束と呼ぶ。同様に、 ))(k>0)と定義でき、(k番目の)ガウス束と呼ぶ。同様に、 、G(-k)( 、G(-k)( ):=G"(G(-k+1)( ):=G"(G(-k+1)( ))(k>0)と定義する。 ))(k>0)と定義する。 定義(Bustall-Woodによる。1986年) f: →CPn-1を正則写像、g: →CPn-1を正則写像、g: →CPn-1を反正則写像とする。 →CPn-1を反正則写像とする。 とおくと とおくと は調和写像となるが、これをFrenet pairと呼ぶ。また、 は調和写像となるが、これをFrenet pairと呼ぶ。また、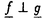 かつ かつ のとき のとき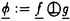 とおくと とおくと は調和写像になるが、これをmixed pairと呼ぶ。 は調和写像になるが、これをmixed pairと呼ぶ。 ここでついでに、主定理の中に現れる等方的なmixed pairとはどのようなものであるか述べておく。 命題 Mixed pair  :S2→Gr2(Cn)が等方的である必要十分条件は、 :S2→Gr2(Cn)が等方的である必要十分条件は、  である。 Forward replacementとは、次のような調和写像の空間内の変換である。 定義(Burstall-Woodによる。1986年)  : : →Grt(Cn)を調和写像とする。 →Grt(Cn)を調和写像とする。 の正則部分束 の正則部分束 で で  を満たすものに対し、 を満たすものに対し、 とおくと、F( とおくと、F( , , )は )は からあるグラスマン多様体への調和写像となる。 からあるグラスマン多様体への調和写像となる。 からF( からF( , , )をつくる手順をforward replacementと呼ぶ。同様に、上の定義で )をつくる手順をforward replacementと呼ぶ。同様に、上の定義で を反正則部分束、∂を用いているところをすべて を反正則部分束、∂を用いているところをすべて に換えて得られる写像をB( に換えて得られる写像をB( , , )と書き、 )と書き、 からB( からB( , , )を得る手順をbackward replacementと呼ぶ。 )を得る手順をbackward replacementと呼ぶ。 主定理の証明のあらすじを述べよう。途中のほとんどの計算は、一般のリーマン面 から一般のグラスマン多様休Grt(Cn)への調和写像に対して成り立つ。 から一般のグラスマン多様休Grt(Cn)への調和写像に対して成り立つ。 S2からU(n)への各調和写像に対し、extended solution  であって であって を満たすもの(normalized extended solution)が唯一存在し、しかもこの を満たすもの(normalized extended solution)が唯一存在し、しかもこの のkが最小ユニトン数となることが知られている。よって、ユニトン数を求めるのに、各調和写像のnormalized extended solutionを具体的に求めればよい。ところで次が知られている。 のkが最小ユニトン数となることが知られている。よって、ユニトン数を求めるのに、各調和写像のnormalized extended solutionを具体的に求めればよい。ところで次が知られている。 事実4(Burstall-Woodによる。1986年) 調和写像 :S2→Gr2(Cn)に対し、次のような調和写像の列 :S2→Gr2(Cn)に対し、次のような調和写像の列 0,…, 0,…, N:S2→Gr2(Cn)が存在する。 N:S2→Gr2(Cn)が存在する。 (1) 0= 0= 、 、 Nは正則写像、Frenet pairまたはmixed pairである。 Nは正則写像、Frenet pairまたはmixed pairである。 (2) i-1は i-1は iからforward replacementまたはbackward replacementで得られる。 iからforward replacementまたはbackward replacementで得られる。 まず実際に、Frenet pairやmixed pairのextended solutionを求めると、そのtop termが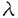 2となることから、事実2とも合わせてこれらが2-ユニトンであることがわかる。それから、事実3より、等方的な調和写像のユニトン数はわかっていた。よって我々は、Frenet pairが等方的であること、等方的調和写像をforward replacementしたものは等方的であることを、Salamonによって導入されたflagのdiagrainという概念を使って証明する。等方的でないmixed pairをforward replacementしてできる調和写像のextended solutionは、一般的にforward replacementに対応しextended solutionがどのように変化するか具体的に記述する事により求めることができるが、こうやって求めたものは、normalized extended solutionとは限らない。よって、それに適当な 2となることから、事実2とも合わせてこれらが2-ユニトンであることがわかる。それから、事実3より、等方的な調和写像のユニトン数はわかっていた。よって我々は、Frenet pairが等方的であること、等方的調和写像をforward replacementしたものは等方的であることを、Salamonによって導入されたflagのdiagrainという概念を使って証明する。等方的でないmixed pairをforward replacementしてできる調和写像のextended solutionは、一般的にforward replacementに対応しextended solutionがどのように変化するか具体的に記述する事により求めることができるが、こうやって求めたものは、normalized extended solutionとは限らない。よって、それに適当な U(n)の元をかけて実際にnormalized extended solution U(n)の元をかけて実際にnormalized extended solution  を構成する。このときの を構成する。このときの のtop termが のtop termが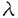 3であることがわかるから、ユニトン数3がわかる。調和写像の行き先の多様体がGr2(C4)のときには、事実4に現れる調和写像の列の長さNがN=0または1となること、更にそのとき 3であることがわかるから、ユニトン数3がわかる。調和写像の行き先の多様体がGr2(C4)のときには、事実4に現れる調和写像の列の長さNがN=0または1となること、更にそのとき 1はFrenet pairまたはmixed pairになり、 1はFrenet pairまたはmixed pairになり、 0は 0は 1からforward replacementにより得られることを、やはりdiagramを使って示すと、主定理の証明が終わる。 1からforward replacementにより得られることを、やはりdiagramを使って示すと、主定理の証明が終わる。 主定理の系としては次がわかる。 系 S2からGr2(C4)への調和写像でユニトン数が2であるものは、等方的調和写像あるいはmixed pairに限る。 これは、S2からGr2(C4)への調和写像に話を限定したときには、事実3で得られた結果以外にユニトン数が2のものはmixed pairしかないことを示している。 |