| 内容要旨 | | 本論文の目的は,複素構造をかえながら動くリーマン面上の微分方程式(正確には,正則または有理形の射影接続)のモジュライの上に定義される自然な(退化した)シンプレクティック構造の性質を明きらかにすることである。このような問題意識の背景にあるのは,複素領域における線形常微分方程式のモノドロミー保存変形の理論である。今世紀初めに,R.Fuchs,L.Schlesinger,R.Garnierの三氏らは,リーマン球面P1上の2階(または1階)の線形常微分方程式(系)のモノドロミー保存変形を考察して,変形方程式としてパンルヴェ方程式I-VIを導出した。岡本和夫氏は,1970年代に入り,リーマン面がトーラス(種数=1)の場合にこれと同様の考察を行って,パンルヴェ方程式の一つの一般化を得る一方で,P1上での2階の方程式のモノドロミー保存変形が,変形のパラメーターに関する可積分ハミルトン系として記述されるという重要な事実を見出した。(後にこれはトーラス上での場合にも同氏によって確かめられた。)この事実を,一般の種数のリーマン面に対して示したのは岩崎克則氏である。彼はコンパクトリーマン面上のフックス型の有理形射影接続のモジュライを実際に構成し,適当な座標をとることによって,モノドロミー保存変形をラグランジアン葉層として記述するような閉2形式を具体的にかき下すことに成功した。我々にとって最も重要な方法論的出発点となったのは,同じく岩崎氏によって示された,次の事実である。 定理(岩崎):上述の閉2形式は,(特異点に対応する)点を抜いたリーマン面の基本群の表現類の空間(ただし抜いた点のまわりの局所的な表現は固定されているとする)の上に定義される自然なシンプレクティック形式の,モノドロミー写像による引き戻しにちょうど一致する。 実際,シンプレクティック形式は非退化であるから,(もしモノドロミー写像が微分のレベルで全射であれば),引き戻しによって得られた閉2形式は完全にモノドロミー保存変形を記述することになる。これにより我々は, 《微分方程式のパラメーターの空間の上にモノドロミー写像を通じて定義される(退化した)シンプレクティック構造を調べることによりモノドロミー保存変形を考察する》 という基本的原理を得ることになったのである。 これらの研究の成果をふまえて,本論文では扱う状況をさらに一般にして,リーマン面の複素構造をも動かしながら微分方程式のモノドロミー保存変形を考察する。第一部では,リーマン面がトーラスの場合にフックス型の有理形射影接続に対応する微分方程式を扱う。Xを種数1のリーマン面,Hを上半平面としよう。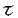 ∈Hをとり,X=C/Z・1 ∈Hをとり,X=C/Z・1 Z・ Z・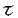 と表せば,X上の方程式はC上の方程式であって係数が二重周期関数となるものとして表現される。 と表せば,X上の方程式はC上の方程式であって係数が二重周期関数となるものとして表現される。  なる形の方程式は,z≡ti(mod Z・1 Z・ Z・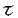 )に確定特異点(特性指数の差は )に確定特異点(特性指数の差は i)をもつフックス型方程式であり, i)をもつフックス型方程式であり,  によってパラメトライズされる。ここで, i∈Cは定数とみなすこととし,特異点z≡tiは対数的でないとする。また, i∈Cは定数とみなすこととし,特異点z≡tiは対数的でないとする。また,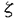 (z, (z,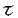 ), ),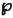 (z, (z,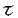 )は基本周期1, )は基本周期1,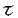 のワイエルシュトラスの のワイエルシュトラスの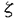 -関数, -関数,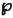 -関数であり, -関数であり,  とする。このとき,方程式(1)のモノドロミー保存変形を記述する閉2形式の具体的な形を示すのが第一部の主定理である。 定理1:求める閉2形式は次のように表される。  2形式(2)が閉形式となることは,第3項を とかき直すことによりすぐわかる。また,この2形式が方程式(1)のパラメーターの自然な変換で不変となることも確かめられた。さらに(2)の形から,もし方程式(1)のモノドロミー保存変形を固定されたトーラスの上で考えれば,得られる閉2形式は とかき直すことによりすぐわかる。また,この2形式が方程式(1)のパラメーターの自然な変換で不変となることも確かめられた。さらに(2)の形から,もし方程式(1)のモノドロミー保存変形を固定されたトーラスの上で考えれば,得られる閉2形式は  となることもわかる。実際,これは岡本氏と岩崎氏によって既に得られていたものと一致している。 以上の結果を一般の種数のリーマン面上での場合に拡張することが第二部の目標である。(ただし特異点は考えないことにする。)トーラス上で考える場合には,微分方程式を具体的に表示することができたので,求める閉2形式も明示的にかき下すことができた。しかし今回は,より間接的な方法で《微分方程式のモジュライ》を考察することになる。Xを種数g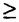 2のリーマン面,Hを先と同様に上半平面としよう。一意化定理によりフックス群 2のリーマン面,Hを先と同様に上半平面としよう。一意化定理によりフックス群 をとって,X=H/ をとって,X=H/ と表すことができる。すると,リーマン面X上の(正則)射影接続の全体は,H上の と表すことができる。すると,リーマン面X上の(正則)射影接続の全体は,H上の に関する正則二次微分全体のなすベクトル空間A2(H, に関する正則二次微分全体のなすベクトル空間A2(H, )と同一視されることになる。q∈A2(H, )と同一視されることになる。q∈A2(H, )に対して,H上での方程式 )に対して,H上での方程式  の任意の解fは,Hからリーマン球面P1への局所双正則写像となり,  によって準同型 : : →PSL(2,C)を定める。(3)の解の一般形はAof(A∈PSL(2,C))と表され,対応する準同型は →PSL(2,C)を定める。(3)の解の一般形はAof(A∈PSL(2,C))と表され,対応する準同型は  A A ( ( )A-1の形であるから,各q∈A2(H, )A-1の形であるから,各q∈A2(H, )に対して表現 )に対して表現 →PSL(2,C)の共役類が一つ定まることになる。これが二次微分qの(またはqに対応するX上の射影構造の)モノドロミーにほかならない。 →PSL(2,C)の共役類が一つ定まることになる。これが二次微分qの(またはqに対応するX上の射影構造の)モノドロミーにほかならない。 次に,リーマン面Xの複素構造を動かして考えるために,(標識付き)フックス群 のタイヒミュラー空間T( のタイヒミュラー空間T( )と普遍タイヒミュラー曲線 )と普遍タイヒミュラー曲線 :V( :V( )→T( )→T( )を導入しよう。各 )を導入しよう。各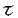 ∈T( ∈T( )に対して,擬半平面 )に対して,擬半平面 と擬フックス群 と擬フックス群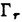 が対応し,射影 が対応し,射影 の の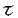 上のファイバーは 上のファイバーは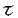 の表す標識付きリーマン面 の表す標識付きリーマン面 / /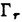 となる。各 となる。各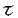 に対して, に対して, 上の 上の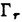 に関する正則二次微分全体をA2( に関する正則二次微分全体をA2( , ,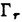 )とすれば,これらの全体は正則ベクトル束Q→T( )とすれば,これらの全体は正則ベクトル束Q→T( )を形成し,したがって全空間Qは複素構造をかえながら動くリーマン面上の射影接続のモジュライとみなされることになる。さらに,各q∈A2( )を形成し,したがって全空間Qは複素構造をかえながら動くリーマン面上の射影接続のモジュライとみなされることになる。さらに,各q∈A2( , ,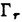 )が表現 )が表現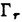 →PSL(2,C)の共役類を一つ定めることから,結局モノドロミー写像 →PSL(2,C)の共役類を一つ定めることから,結局モノドロミー写像  が,自然な同型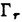 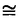  を通じて定義されることになる。写像Fについての基本的事実として,(1)ImFの各点はRの正則点であり,(2)Fは局所双正則写像となることが知られている(D.Hejhal,C.Earle,J.Hubbard氏らによる)。 を通じて定義されることになる。写像Fについての基本的事実として,(1)ImFの各点はRの正則点であり,(2)Fは局所双正則写像となることが知られている(D.Hejhal,C.Earle,J.Hubbard氏らによる)。 先に述べたように,我々の目的は空間R上の自然なシンプレクティック構造 RをFによって引き戻して得られるQ上のシンプレクティック構造を調べることである。ところが一方で,空間Qはタイヒミュラー空間T( RをFによって引き戻して得られるQ上のシンプレクティック構造を調べることである。ところが一方で,空間Qはタイヒミュラー空間T( )の正則余接束T*T( )の正則余接束T*T( )とみなされ,したがってその上には自然なシンプレクティック構造 )とみなされ,したがってその上には自然なシンプレクティック構造 Qが定まることになる。Q上に定まるこれら二つのシンプレクティック構造が(定数倍を除いて)一致することを主張するのが第二部の主定理である。 Qが定まることになる。Q上に定まるこれら二つのシンプレクティック構造が(定数倍を除いて)一致することを主張するのが第二部の主定理である。 定理2:写像F:Q→Rはシンプレクティック構造を(定数- /2を除いて)保つ,すなわち /2を除いて)保つ,すなわち  が成立する。 これによって我々は,(特異点を考えないという制限つきで),射影接続のモジュライの上に引き戻しを通じて定義されるシンプレクティック構造の内在的な特徴づけを与えたことになる。 |
| 審査要旨 | | 本論文の目的は、複素構造を変えながら動くリーマン面上の微分方程式(正確には、正則または有理形の射影接続)のモジュライの上に定義される自然な(退化した)シンプレティック構造の性質を明らかにすることである。このような問題の背景には、複素領域における線形常微分方程式のモノドロミー保存変形の理論がある。 今世紀初めに、R.Fuchs,L.Schlesinger,R.Garnier等は、P1上の2階(または1階)の線形常微分方程式(系)のモノドロミー保存変形を考察して、変形方程式としてパンルヴェ方程式I-VIを導出した。 1970年代には、岡本和男氏は、トーラス(種数=1)の場合に同様の考察を行って、パンルヴェ方程式の一つの一般化を得た。また、P1上での2階の方程式のモノドロミー保存変形が、変形パラメーターに関する可積分ハミルトン系として記述されるという重要な事実を発見し、後にトーラスの場合に同氏によって確かめられた。 岩崎克則氏はこの事実を、一般の種数のリーマン面に対して示した。彼はコンパクトリーマン面上のフックス型の有理射影接続のモジュライを実際に構成して、モノドロミー保存変形をラグランジアン葉層として記述する具体的閉2形式を与えた。 この閉2形式は、特異点に対応する点を抜いたリーマン面の基本群の表現類の空間(ただし抜いた点のまわりの局所的な表現は固定されているとする)の上に定義される自然なシンプレクティック形式の、モノドロミー写像による引き戻しに一致する。 これらのことから微分方程式のパラメーターの空間の上にモノドロミー写像を通じて定義される(退化した)シンプレティック構造を調べることによりモノドロミー保存変形を考察することができる。 本論文では、とり扱う状況を更に一般化して、リーマン面の複素構造をも動かしながら微分方程式のモノドロミー保存変形を考察している。 第一の結果は、リーマン面がトーラスの場合のフックス型の有理形射影接続に対応する微分方程式に関するものである。 Xを種数g=1のリーマン面、1,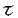 を基本周期とする。X上の方程式はC上の方程式であって係数が二重周期関数となるものである。 を基本周期とする。X上の方程式はC上の方程式であって係数が二重周期関数となるものである。 なる形の方程式は、z≡ti(mod Z.1+Z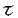 )に確定特異点を持つフックス型方程式で、k,Hi,ti, )に確定特異点を持つフックス型方程式で、k,Hi,ti,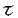 によってパラメトライズされる。ここでは、 によってパラメトライズされる。ここでは、 iは定数としておき、特異点z≡tiは対数的でないとする。このとき、方程式(1)のモノドロミー保存変形を記述する閉2形式は iは定数としておき、特異点z≡tiは対数的でないとする。このとき、方程式(1)のモノドロミー保存変形を記述する閉2形式は である与えられる。 この閉2形式は、方程式(1)kパラメーターの自然な変換で、もしモノドロミー保存変形を固定されたトーラスの上で考えれば、初項のみより成る閉2形式が得られ、これは岡本氏と岩崎氏によって既に得られているものと一致している。 次の結果は一般の種数のリーマン面上の場合に対応するものである。 Xを種数gのリーマン面、Hを上半平面、 をフックス群としてX=H/ をフックス群としてX=H/ とする。X上の射影接続の全体は、H上の とする。X上の射影接続の全体は、H上の に関する正則二次微分全体のなすベクトル空間A2(H, に関する正則二次微分全体のなすベクトル空間A2(H, )と同一視される。q∈A2(H, )と同一視される。q∈A2(H, )に対して、H上での方程式 )に対して、H上での方程式 の任意の解fは、 によって準同型 : : →PSL(2,C)が定まる。解の一般形の考察から、二次微分にはその共役類が定まる、これがqに対応する射影構造のモノドロミーである。 →PSL(2,C)が定まる。解の一般形の考察から、二次微分にはその共役類が定まる、これがqに対応する射影構造のモノドロミーである。 リーマン面の複素構造を動かして考える。タイヒミュラー空間T( )の元 )の元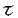 に対応する標識付きリーマン面を考え、対応する概念としてモノドロミー写像 に対応する標識付きリーマン面を考え、対応する概念としてモノドロミー写像 を得る。ここにQは複素構造を変えながら動くリーマン面上のモジュライの全体である。Fが局所双正則写像であることはD.Hejhal,C.Earle,J.Hubbard氏らによる。 空間Q上にはタイヒミュラー空間T( )の正則余接束として自然なシンプレティック横造 )の正則余接束として自然なシンプレティック横造 Qがある。これとR上の自然なシンプレティック構造のFによる引き戻しとは(定数倍を除いて)一致するというのが第二の主張である。つまり、 Qがある。これとR上の自然なシンプレティック構造のFによる引き戻しとは(定数倍を除いて)一致するというのが第二の主張である。つまり、 これによって射影接続のモジュライの上に引き戻しを通じて定義されるシンプレティック構造の内在的特徴づけを与えている。 これらの結果はこの方面の研究に本質的な新しい知見と手法を提供するものである。 よって、論文提出者河井真吾は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |