代数体k上の簡約代数群Gに対し、Gのアデール化をG(A),k有理点の群をG(k)とする。商空間(G(k)\G(A))上のに二乗可積分関数の空間L2(G(k)\G(A))におけるG(A)の右正則表現は既約表現の可算和と連続和に分解される。この既約成分は保型表現と呼ばれ、それらを決定することは保型形式論の窮極の目標であるとは言え、また困難な問題であることは一般に認識されている。最も古典的な場合でさえ、素朴な意味の解決は期待されない。このことはかえって他の研究対象との関連を重視させ、その関連が例えばL関数を媒介として具体的に述べられることにより、理論の厚みを増したと考えることができる。 本論文はkの2次拡大体k’に対し定義される階数2のquasi-spritなユニタリ群G=U(2,2)を取り上げて、その剰余スペクトルすなわちL2(G(k)\G(A))の離散スペクトルに含まれるが、尖点形式では生成されない既約成分をすべて決定している。 一般に上記のL2空間はGの放物型部分群とそのLevi部分群の尖点表現から定義されるEisenstein級数で生成され、それらのL2空間における内積は、ある系列の表現とその反傾表現との間の内積の積分和の形に書かれている。本論文で考察する場合には、積分のパラメーターは放物型部分群の階数に従って、復素平面または復素平面二つの直積の中の積分路を動く。積分路を、積分される表現がユニタリとなる位置まで移動するとき、特異点を横切るごとに留数として次元が一つだけ小さい積分和か現れる。このようにして最終的に留数として分離される既約表現が求める剰余スペクトルである。 以上のプログラムはLang’lands理論により知られているとは言え、剰余スペクトルを特定することは決して自明な問題ではない。それは、ある種の保型L関数の特異点を調べることと、ある誘導表現の既約成分を具体的に記述することに帰着されるが、ここは階数2の代数群の保型表現に関する既知の結果を総動員する感があり、それに論文提出者の創意と精密な議論を加えて主定理を得るのである。 主定理の詳細は論文本文にゆずり、ここではG=U(2,2)の剰余スペクトルの定性的分類のみを述べる。 Gの標準放物型部分群をP0,P1,P2,それらのLevi部分群を,M1=ResGL(2),M2=ResGL(1)×U(1,1)とする。ただしResはk’からkへの係数体の制限を表す。 このときGの剰余スペクトルは次のとおり分類される。各々の重複度は1である。 (1)1次元表現 (2)1次ユニタリ群U(V,A)の単位表現の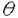 -lift -lift (3)2次ユニタリ群U(1,1)(A)の非自明な1次元表現の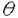 -lift -lift (4)M1(A)=GL2(Ak’)のある種の’distinguished’な尖点表現をP1(A)に延長し、それから誘導されるG(A)の表現の既約商 (5)M2(A)= ×U(1,1)(A)の尖点表現X ×U(1,1)(A)の尖点表現X  をP2(A)に延長し、それから誘導されるG(A)の表現の既約商。ただし をP2(A)に延長し、それから誘導されるG(A)の表現の既約商。ただし 1Ax=||A1または|| 1Ax=||A1または||  ( ( は2次拡大k’/kに対応するkの量指標)。第一の場合 は2次拡大k’/kに対応するkの量指標)。第一の場合 は任意であるが、第二の場合 は任意であるが、第二の場合 はU(1)(A)の1次元表現の はU(1)(A)の1次元表現の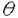 -lift -lift M1,M2の尖点表現は良く研究された対象である。本論文の結果が剰余スペクトルの性質について確かな知見を加えたことは高く評価することができる。 よって論文提出者今野拓也は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |