| 内容要旨 | | 1序 多様体Dの上で定義された線型微分方程式系(M)の解が,適当なパラメータ空間X上の函数の積分変換によって具体的に構成されるような状況を考えよう(重ね合わせの原理)。非常に良い状況では,(M)の大城解の空間Sol(M)⊂C∞(D)はパラメータ空間X上の函数空間のある積分変換の像として記述できる場合がある。例えば,D=単位円板,Sol(M)={f∈C∞(D): f=0}=(単位円板の調和函数の空間)とする時,ポアソン変換によって,Sol(M)はパラメータ空間X=S1上の超函数B(S1)の像として得られる。この一般化はリーマン対称空間に対するHelgason予想(定理)として知られている。 f=0}=(単位円板の調和函数の空間)とする時,ポアソン変換によって,Sol(M)はパラメータ空間X=S1上の超函数B(S1)の像として得られる。この一般化はリーマン対称空間に対するHelgason予想(定理)として知られている。 この論文の主要テーマは,  とした時,X上の函数空間(正確には,あるDolbaultコホモロジーの空間)から(Mk)の解空間Sol(Mk)⊂O(D)への写像(ペンローズ変換)を定義し,その全単射性を証明することである。 表現論の立場からは,我々の主結果は 1)U(n,n)の特異な無限小指標を持つ既約ユニタリ最高ウェイト表現のDolbealtコホモロジーによる実現から,有界対称領域上の正則line bundleの正則切断の空間(=既約とは限らないstandard modules)への,intertwining operator(ペンローズ変換)を具体的に構成し, 2)さらにその像を微分方程式で特徴づける。 という意味をもつ。この結果の原型となるのは半単純リー群の離散系列表現が,リーマン対称空間上の一階の楕円型微分方程式(Schmid作用素)の解空間として実現できるというSchmid,Hotta-Parthasarathyの結果である。彼らの設定では,無限小指標が十分に非特異であり,複素多様体X=G/LにおいてLはコンパクトトーラスであるという2つの仮定が使われているが,いずれも我々の設定では満たされていない。特に無限小指標が特異であるという我々の設定においては, 3)Schmid作用素に相当するCauchy-Riemann方程式に加えて高次の微分方程式系(Mk)が現れること が新しい発見の一つである。 主結果を正確に述べるために,以下の準備をしよう。 2.複素多様体U(n,n)/U(k)×U(n-k,n) 複素グラスマン多様体Grk(C2n)は,C2nのk-次元部分空間の全体のなすk(2n-k)-次元のコンパクト複素多様体である。一般線型群GL(2n,C)は,C2nに線型に作用するので,グラスマン多様体Grk(C2n)にも自然に作用する。この作用は推移的であり,従ってグラスマン多様体Grk(C2n)は,GL(2n,C)の等質多様体となる。さて,C2nに不定値エルミート計量  を入れる。この不定値エルミート計量を制限したとき,正定値となるようなk-次元部分空間全体(1 k k n)は,グラスマン多様体Grk(C2n)の中で開集合Xn,kとなる。計量(,)を不変にする不定値ユニタリ群U(n,n)は,Xn,kに推移的に作用し,Xn,kは,等質多様体 n)は,グラスマン多様体Grk(C2n)の中で開集合Xn,kとなる。計量(,)を不変にする不定値ユニタリ群U(n,n)は,Xn,kに推移的に作用し,Xn,kは,等質多様体  と表される。n=1,k=1の場合は,  というよく知られたBorel埋め込みに対応する。また,n=kの場合には,Xn,kは,極大放物型部分群のBruhat分解を用いることにより,古典型有界対称領域  として実現される。 3.同伴正則LINE BUNDLEのDOLBEAULTコホモロジー 複素多様体Xn,k=U(n,n)/U(k)×U(n-k,n)≡G/L(k)上に,一次元表現(det)n 1:U(k)×U(n-k,n)→C×に同伴した正則line bundleを 1:U(k)×U(n-k,n)→C×に同伴した正則line bundleを で表す。この正則line bundle で表す。この正則line bundle 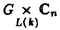 に係数を持つDolbeaultコホモロジー に係数を持つDolbeaultコホモロジー には自然にFrechet位相が入ることを,表現論的手法により,Schmid,Wongが最近証明した(1992年)。Dolbeaultコホモロジー には自然にFrechet位相が入ることを,表現論的手法により,Schmid,Wongが最近証明した(1992年)。Dolbeaultコホモロジー はj≠k(n-k)のとき0となり,j=k(n-k)では無限次元となる(1 はj≠k(n-k)のとき0となり,j=k(n-k)では無限次元となる(1 k k nとする)。 nとする)。 一方,有界対称領域Xn,n=D上に|I|=|J|次の微分作用素P(I,J)を  で定義する。ここで,I,Jは{1,…,n}の部分集合でIとJの個数が等しいものとする。次に,D上の線型微分方程式系(Mk)を  と定義し,その正則な大域解の空間を 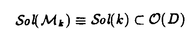 とおく。 また,Dのglobalな座標によって,O(D)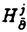  を同一視すると, を同一視すると,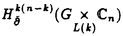 へのG=U(n,n)の作用によって,O(D)にkに依存した表現(standard modules)を定義することができる。この意味でSol(Mk)⊂O(D)はGの不変部分空間である。一方, へのG=U(n,n)の作用によって,O(D)にkに依存した表現(standard modules)を定義することができる。この意味でSol(Mk)⊂O(D)はGの不変部分空間である。一方, もGのFrechet表現である。この時,次の主定理を得た。 もGのFrechet表現である。この時,次の主定理を得た。 主定理.0)G=U(n,n)とする。k=0,1,2,...,nに依存したGの部分群をL(k)=U(k)×U(n-k,n)で定義する。このときFrechet G-加群からFrechet G-加群への連続なG-準同型写像(ペンローズ変換)  が定義される。 1)Rは単射である。 2)Rの像は,有界対称領域D上で,定義された偏微分方程式系(Mk)およびCauchy-Riemann方程式の解空間Sol(Mk)に含まれる。 3)Rは,Dolbeaultコホモロジー と解空間Sol(Mk)の各々のK-有限ベクトルのなす空間上の全単射写像を誘導する。特に,Rの像はSol(Mk)で稠密である。 と解空間Sol(Mk)の各々のK-有限ベクトルのなす空間上の全単射写像を誘導する。特に,Rの像はSol(Mk)で稠密である。 なお,Schmidのmaximal globalizationの結果を援用すれば,  という結果が(3)から直ちに導かれることに注意しておく。 またGindikinは,東京大学の集中講義(1994年)において,積分幾何の手法を用いて,n=2,k=1の時Rの逆写像の構成を行うことにより,Rの全射性を証明した。 我々の全射性の証明は別の方法を用いた。すなわち,Blattnerの公式を援用した上で,最高ウェイトベクトルの満たす微分方程式系を(Mk)に連立させた方程式系を考察する。参考論文では半単純対称空間上の不変微分作用素についてCartan分解に付随した動径成分をルート系の議論によって直接の計算で求めたが,上記の方程式系の解の性質を調べるためには(別の種類の)微分作用素についてBruhat分解に付随した動径成分を具体的に決定するという手法をとった。 |
| 審査要旨 | | 半単純リー群Gの表現は、Harish-ChandraがGにおけるPlancherelの公式を得て以来、Knapp-Zuckermanによるtemperedな表現の分類、Langlandsによる既約認容表現の分類、ZuckermanのDerived functor moduleによる表現の構成や旗多様体上のD-加群を用いた表現の分類、などにより一般の表現の構造が解明されて来た。これらにより、十分regularな表現は、その性質がよく分かるようになり、singularな表現を解明することが半単純リー群の表現論での現在最も重要なテーマとなっている。 Gの表現は、Borel-Weil-Bottによる有限次元表現の構成、主系列表現、Derived functor module、D-加群による構成、というようなGの"境界"上の関数やベクトル束、あるいはそのCohomology空間に構成する方法と、行列要素を考えることにより、群や対称空間、あるいは、そこの上のベクトル束の切片に構成する方法とに大別される。表現の既約性やその性質を研究するには、この2つの構成の間の関連を調べる事が極めて有効である。また、それぞれ自然に実現されている場合は、幾何学的問題や解析における境界値問題などと関連して種々の解釈がなされ、他の分野と関連して重要な例を提供して来た。 Derived functor moduleによる代数的な表現の構成は、Gの複素化の一般旗多様体におけるGの開軌道上の正則線形束に係数を持つDolbeault Cohomologyとして解析的に自然に定義され、Frechet位相が入ることが、最近SchmidとWongにより、証明された。 論文提出者関口英子は、Gを不定値ユニタリ群U(n,n)、一般旗多様体をグラスマン多様体Grk(C2n)として、そこの上の開軌道Xn,k=U(n,n)/U(k)×U(n-k,n)の場合にU(k)×U(n-k)の一次元表現detn 1に同伴した正則線形束LkのDolbeault Cohomology 1に同伴した正則線形束LkのDolbeault Cohomology  (G,Lk)を扱った。 (G,Lk)を扱った。 n=k=1の場合は、Gr1(C2)はRiemann球面で、X1,1は、そこに実現されたPoincare Diskを表し、また、一般のn=kでは、Xn,nは古典型有界対称領域として実現され、提出論文で扱ったXn,kは、これらを含むより一般のRiemannianとは限らない対称空間となる。 Cohomology空間 (G,Lk)は、j=k(n-k)の時のみ残って無限次元空間となり、極めてSingularな興味深いU(n,n)の既約表現となることが知られている。 (G,Lk)は、j=k(n-k)の時のみ残って無限次元空間となり、極めてSingularな興味深いU(n,n)の既約表現となることが知られている。 提出論文では、 (G,Lk)から有界対称領域Xn,n上の正則関数の空間への写像Rを表現論的に定義し、その像の満たす微分方程式系を具体的に構成して、写像がその微分方程式系の正則解全体になることを証明した。 (G,Lk)から有界対称領域Xn,n上の正則関数の空間への写像Rを表現論的に定義し、その像の満たす微分方程式系を具体的に構成して、写像がその微分方程式系の正則解全体になることを証明した。 この写像は、n=2かつk=1の場合は、Penrose変換として知られており、Gindikinは積分幾何の方法を用いて、逆写像を構成し、Rの全射単射性を証明している。一般の場合にこの手法を拡張するの困難であるため、提出論文では、表現論的な以下のような手法を用いている。 まず、Rの単射性を、 (G,Lk)の既約性に帰着させて示す。さらに、 (G,Lk)の既約性に帰着させて示す。さらに、 (G,Lk)を極大コンパクト群の表現に分解して、それの重複度を与えるBlattner公式を用い、また、Xn,n上に構成した微分方程式系の動径成分を具体的に計算して解空間の次元を評価し、両者の比較によって全射性を証明している。 (G,Lk)を極大コンパクト群の表現に分解して、それの重複度を与えるBlattner公式を用い、また、Xn,n上に構成した微分方程式系の動径成分を具体的に計算して解空間の次元を評価し、両者の比較によって全射性を証明している。 Rの像の満たす微分作用素系は、k=1の場合は2階の作用素として知られていたが、提出論文で、Xn,nの実現の大域的な座標を用いて、k+1次の小行列式の形で具体的に与えることに成功しており、それはk+1階の微分作用素系となる。その動径成分と解の各K-成分の計算には、通常使われるCartan分解でなくBruhat分解を用い、prehomogeneous vector spaceのb函数や相対不変式の結果を使う方法を開発した。 微分方程式系の解の空間の元を総て積分表示で与える、というのは基本的問題であるが、表現論の観点で重要な場合に、微分方程式系をきわめて具体的に与えてそれに成功したこの論文の意義は大きく、singularな表現の解析に役立つであろう。また、求められた方程式系は、最近研究の進んできた多変数の超幾何微分方程式の理論と関連しており、ここで開発された手法とともに、応用と発展が期待できる。 よって本論文提出者関口英子は、博士(数理科学)の学位をうけるにふさわしい十分な資格があると認める。 |