| 内容要旨 | | 0.Henselな離散付値体K上の多様体のエタール・コホモロジーにはKの絶対Galois群GK=Gal(Ksep/K)が作用しており,これは数論幾何における基本的な研究対象の一つであるが(但しここでKsepはKの一つの分離閉包である),nearby cycleは,このエタール・コホモロジーを近似するようなspecial fiber上のlocalなobjectであり,やはりGKが作用している. 本論文の目的は,多様体がlog.smooth reductionをもつ場合にこのnearby cycleを完全に計算することであり,より詳しくは,第一に,この場合のnearby cycleへのGKの作用がtameである(すなわちwild inertia group P⊂GKが自明に作用し,この結果nearby cycleは,tame nearby cycleと一致する)ことを示すこと,第二にtame nearby cycleの各点での茎を記述する公式を得ることである. 1.前者についてもう少し詳しく説明するために記号を用意する.Kを上のようにし, をK上有限型のschemeとする.便宜上,以下Kの剰余体は分離閉であることを仮定する.AをKの付置環とし,Xを をK上有限型のschemeとする.便宜上,以下Kの剰余体は分離閉であることを仮定する.AをKの付置環とし,Xを のA上の一つのmodel(すなわち,X×ASpec(K)= のA上の一つのmodel(すなわち,X×ASpec(K)= となるようなA上の有限型のscheme)とする.n となるようなA上の有限型のscheme)とする.n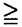 1をAで可逆な整数とする.また 1をAで可逆な整数とする.また をKsep内のKの最大tame拡大とする(ここで,mはAで可逆な全ての整数を走り, をKsep内のKの最大tame拡大とする(ここで,mはAで可逆な全ての整数を走り, はAの一つの素元である.) はAの一つの素元である.) , , でそれぞれX×ASpec(Ktame),X×ASpec(Ksep)をあらわす.このときXに伴うnearby cycleとは,次の式によって定義されるspecial fiber Xs上の でそれぞれX×ASpec(Ktame),X×ASpec(Ksep)をあらわす.このときXに伴うnearby cycleとは,次の式によって定義されるspecial fiber Xs上の 層である.(後の都合のため,tame nearby cycleも同時に定義する.) 層である.(後の都合のため,tame nearby cycleも同時に定義する.)  ここで,qは任意の整数,iはXs→Xというclosed immersionである. さて一般に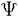 qへのGalois群の作用の複雑さには,Xのreductionの複雑さが反映することが観察される.例えばもしXがgood reductionをもつ(すなわちXがA上smoothである)ならば, qへのGalois群の作用の複雑さには,Xのreductionの複雑さが反映することが観察される.例えばもしXがgood reductionをもつ(すなわちXがA上smoothである)ならば,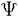 qへのGKの作用は自明であることが,local acyclicityから簡単にわかる.逆にXのreductionが悪いと qへのGKの作用は自明であることが,local acyclicityから簡単にわかる.逆にXのreductionが悪いと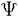 q,ひいては q,ひいては のエタール・コホモロジーへのGKの作用は複雑になる.しかしXのreductionがbadではあっても比較的良いreductionである場合には, のエタール・コホモロジーへのGKの作用は複雑になる.しかしXのreductionがbadではあっても比較的良いreductionである場合には, qにGKの比較的大きい部分が自明に作用する;実際M.RapoportとTh.Zinkとは,以下の(1)(2)の場合に qにGKの比較的大きい部分が自明に作用する;実際M.RapoportとTh.Zinkとは,以下の(1)(2)の場合に (*) qへのPの作用は自明であることを,[RZ]§2,3の中で証明した: qへのPの作用は自明であることを,[RZ]§2,3の中で証明した: (1)Xがgeneralized semistable reductionをもち,その重複度が至るところでA上可逆であるとき. (2)Xがetale localに,semistable curvesの直積のとき. さらに1992年L.Illusieは[I]の中で, (3)Xが二つのsemistable familiesの直積のとき にも(*)が成り立つことを指摘した上で,(*)は,一般に,log.smooth reductionをもつ場合には正しいことが期待できると述べた([I]4.10).但しlog.smooth reductionをもつとは,Xが localにSpec(A[P]/( localにSpec(A[P]/( -x))上 -x))上 ということである.ここでPは有限生成saturatedな可換半群, ということである.ここでPは有限生成saturatedな可換半群, はAの一つの素元,xはPの元で,以下の2条件を満たすものである. はAの一つの素元,xはPの元で,以下の2条件を満たすものである. i)Pgp/〈x〉のtorsion partのorderは,X上可逆である. ii)任意の ∈Pに対し,あるm≧1とb∈Pとがあって,P内でab=xmである. ∈Pに対し,あるm≧1とb∈Pとがあって,P内でab=xmである. 例えば,Xがgeneralized semistable family Spec(A[x1,…,xd]/( … … - - ))で各jについてmj>0である場合には,Xがlog.smooth reductionをもつことと,(m1,…,md)がA上可逆であることとが同値である.従って特に上の(1)の場合はXはlog.smooth reductionをもつことがわかるが,さらに(2),(3)のいずれの場合でもXはlog.smooth reductionをもつことは簡単にわかる. ))で各jについてmj>0である場合には,Xがlog.smooth reductionをもつことと,(m1,…,md)がA上可逆であることとが同値である.従って特に上の(1)の場合はXはlog.smooth reductionをもつことがわかるが,さらに(2),(3)のいずれの場合でもXはlog.smooth reductionをもつことは簡単にわかる. 本論文の主定理の特別な場合である次の結果はこのL.Illusieの問題に対して,肯定的な解決を与えるものである. Theorem(0.1).上の記号の下で,Xがlog.smooth reductionをもつと仮定する.そのとき自然な射  は任意のqに対して同型である.特に qへのKのwild inertia group Pの作用は自明である. qへのKのwild inertia group Pの作用は自明である. Corollary(0.1.1).(0.1)でさらにXがA上properであるとする.そのときPの への作用は自明である. への作用は自明である. 証明は,log.etale cohomologyを用いる.要点は,log.smooth reductionはもちろんgood reductionではないものの,適当なlog.structureをXとAとに付与しlog.schemeとみなすことにより,あたかもgood reductionをもつかのように扱える,ということである.こうして問題をlog.smooth familyについてのlog.etale cohomologyの問題に翻訳することができるが,後者に関しては,あたかも普通のsmooth familyについてのetale cohomologyの問題であるかのように見通しよく議論することができる. 以下証明の概略を述べる.log.smoothnessは,semistabilityとは異なり,base changeによって保たれる.従って,(0.1)は,次のsimpleなlog.etale cohomologyについての定理から,極限に行くことにより,自然に導ける. Theorem(0.2).上の記号の下で,(X,MX)→(Spec(A),the canonical log.str.)をfs log.scheme間のlog.smoothな射とする.ここで,canonical log.str.とは,Spec(A)の閉点によって定義されたlog.structureである. このとき 上の自然な射 上の自然な射  はquasi-isomorphismである,但しjはその上のlog.str.が自明であるようなXの最大のopen subscheme Xtrivからのopen immersionである. (0.2)は,まず,K.FujiwaraおよびK.Katoの結果である,l-進log. cohomologyのlog.blowing-upによる不変性を用いて,generalized semistable reduction X=A[x1,…,xd]/( cohomologyのlog.blowing-upによる不変性を用いて,generalized semistable reduction X=A[x1,…,xd]/( … … - - )の場合に帰着する.次にこの場合には,T.Saitoの議論により,m1+…+mdに関する帰納法が働く.最後にm1+…+md=1のときは,familyはsmoothであり,通常の )の場合に帰着する.次にこの場合には,T.Saitoの議論により,m1+…+mdに関する帰納法が働く.最後にm1+…+md=1のときは,familyはsmoothであり,通常の cohomologyのsmooth base changeによって証明することができる.(miが一つでも0のときは,Xはもはや,上で説明した意味でのlog.smooth reductionではない.実際我々は,(0.1)よりもさらに一般なstatementを証明することになる,というのは(0,2)ではXtriv≠ cohomologyのsmooth base changeによって証明することができる.(miが一つでも0のときは,Xはもはや,上で説明した意味でのlog.smooth reductionではない.実際我々は,(0.1)よりもさらに一般なstatementを証明することになる,というのは(0,2)ではXtriv≠ であるようなX,すなわち,いわゆるhorizontal log.を許すようなXをも同時に扱うことになるからである.) であるようなX,すなわち,いわゆるhorizontal log.を許すようなXをも同時に扱うことになるからである.) 2.さて(0.2)からは,(0.1)とはまた別に,SGA7I3.3-型の の公式を導くこともできる.その公式と先の(0.1)とにより,log.smooth familyのnearby cycleについては十分な理解を得たことになる. の公式を導くこともできる.その公式と先の(0.1)とにより,log.smooth familyのnearby cycleについては十分な理解を得たことになる. 最後に,(0.2)はlog.etale cohomology論内部の定理としてみても興味深い帰結を有しており,例えば,log.smooth族に対してのrelativeなlog.Poincare dualityなどを,(0.2)を用いて証明することができる. REFERENCES[I]Illusie,L.,Expose I Autour du theoreme de monodromie locale,preprint.[RZ]Rapoport,M.and Zink,Th.,Uber die lokale Zetafunktion von Shimuravarietaten.Monodromiefiltration und verschwindende Zyklen in ungleicher Charakteristik,Invent.Math.68(1982),21-201.[SGA7]Grothendieck,A.,Deligne,P.and Katz,N.with Raynaud,M.and Rim,D.S.,Groupes de monodromie en geometrie algebriques,Lect.Notes Math.288,340(1972-73). |
| 審査要旨 | | etale cohomologyはWeil予想解決のため,Grothendieckにより定義された.一方近年Fontaine-Illusie,加藤らは,スキームにある付加構造をつけたlogスキームを研究するlog代数幾何を提唱し,その重要性が明らかになりつつある.中山能力氏はlogスキームのetale cohomologyについて研究を進め,そのPoincare双対性,proper底変換定理など,それが通常のetale cohomologyと同様のよい基本的な性質を満たすことを示していた.本論文ではさらにnearby cycleの層について考察し、log smoothの仮定のもと,それが扱いやすいものであることを示し,その完全な記述を与えた.これはIllusieの問題を肯定的に解決するものである. Nearby cycleとは多様体の退化する族を考えるとき現れるもので,一般fiberのcohomologyを記述する特殊fiber上の層(の複体)である.これはDeligneによるWeil予想の証明の中の本質的な道具であった.semi-stableな退化に対してはRapoport-Zinkが明示的な計算を与えている. Kをhenselな離散付値体で剰余体kが分離閉なものとしXをその整数環OK上の有限型スキームとする.射i,jt, を次の図式で定義する. を次の図式で定義する. ここでKsはKの分離閉包,Kt=K( 1/m,p|m)⊂KtはKの最大tame分岐拡大,pはkの標数, 1/m,p|m)⊂KtはKの最大tame分岐拡大,pはkの標数, はKの素元である.このときnearby cycleの層 はKの素元である.このときnearby cycleの層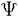 qおよびtame nearby cycleの層 qおよびtame nearby cycleの層 はそれぞれ はそれぞれ と定義される.nはpで割れない整数とする.I=Gal(Ks/K)をKの惰性群,P=Gal(Ks/Kt)をそのp-Sylow部分群とすると,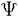 q, q, はそれぞれI,I/Pの自然な作用をもち, はそれぞれI,I/Pの自然な作用をもち, はP-不変部分( はP-不変部分(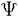 q)Pと一致する.Xがproperのとき,これらは次のスペクトル系列 q)Pと一致する.Xがproperのとき,これらは次のスペクトル系列 により,一般fiberのcohomology Hq(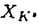 ,Z/nZ)を記述する. ,Z/nZ)を記述する. 本論文の主結果は,XがOK上log smoothとの仮定の下で,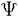 q= q= を示し,さらにそれを具体的に記述することである.XがOK上log smoothとは,Xがetale localにSpec OK[P]/( を示し,さらにそれを具体的に記述することである.XがOK上log smoothとは,Xがetale localにSpec OK[P]/( -x)と同型ということである.ここでPは有限生成な可換半群, -x)と同型ということである.ここでPは有限生成な可換半群, はOKの素元,x∈Pで次の条件を満たすものである. はOKの素元,x∈Pで次の条件を満たすものである. (1)PgpをPの群化とするときa∈Pgpがある整数m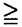 1に対しam∈Pを満たせばa∈Pである. 1に対しam∈Pを満たせばa∈Pである. (2)Pgp/XZのtorsion部分の位数はpと素である. (3)任意のa∈Pに対し,あるm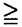 1とb∈Pがあって,P内でab=xmとなる. 1とb∈Pがあって,P内でab=xmとなる. 例えばsemi-stableなXはlog smoothであり,このときP=Nd= ,x= ,x= ととれる. ととれる. 主定理.XをOK上log smoothとすると, (1) (2)Xの各幾何的点yに対し,そこでのstalkは で与えられる. (2)の右辺の正確な定義は略すが,例えばX=Spec OK[P]/( -x)のときは, -x)のときは, で与えられる.この定理はIllusieの問題の肯定的解決を与えるものである. 主定理は通常のetale cohomologyについての主張であるが,それは次のlog etale cohomologyについての定理の帰結である. 定理.XをOK上log smoothとすると,X上のlog etale層(の複体)の標準射 は同型である.ここでj*は開うめこみj:XK→Xによるlog etale層の順像である. この定理は,通常のetale cohomologyにおけるsmooth acyclicityのlog版である.すなわち,log etale cohomologyを考えるにあたっては,log smooth射は通常のスキームの射としてはsmoothではないのに,smoothなものとみなしてよいことを意味している. 定理の証明はまずblow upにより,P=Ndの場合に帰着する.次に和:Nd→Nによるx∈Pの像に関する帰納法により,通常のetale cohomologyのsmooth acyclicityに帰着することによってなされる. 以上のように,中山氏は,本論文においてlog smoothの仮定の下,nearby cycleの層の計算を行いRapoport-Zinkの結果を拡張するとともに,Illusieの問題の肯定的解決を与えた.その証明においては,log etale cohomologyを有効に用い,それ固有の性質を示すとともに,それを用いることにより,通常のetale cohomologyの問題を見通しよく解決した.よって、論文提出者中山能力は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |