Mを有理係数ホモロジー球面、を結び目の自然な重複度,nをまつわり数とすると、Mの中の結び目S₁,S₂の絡み数は以下のように定義される。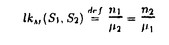

　このとき、Mをデーン・カービー表示することにより絡み数に関して以下の公式を得た。

　ここで,AはMのデーン・カービー表示をあらわす行列である。また、同時に以下のような結び目の傾きを求める公式も得た。sは結び目の傾きをあらわすものとすると以下がなりたつ。

　キャッソン不変量は絡み数のある種の和になっていることがキャッソンにより示されているが、同様なことがその拡張であるキャッソン・ウォーカー不変量についても成り立つことを示した。デーン・カービー表示されたMの中でK₊とK_-が以下のように正則表示されているとする。

　このとき、K₁とK₂を絡み目Lの成分とすると、Mが整数係数ホモロジー球面のときは、以下の式が成り立つ。

　ここで,’cはキャッソン不変量cの’である。これが,有理係数のときは以下のようになることを示した。

　ここで、dと〓はそれぞれ結び目のザイフェルト面の境界の成分数と傾きの分母をあらわす。この公式を用いれば、双曲的結び目や、その他、複雑な結び目などでデーン手術をほどこすことにより得られる有理係数ホモロジー球面のキャッソン・ウォーカー不変量も容易に求められる。

　整係数のホモロジー群が3次元球面S³と一致する3次元の閉じた多様体をホモロジー球面とよぶ.ホモロジー球面は,コンパクトな単連結4次元スピン多様体の境界になることが知られており,3次元トポロジーと4次元トポロジーを結び付ける重要な研究対象である.ホモロジー球面Mが与えられた時,Mを境界とする4次元スピン多様体の符号数は8で割り切れる.このを8で割った商が偶数か奇数かに応じて,Z₂の元の0または1を対応させたものが,ホモロジー球面MのRochlin不変量(M)である.1985年前後に,A.CassonはRochlin不変量を整数に持ち上げた新しい不変量_c(M)を定義した.Casson不変量はゲージ理論にも関係する深い不変量であることから多くの数学者によって研究された.

　さて、ホモロジー球面の拡張概念として,有理ホモロジー球面がある.これは有理係数のホモロジー群がS³と一致する3次元閉多様体である.有理ホモロジー球面Mについては1990年前後にK.WalkerによりCasson不変量を拡張するWalker不変量(M)が定義された.通常のホモロジー球面Mについては,

　$111437f07.gif$

　がなりたつ.

　論文提出者の藤田吾郎氏は,有理ホモロジー球面とその中の結び目理論について研究し,有理ホモロジー球面中の有理数値のまつわり数をその有理ホモロジー球面のKirby表示から計算する公式を与えた.さらに,まつわり数とWalker不変量との関係を明らかにした.この関係は通常のホモロジー球面の場合には,Cassonによって証明されたもので,藤田氏の関係式はこれを有理ホモロジー球面に拡張するものである.

　向きのついた有理ホモロジー球面Mが,S³の中の枠付き絡み目LによってKirby表示されており,Mの中のdisjointな2つの有向単純閉曲線C₁,C₂が,Lに交わらないS³の中の2つのループ(これも同じ記号C₁,C₂で表す)で表示されているものとする.Mが有理ホモロジー球面であることから,C₁とC₂の間には有理数値のまつわり数lk_M(C₁,C₂)が定義されるが,一般にはこの値の計算は容易でない.藤田氏の公式は,上のようにMがKirby表示されている状況のもとで,lk_M(C₁,C₂)の簡単な計算法を次のように与えるものである.

　$111437f08.gif$

　ここに,AはLのまつわり行列,rはC₁とC₂のS³の中での通常のまつわり数,A₁(あるいはA₂)はC₁(あるいはC₂)とLの各成分とのまつわり数を並べた横ベクトルである.S³の中のまつわり数は簡単に計算できるものであり,藤田氏の公式は有理ホモロジー球面中のまつわり数の計算を大幅に簡易化するものである.

　Kを,向きのついた有理ホモロジー球面Mの中の結び目とし,MからKの管状近傍の内部を除いた補空間をNとする.包含写像iから導かれた準同型i_*:H₁(∂N)→H₁(N)の核の生成元をとする.S³の中の結び目の場合には,がプリミテイブになるが,一般の有理ホモロジー球面の場合は,＝dyと書ける.ここに,dは自然数で,yはプリミテイブな1-サイクルである.境界∂N上の1-サイクルxを,xとyの交点数が1になるようにえらぶ.一般に,∂Nの1-サイクルaにS¹×D²の経線{*}×∂D²が一致するように,NにS¹×D²を張り付けてえられる有理ホモロジー球面をN(a)と表す:

　$111437f09.gif$

　このとき,kを任意の整数として,N(x+ky)とN(x)のWalker不変量の間には

　$111437f10.gif$

　の関係があることが知られているが,ここに現れた’^M(K)ははじめの有理ホモロジー球面Mの中の結び目Kの’Walker不変量’と考えられる.

　さて,Mの中の2つの結び目K₊とK_-とが一つの二重点のところで次のように関係しているとする.

　$111437f11.gif$

　藤田氏の第2の主定理は,’^M(K₊)と’^M(K_-)の差を,有理数値まつわり数によって記述するものである:

　$111437f12.gif$

　ここにK₁,K₂は絡み目Lの成分である.または,yがK方向に何回まわるかを表す整数である.

　この公式は,結び目KのDehn手術として得られる有理ホモロジー球面のWalker不変量の計算を,Kを上図の操作で簡単にして求めることを可能にする.藤田氏の有理数値まつわり数の計算公式と合わせれば,Walker不変量の計算はかなり容易になったということができる.論文の中で,これらの公式の証明は極めて巧妙になされている.

　以上の結果は3,4次元トポロジーの発展に寄与するところ大である.

　よって,論文提出者藤田吾郎氏は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認められる.