定電場の中にある量子力学的なN粒子系の運動を考える。結果を述べるために、記号の説明を加えながら進めていく。このような粒子系の運動は、total Hamiltonian  により支配される。但し、j粒子の質量、電荷、位置ベクトルをそれぞれmj,ej,rj∈Rdとし、Rd内の定電場を ≠0とし、 ≠0とし、 は、j粒子とk粒子との相互作用ポテンシャルVjkの和である。通常、散乱理論では、 は、j粒子とk粒子との相互作用ポテンシャルVjkの和である。通常、散乱理論では、 を重心座標系で考える。そのために、計量 を重心座標系で考える。そのために、計量 , , ∈RNd、配位空間 ∈RNd、配位空間 ,Xcm={r∈RNd|rj=rk for 1 ,Xcm={r∈RNd|rj=rk for 1 j<k j<k N}を導入する。また、正射影 N}を導入する。また、正射影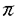 :RNd→X, :RNd→X,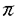 cm:RNd→Xcm,を用いて、x= cm:RNd→Xcm,を用いて、x=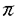 r,xcm= r,xcm=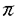 cmr, cmr, 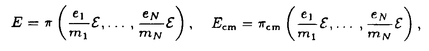 と書くことにする。このとき、 は、L2(RNd)=L2(X) は、L2(RNd)=L2(X) L2(Xcm)上、 L2(Xcm)上、 = = Id+Id Id+Id Tcmと分解され、そのうちHの方のみ考える。但し、 Tcmと分解され、そのうちHの方のみ考える。但し、   , , cmは、それぞれX,Xcm上のLaplace-Beltrami作用素である。E≠0のとき、Stark効果を持つといい、HをN体Stark Hamiltonianと呼び、その場合を考える。 cmは、それぞれX,Xcm上のLaplace-Beltrami作用素である。E≠0のとき、Stark効果を持つといい、HをN体Stark Hamiltonianと呼び、その場合を考える。 この論文での目的は、Schrodinger方程式id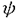 t/dt=H t/dt=H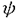 tの解 tの解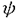 t=cxp(-itH) t=cxp(-itH)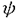 0の、t→±∞における漸近挙動を調べることにある。 0の、t→±∞における漸近挙動を調べることにある。 {1,…,N}の空でない部分集合(クラスター)による直和分解をクラスター分解と呼び、1クラスター分解(1,…,N)以外の全てのクラスター分解の集合を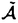 と表す。クラスター分解aがクラスター分解bの細分のとき、a⊂bと書く。 と表す。クラスター分解aがクラスター分解bの細分のとき、a⊂bと書く。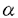 =(j,k)は、クラスター分解{(j,k),(1),…,( =(j,k)は、クラスター分解{(j,k),(1),…,( ),…,( ),…,( ),…,(N)}を表す。ここで、クラスター内部の運動を記述する配位空間Xa、クラスター間の相対運動を記述する配位空間Xaをそれぞれ ),…,(N)}を表す。ここで、クラスター内部の運動を記述する配位空間Xa、クラスター間の相対運動を記述する配位空間Xaをそれぞれ  と定義し、Xa,Xaの座標をそれぞれxa,xaで表し、 = = ,∂a= ,∂a= とする。簡単のため、 とする。簡単のため、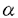 =(j,k)とし、 =(j,k)とし、 ( ( )=Vjk(rj-rk)と書く。subsystem Hamiltonian )=Vjk(rj-rk)と書く。subsystem Hamiltonian  、free Hamiltonian 、free Hamiltonian 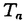 をそれぞれ をそれぞれ 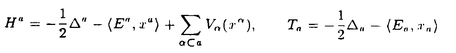 と定義し、L2(X)=L2(Xa) L2(Xa)上のcluster Hamiltonian Ha=Ha L2(Xa)上のcluster Hamiltonian Ha=Ha Id+Id Id+Id Taを定義する。但し、Ea,Eaは、それぞれEのXa,Xa成分、 Taを定義する。但し、Ea,Eaは、それぞれEのXa,Xa成分、 a, a, aは、それぞれXa,Xa上のLaplace-Beltrami作用素である。また、クラスター間の相互作用ポテンシャルをIa=H-Haで表し、 aは、それぞれXa,Xa上のLaplace-Beltrami作用素である。また、クラスター間の相互作用ポテンシャルをIa=H-Haで表し、 =Ia-Icと書く。 =Ia-Icと書く。 この論文での目的の一つは、考えている系に対する波動作用素の漸近完全性を示すことにある。ここで、波動作用素とは、  である。但し、Pa:L2(Xa)→L2(Xa)はHaの固有空間への正射影、Ua(t)はHaに対応するpropagatorで、short-rangeの場合にはexp(-itHa)を採る。漸近完全性とは、  のことである。但し、 (H)⊂L2(X)はHに関する連続部分空間である。これは、散乱状態 (H)⊂L2(X)はHに関する連続部分空間である。これは、散乱状態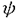 ∈ ∈ (H)の時間発展exp(-itH) (H)の時間発展exp(-itH)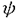 が、漸近的に が、漸近的に 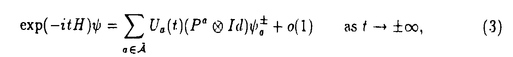  ∈L2(X),のように、各クラスターが束縛状態を形成しながら、クラスター同士は自由粒子であるかの如く振る舞う状態の重ね合わせで表せることと同値である。 ∈L2(X),のように、各クラスターが束縛状態を形成しながら、クラスター同士は自由粒子であるかの如く振る舞う状態の重ね合わせで表せることと同値である。 いま、質量と電荷との比が等しい粒子同士をまとめたクラスター分解をcで表す。ポテンシャルの仮定を、次のように置く。  は実数値関数で、 は実数値関数で、  を、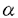 ⊂cのときには ⊂cのときには -1<p -1<p 1、 1、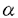 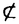 cのときには0< cのときには0<  1/2、に対して満足している、 1/2、に対して満足している、 または、  は実数値関数で、 は実数値関数で、  を、ある -1< -1<  1に対して満足している。 1に対して満足している。 ここで、 ⊂cのとき、j粒子とk粒子の質量と電荷との比は等しく、 ⊂cのとき、j粒子とk粒子の質量と電荷との比は等しく、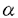 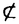 cのとき、j粒子とk粒子の質量と電荷との比は異なることに注意する。上の条件を満足しているならば、ポテンシャルはlong-rangeであるという。まず、(V)Gを仮定し、a⊂cなるクラスター分解のみ考える。このとき、aのクラスター内の粒子同士では、質量と電荷との比が等しいことに注意しておく。いま、Graf型波動作用素 cのとき、j粒子とk粒子の質量と電荷との比は異なることに注意する。上の条件を満足しているならば、ポテンシャルはlong-rangeであるという。まず、(V)Gを仮定し、a⊂cなるクラスター分解のみ考える。このとき、aのクラスター内の粒子同士では、質量と電荷との比が等しいことに注意しておく。いま、Graf型波動作用素 を を  で定義する。但し、Da= とする。このとき、次の結果が主要な結果の一つである。 とする。このとき、次の結果が主要な結果の一つである。 定理1.1.1.(V)Gを仮定する。このとき、Graf型波動作用素 ,a⊂c,が存在し、それらは漸近全である、つまり、 ,a⊂c,が存在し、それらは漸近全である、つまり、  次に、(V)Dを仮定する。このとき、Dollard型波動作用素を  で定義する。但し、Da,⊥=Da-E〈E,Da〉/|E|2は、Daの、Eに直交する成分である。このとき、次の結果がもう一つの主要な結果である。 定理1.1.2.(V)Dを仮定する。このとき、Dollard型波動作用素 ,a⊂c,が存在し、それらは漸近完全である、つまり、 ,a⊂c,が存在し、それらは漸近完全である、つまり、  上の二つの定理を示すのには、 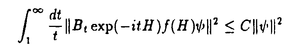 という形の積分評価で与えられた伝播評価が、非常に重要な役割を果たしてきた。但し、Btは、時刻tに依存する有界な擬微分作用素、あるいは、より一般的な作用素であり、f∈ (R)とする。これに対して、時刻tについての各点評価 (R)とする。これに対して、時刻tについての各点評価  なるものも、定電場がない場合には、Skibsted氏等により研究されているが、定電場のある場合には、まだ研究されていないようである。そこで、この論文の後半では、各点評価の形の伝播評価を、N体のStark Hamiltonianに対して導出している。ここで得られた評価は、オブザーバブルDとxが、t→∞のときに、ほぼD-Et=o(t)とx-Et2/2=o(t2)のように振る舞うことを示したものであり、これまでの積分評価よりもシャープな結果も得られている。より精密に結果を述べるために、次のようなポテンシャルの仮定を置く。  は実数値関数で、 は実数値関数で、  を満たす。 このとき、次の結果を得る。 定理2.1.1.Vが(V.1)と、(V.2)または(V.3)を満たしているとする。 >0,s>s’>0とする。このとき、次の評価がt >0,s>s’>0とする。このとき、次の評価がt 1に対して成立する。 1に対して成立する。  この結果は、時間発展に従って、|D-Et|=o(t),|x-Et2/2|=o(t2)となることを示している。次の定理は、上の性質の精密化である。特に、(V.2)を0<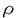  1/2で仮定すると、クラスター間の相対運動(xc,Dc)と全運動(x,D)の、tについての増大度には差異が生じ得ることを示している。 1/2で仮定すると、クラスター間の相対運動(xc,Dc)と全運動(x,D)の、tについての増大度には差異が生じ得ることを示している。 定理2.1.2.Vが(V.1)と、(V.2)または(V.3)を満たしているとする。(V.2)が0<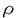 <1/2で満たされているならば、 <1/2で満たされているならば、 とし、(V.2)が とし、(V.2)が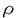 =1/2で満たされているならば、s0( =1/2で満たされているならば、s0(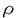 )=1, )=1,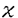 1(t)=(logt)1/2, 1(t)=(logt)1/2,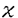 2(t)=t(logt)1/2とし、(V.2)が 2(t)=t(logt)1/2とし、(V.2)が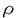 >1/2で、あるいは、(V.3)が満たされているならば、s0( >1/2で、あるいは、(V.3)が満たされているならば、s0(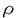 )=1, )=1,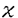 1(t)=1, 1(t)=1,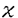 2(t)=tとする。 2(t)=tとする。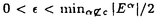 とする。このとき、次の評価がt とする。このとき、次の評価がt 1に対して成立する。 1に対して成立する。  更に、Vが(V.1)と(V.2)を0<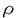  1/2で満たしているならば、クラスター間の相対速度Dcと相対位置xcは、次の評価をt 1/2で満たしているならば、クラスター間の相対速度Dcと相対位置xcは、次の評価をt 1に対して満たす。 1に対して満たす。  系2.1.3.Vが(V.1)と(V.2)を、0<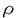  1/2で満たしているとする。s0( 1/2で満たしているとする。s0(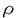 ), ),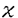 1(t),x2(t)は、定理2.1.2と同じとする。 1(t),x2(t)は、定理2.1.2と同じとする。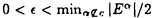 ,0< ,0< <s0( <s0(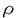 )とする。このとき、次の評価がC>0,t )とする。このとき、次の評価がC>0,t 1に対して成立する。 1に対して成立する。  次に、cがNクラスター分解である場合を考える。次の定理は、Dt-Et2/2の方がEt2/2よりも、xの良い近似であることを示している。 定理2.1.4.Vが(V.1)と、(V.2)または(V.3)を満たしているとする。s0( ), ), 1(t)は、定理2.1.2と同じとする。このとき、次の評価が任意のmulti-index 1(t)は、定理2.1.2と同じとする。このとき、次の評価が任意のmulti-index ,s>2| ,s>2| |s0( |s0( ),t ),t 1に対して成立する。 1に対して成立する。  特に、定理2.1.2の最初の二つの評価が、波動作用素の漸近完全性を示すのに利用できることに注意しておく。 |