状態量に不等式拘束条件を有する最適制御問題の数値解法に関する一提案を行った。従来、最適制御問題における状態量不等式拘束の取り扱いには、様々な工夫がされてきた。状態量不等式拘束の定式上の取り扱いは、直接法と間接法の二つに大別される。直接法と言うのは、解を拘束にかかる部分(アーク)とかからない部分とに事前に分け、前者に対してのみ拘束条件を等式拘束として課す手法である。この場合、拘束にかかり始める時間や離れる時間を変数として定式化し、拘束中においてのみ、これを直接満たす様に制御量を計算するために、精度が高いと言われているが、拘束にかかる入り口点がすべて内部境界点となるため、多点境界値問題を形成することとなる。従って当然のことながら、計算を始める前にアークの数や順序が既知であることが必要となる。これに対して、解全体を一つのアークとして考える手法が、間接法と総称される。間接法には色々なタイプの物が提案されているが、これらは拘束中の制御量を拘束条件から直接算出するか否かで大きく二つに分類できる。前者は、いわゆるペナルティ法として知られる。後者は、何らかの変換法を用いて、不等式拘束を、制御量を直接算出可能な条件式に置き換えて用いる手法である。これには、Martensson のConstraining Hyperplane法、Jacobsonらのスラック変数法、高野らの単調区間法等があげられる。 工学的応用の観点からは、事前に最適解の形状について情報を必要とせず、拘束上ではこれを順守する様な制御量が直接得られるタイプの間接型定式化が望ましいと言える。こうした定式化のうち、数学的な厳密性と数値的な微分可能性を合わせ持った手法となると等式拘束変換法(スラック変数法)に基づく定式化が唯一であり、その意味で極めて有用な手法と言える。 しかし、この手法には古くから利用されている変分法に基づく数値解法の内、より収束特性に優れた二次の解法が適用できないという欠点が指摘されてきた。 本研究では、等式拘束変換法(スラック変数法)に基づく定式化にも適用可能な改良型の二次解法として、従来の一次解法と二次解法を結合したハイブリッド型の準二次解法を提案した。 今、スラック変数法を用いて状態量不等式拘束条件を状態量/制御量混合型等式拘束条件S=0に変換したとする。すなわち、問題をベクトル量  に対して、評価関数を最小化する問題とし、その時のハミルトニアンをH、微分方程式に対するアジョイントを とする。この時、従来の二次解法では、制御量、等式拘束条件式のアジョイントの更新量 とする。この時、従来の二次解法では、制御量、等式拘束条件式のアジョイントの更新量 u、 u、 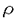 を を 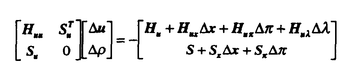 なる式から算出する。スラック変数法に基づく定式化ではこの左辺のマトリクスが拘束上で特異となるため二次解法が使えないとされてきた訳である。本論文では、これを回避すべく対角行列 を設定して を設定して  より制御量、等式拘束条件のアジョイントの更新量を求める。 の設定に関しては、前述のマトリクスの特異性の他、解法の最適解への接近特性や、解の安定性等様々な勘案すべき要素が存在するが、簡単な設定方法としては、スラック変数法によって導入されたダミー制御量に対する項に対してのみ の設定に関しては、前述のマトリクスの特異性の他、解法の最適解への接近特性や、解の安定性等様々な勘案すべき要素が存在するが、簡単な設定方法としては、スラック変数法によって導入されたダミー制御量に対する項に対してのみ の要素を1に設定する方法が考えられる。 の要素を1に設定する方法が考えられる。 本論文では、こうした設定の元で、古来から変分法の問題として名高い最速降下線問題で途中に不可侵領域がある場合(図1、2)を数値計算例として取り上げ、新解法の優れた特性を確認した。表1、2は新解法と従来の一次解法による数値計算の様子である。これから、同じ収束条件(ここでは最適性条件のエラーQ<1.5×10-3)で計算した場合、新解法ではわずかに10回程度の繰り返し回数で収束しているのに対し、従来の一次解法ではその3倍近い計算回数が必要となっているのが見て取れる。また、拘束条件のエラーPに関しては、新解法の方がこの時点で一桁以上すぐれた達成状況にあることもわかる。(図3に示す様にどちらの解法も同じ収束解に到達している)これから、新解法は二次解法の特性を十分そなえた上で、スラック変数法を用いた問題にも適用できる解法であることが確認できた。  図表図1 例題の概念図 / 図2 例題の拘束条件 図表図1 例題の概念図 / 図2 例題の拘束条件 図3 例題の収束解 図3 例題の収束解 図表表1 新解法による例題の計算結果 / 表2 一次解法(CGRA法)による例題の計算結果 図表表1 新解法による例題の計算結果 / 表2 一次解法(CGRA法)による例題の計算結果 さらに、実際的な応用例として空気吸い込み型エンジン(Air Turbo Ramjet)を用いた高速実験機の飛行経路の最適化に同手法を用い、最適飛行経路を得た(図4)。図中最適解と共に記された二曲線は初期解である。この問題では、  が実験目的から決まっている。また、ATRエンジンの作動域から、その飛行動圧に制限があり、これが状態量不等式拘束となっている。  これらの条件のもとで、実験機をできるだけ小規模に抑さえるために、  を目指す。ここでは、エンジンサイズも最適化されるパラメータとなっている。得られた最適経路は、簡単な指標である実効比推力  (図5)から予想される結果にほぼ一致している。即ち、最も実効比推力が小さくなって飛行条件が厳しい音速付近を小さめのエンジンで越えるため、この付近では、旦上昇した後わずかに降下する。そこからあとは、高動圧側が実効比推力が大きくなるため、ほぼ50kpaの制限動圧に沿って飛行する場合となっている。 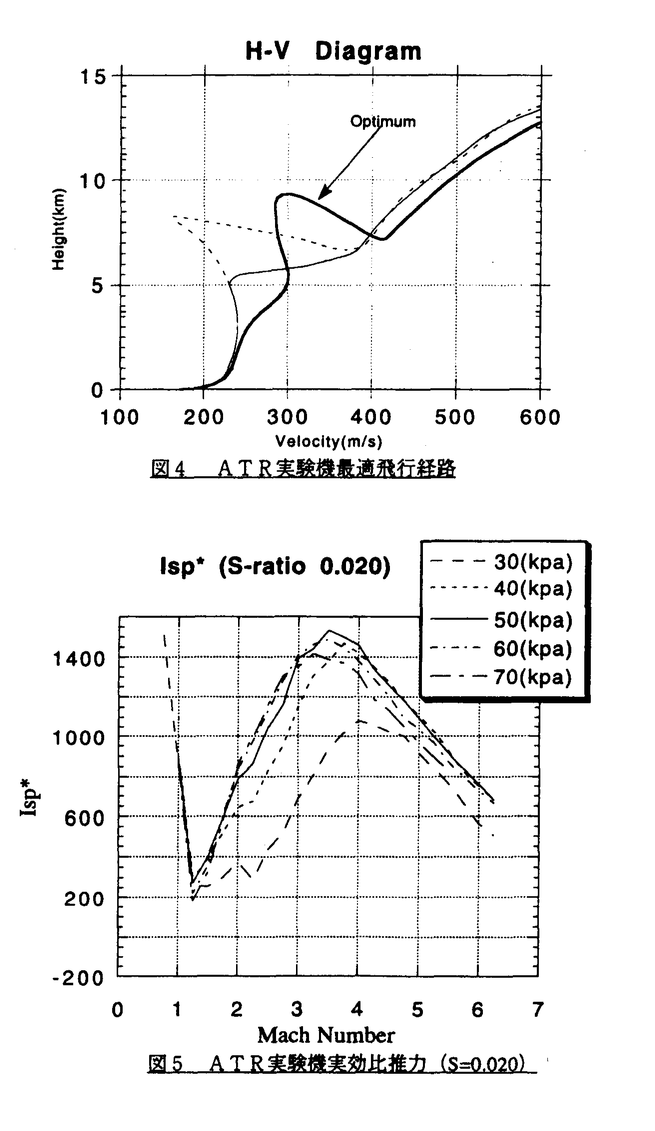 図表図4 ATR実験機最適飛行経路 / 図5 ATR実験機実効比推力(S=0.020) 図表図4 ATR実験機最適飛行経路 / 図5 ATR実験機実効比推力(S=0.020) 以上の様に、本論文では、等式拘束変換法(スラック変数法)に基づく定式化にも適用可能な改良型の二次解法として、従来の一次解法と二次解法を結合した準二次解法を提案し、典型的な数値計算例を用いてその特長を明らかにした。 さらに、実際的な応用例として空気吸い込み型エンジンを用いた高速実験機の飛行経路の最適化に同手法を用い、その実用性が確認できたといえる。 |