シュレディンガー方程式に従う量子系の電磁場中での振る舞いを理解するのには、二準位系と単一輻射場の単純なモデルが広く用いられている。また、実際には多準位系多輻射場のケースでも、いくつかの独立した二準位系が組み合わさったとして解析を行うことが多い。例えば図1(a)のような二つの輻射場を含む二重共鳴実験の場合を考える。この系の励起準位からの蛍光量、つまり励起状態のpopulationは、二つの二準位系(基底状態間、および励起状態と基底状態の間)がともに共鳴状態になったとき最大になるというわかりやすい理解が可能である。この場合、片方の輻射場の周波数を固定しもう一方の周波数を掃引すると、シングルピークのスペクトルが得られると期待される。しかし、図1(a)のさらに細かい準位構造(ゼーマン副準位)と選択則を考慮すると、この系は図1(b)のような9準位8輻射場の問題になる。(ここで幅射場には適当な偏光を仮定した。)果たしてこの系の蛍光スペクトルはどのようなものになるだろうか。図1(b)においてRF場の周波数を固定し、レーザー光の周波数を掃引したときの蛍光スペクトルを数値的に求めたのが図2である。(この図は単純に多準位の光学的Bloch方程式の定常解を解くことで得られ、特殊なものでは全くない。)スペクトルの概観は確かに期待されたシングルピークだが、共鳴点付近で複雑な構造が存在しているのがわかる。本研究の最も有効な結果の一つは、任意の多輻射場中の任意の多準位系原子の持つこのスペクトル構造の解析的な予測が初めて可能になったということである。 蛍光スペクトルは、本質的に輻射場によるPumpingと自然放出によるDecayの釣り合いによって決まる量であり、緩和過程を無視した計算から得られることは無い。この緩和項の存在はBloch方程式の対称性を崩すため、任意の多準位系の一般的な理論を展開することは難しい。例えば、3準位+2輻射場系の蛍光スペクトルの(長大な)解析解すら1975年になって初めて得られた[1]。また、これまでの一般論としては、電場強度と離調周波数に特殊な条件を課したものだけが存在している。しかしこれらの理論は、例えば図2を説明することすらできない。 さて、図2に見られるDipはDark Resonance(もしくはAnti-resonance,Inverse-Raman resonance,Trapped state,Population trapping等)と呼ばれる多光子過程であることが本研究により明らかになった。Dark Resonance(以下DR)そのものはA型の3準位+2輻射場系で初めてあらわれる現象であり、文献1の解析解を用いてBrewerらによって説明された[2]。DRは自然幅よりもさらに狭い共鳴線幅を持っていて、応用は高精度分光に留まらず、自然放出による反跳限界以下の原子トラップ等に広く利用されている。面白いことに、この現象は2準位、V型あるいはカスケード3準位では起こらない。本研究ではエネルギー準位+輻射場のconfiguration(ネットワーク図)とDRが生じるかどうかの関係、及びそのときの暗線の本数の関係を定式化した。例えば図1(b)では15本の暗線が図3の位置に現れることが解析的な計算で示され、density matrixのHamiltonian行列が81×81の大きさを持つこの系の数値計算を行う必要は無くなった。また本研究によると、数値計算では解りにくいスペクトルの微細構造を明らかにすることができる。図3の数値解からは5ないしは7本の暗線構造しか判らないが、実はそこには15本の微細構造が存在していた。このように、1光子近似を用いたシングルビークの輝線構造と、本研究により得られる多光子過程の暗線構造を合わせることで、任意多準位系の呈する図2のようなline shapeはただちに予測が可能となった[3]。  図1 図1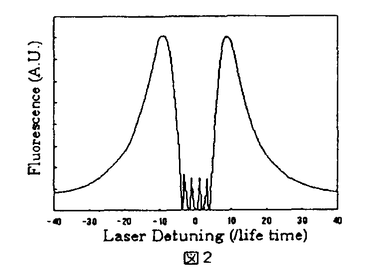 図2 図2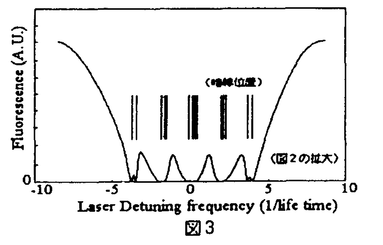 図3 図3 また、DRはもともと中性原子のレーザー冷却の極限温度を決める現象として注目を集めていた。本研究はDRの現れる周波数を解析的な形で提供するため、冷却原子の幅射場によるマニュピレーション、高精度衝突実験を行なう際の最も基礎的な理論面での予測を与えるものである。 次に、実際にDRを実験に応用する場合、DRの共鳴幅を決める要素及びそのtransientな振る舞い等を調べる必要がある。Brewerらの報告[1]以降、3準位以上のline profileの完全な(つまり全てのパラメータを含んだ)解析は行われていなかったが、本研究では5準位系+4輻射場の系の完全な(非常に長い)解析解を初めて得た[4]。特に5準位系は中性原子トラップ実験への応用が有望でしかも実験的に得やすい系(核スピンI=3/2を持つアルカリ原子)であり、現在我々の研究室で進められている4準位系の解析に先駆けて行われた。そしてDRの共鳴幅が解析的な形で求められ、3準位系でのDRに比べて5準位系のDRは、その共鳴幅が次の比で狭いということがわかった。(ここで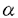 、 、 はレーザー光及びRF場の共鳴ラビ周波数) はレーザー光及びRF場の共鳴ラビ周波数) 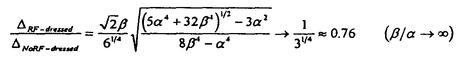 これは物理的には、暗共鳴状態への"遷移"強度が、暗線の分裂によって小さくなるためと考えられている。この、強い輻射場中でも共鳴幅が狭く保たれる性質は、トラップ実験などへの応用に特に役立つと思われる。また、系のtransientな振る舞いを数値計算により求め、DRの収束時間はその共鳴幅の逆数によって決まることも確かめられた。 最後に、DRの新しいブランチの実験的な観測を初めて行った[5]。図4がその実験図である。前述の5準位系をK39により得た。対称な形を持つ5準位系の特殊性(ドップラーシフトしないDR位置)から、光と原子ビームを平行に照射してもDRが検出できるため、観測に必要な長い相互作用時間を確保することができ、通常の観測に必要な原子トラップやレーザークーリングを用いなくともよかった。また5準位系のline profileの解析解から得られた、DR検出のための相互作用時間の下限、レーザーの線幅の下限、およびRFパワーの(criticalな)許容範囲を求め、注意深く実験を行った。図5がその実験結果であり、RFパワーの見積もり誤差を考慮すると前出のDR位置の理論的予測とほぼ一致した。 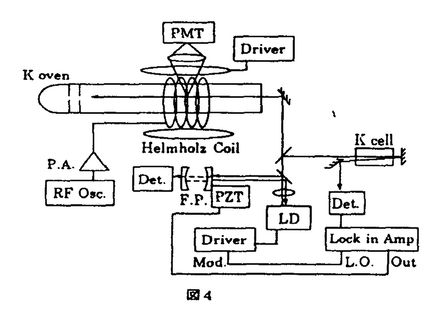 図4 図4 図5 図5 実験で検出されたDRのディップの浅さは、主として相互作用時間の不足にあると考えている。そのため、研究の次の段階として、カリウム原子を用いたレーザークーリングを実現し[6]、DR実験やトラップ実験への応用を考えている。半導本レーザー光にRF周波数変調をかけ、そのサイドバンド光をリポンプ光に用いることで、比較的簡単にカリウム原子のレーザークーリングを行うことができた。実験結果から、0m/sおよび320m/sの速度分布に大きなピークを作ることができた。この技術により、ms程度の相互作用時間を得ることが期待でき、DR実験への応用が期待される。 [1] R.G.Brewer and E.L.Hahn Phys.Rev.A 11 1641(1975) [2] E.Arimondo and G.Orriols Lett.Nuovo Cimento 17 333(1976) [3] H.Kanokogi and K.Sakurai submitted to Phys.Rev.A [4] H.Kanokogi and K.Sakurai in press on Phys.Rev.A(Mar.1996) [5] H.Kanokogi and K.Sakurai in preparation [6] H.Kanokogi,H.Numata,T.Mitsui and K.Sakurai not published |