学位論文要旨
| No | 111654 | |
| 著者(漢字) | 秦泉寺,雅夫 | |
| 著者(英字) | ||
| 著者(カナ) | ジンゼンジ,マサオ | |
| 標題(和) | 位相的シグマ模型への幾何学的アプローチ | |
| 標題(洋) | Geometrical Approach to Topological Sigma Model | |
| 報告番号 | 111654 | |
| 報告番号 | 甲11654 | |
| 学位授与日 | 1996.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(理学) | |
| 学位記番号 | 博理第3018号 | |
| 研究科 | 理学系研究科 | |
| 専攻 | 物理学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 近年,位相的場の理論は,具体的に解ける模型として飛躍的な発展を遂げている。この論文は特に位相的シグマ模型についてその発展の成果を踏まえつつ独自の展開を行った物である. 位相的シグマ模型はN=2超対称性を持つシグマ模型をtwistして得られる位相的場の理論でありリーマン面 特に,Mが複素3次元カラビ-ヤオ多様体の場合,Mのミラー多様体M*が存在してM上のA-模型とM*上のB-模型とが同型であり,M*上のB-模型を解いた結果をM上のA-模型の結果に翻訳することによりM上のA-模型を解くことができることが提唱されてきた.(ミラー仮説)実際その仮説に基いて計算された結果の一部は代数幾何を用いて計算されたA-模型の結果に一致し,その仮説の正当性が謳われてきた. 当初,カラビ-ヤオ多様体Mに対してそのミラー多様体M*を見つけることはある程度実験的な手法に頼っていたが,Batyrevらによってそれらはカラビ-ヤオ多様体を埋め込むトーリック多様体の間の双対性に帰着されることが示された.この構成法は複素3次元のカラビ-ヤオ多様体に限らず容易に一般次元のカラビ-ヤオ多様体に拡張出来るものであった. 筆者はこれに着目して名倉氏と共同でCPN-1に埋め込まれたカラビ-ヤオ多様体MN上のA-模型を取り扱い,一般次元のミラー仮説を仮定してそのミラー多様体 この仕事を行った年には,数学者達により重力が結合した形でのA-模型の研究に大きな進展が見られた.特にKontsevich,Manin,Dubrovinらにより,MがFano多様体の場合(c1(KM)が正でカラビ-ヤオ多様体より大きく曲がった多様体),オペレーターの間に定義される代数の結合律を仮定して得られる等式(DWVV方程式)を用いて解けることが示された.この結果を利用して筆者は孫氏と共同でMがCP3,CP4及びGr(2,4)の場合に重力が結合した形でのA-模型の相関関数を求めた. またKontsevichによりCP4に埋め込まれたカラビ-ヤオ多様体内の代数曲線(上記の正則写像に当たる)の数え上げが,重力が結合した場合の正則写像のモジュライ空間を正確に記述する安定写像の概念とBottの留数公式を組み合わせることで任意次数の正則写像に対して可能であることが示された(この方法をtorus action法と呼ぶことにする). 筆者はこの方法が重力が結合した形でのMN上のA-模型を解くことに応用できる事を発見し、この模型の相関関数の生成関数の積分表示を得た.更に3点関数が重力の有無に依らないことと,純粋なA-模型に対して成り立つfusion rule(これを用いると任意の相関関数を3点関数の積の和で書ける)を組み合わせてミラー仮説からの結果を純粋にA-模型の立場から導き出し,MNの場合の一般次元のミラー仮説の正当性を完全に示した. 次に筆者は、上記の方法で得た相関関数の生成関数の積分表示をCPN-1内のk次超曲面 本論文は、以上の仕事をまとめたものである.論文内では幾何学的色彩の濃い順に並べてある. 第一章は導入章であり,位相的場の理論の歴史及び論文の内容を時間的順序に従って概観する. 第二章では位相的シグマ模型(A-模型)を解説し,相関関数が複素球面からケーラー多様体Mへの正則写像のモジュライ空間の交点数である事,更にそれがオペレーターから課される条件を満たす正則写像の個数として与えられる事を導く。次にMがCPN-1内のk次超曲面 第三章では上記の公式を用いて相関関数を幾何学的に評価する.まず複素球面からCPN-1への多項式写像の考えを用いて相関関数を荒らく評価する.又この評価の限界についても議論する.次に次数1の正則写像の場合にグラスマン多様体Gr(2,N)のコホモロジー環の理論を用いて相関関数のある系列を厳密に計算する.以降は重力が結合した場合のモジュライ空間の解説で,まず導入として頂点つき複素球面のモジュライ空間(安定曲線)の理論を解説する.次にそれを利用した安定写像の定義を紹介する,最後にtorus action法を導入し, 第四章はオペレーター代数に関連した話題を取り扱う.まず,前章の結果を利用して 第五章は,ミラー対称性を取り上げる.まずBatyrevの構成法を用いてMNのミラー多様体 | |
| 審査要旨 | 自然界の全ての力を統一する理論の最有力候補として精力的に研究されている超弦理論において最も重要な課題の一つは、10次元で定義されるこの理論からどのようにして物理的な4次元時空での理論を構築するかといういわゆる時空のコンパクト化の問題である。これについては、4次元理論として現象論的に有望なN=1の超対称性を実現するためには、内部空間が6次元(複素3次元)のリッチ平坦なケーラー多様体、いわゆるカラビ・ヤウ多様体、でなければならないということが良く知られている。さらに、幾つかの物理的に重要な量、例えば湯川結合や世代数、がこの内部空間の位相幾何学的性質で決定されることもわかっている。従ってカラビ・ヤウ多様体上の弦理論の研究は超弦理論の深い理解にとって非常に重要である。カラビ・ヤウ多様体上の弦理論はN=2の超対称シグマ模型で記述されるが、その位相的性質は、このモデルに現れる場のスピンをシフト(twistという)して得られる「位相的シグマ模型」で記述されることがWittenによって示された。このtwistの仕方は本質的に2通りあり、得られる模型は、A-模型、及びB-模型と呼ばれる。A-模型はリーマン面 本論文はこうした発展を背景に、複素3次元という制約を越えて、一般次元のあるクラスのケーラー多様体に対するA-模型を解析し、その相関関数を代数幾何学的手法を開発することによって計算することに成功した。さらに、多様体が一般次元のカラビ・ヤウ多様体の場合には、結果はミラー多様体上のB-模型での計算結果と完全に一致し、従ってミラー対称性が高次元にも拡張できることを初めて示した。 第1章では位相的場の理論の発展の状況と本論文の結果のまとめが述べられている。 第2章ではA-模型についての解説を行った後、多様体が一般次元(N-1)複素射影空間CPN-1内のk次超曲面 第3章がこの論文の主要部分であり、ここでは前章で導いた積分公式を代数幾何学的な手法を開発して具体的に評価している。とくに写像の次数が1の場合にはグラスマン多様体Gr(2,N)のコホモロジー環の理論を用いて相関関数を厳密に計算することに成功している。さらに2次元重力と結合した場合の計算も行っている。 第4章では前章の結果を利用して、物理量のオペレーター代数を計算し、幾つかの具体的な模型を解いている。 最終章の第5章では、一般次元のCPN-1中で実現できるカラビ・ヤウ多様体の場合に、前章まででA-模型を直接扱って得られた結果が、ミラー多様体上のB-模型での計算結果と厳密に一致することからミラー仮説が高次元にまで拡張可能であることを示している。 以上述べたように、本論文は超弦理論の重要な問題に関して、高度な数理物理的手法を開発駆使して興味深い新しい知見を得たものであり、高く評価される。よって審査員一同博士(理学)の学位を与えるに十分なものと判断した。尚、本論文の一部は共同研究に基づくが、その部分に関しても論文提出者が十分な寄与をしたことを確認した。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/53900 |
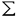 からケーラー多様体Mへの写像を記述する.一般のケーラー多様体Mの場合にはA-twistと呼ばれるtwistのしかたが許され,この場合をA-模型と呼ぶ.特にMがカラビ-ヤオ多様体の場合はB-twistと呼ばれるtwistの仕方も許されこの場合をB-模型と呼ぶ.A-模型はリーマン面
からケーラー多様体Mへの写像を記述する.一般のケーラー多様体Mの場合にはA-twistと呼ばれるtwistのしかたが許され,この場合をA-模型と呼ぶ.特にMがカラビ-ヤオ多様体の場合はB-twistと呼ばれるtwistの仕方も許されこの場合をB-模型と呼ぶ.A-模型はリーマン面 のB-模型の結果からMN上のA-模型の相関関数の一系列を求めた.この相関関数は,前述のとおりリーマン面(今の場合は複素球面)からMNへの正則写像のモジュライ空間の交点数(もっと具体的には観測オペレーターから課される条件を満たす正則写像の個数)としての意味を持つ筈のものであった.そこで具体的にA-模型の立場から交点数を評価する事を筆者は試みた.まず上記のモジュライ空間が複素球面からCPN-1への正則写像のモジュライ空間の部分空間として実現出来ることと複素球面からCPN-1への正則写像が多項式写像の形で書ける事を用いて相関関数の次数dの正則写像の寄与がNdN+1と評価出来ることを示した.実際この結果はミラー仮説からの結果のN-展開の主要部を再現しておりこのアプローチが基本的に正しいことを示している.またさらに次数1の正則写像の複素球面からCPN-1へのモジュライ空間がグラスマン多様体Gr(2,N)を用いて厳密に表現出来ることを用いて次数1の寄与を代数幾何的手法を用いて厳密に再現した.これによりある程度一般次元のミラー仮説の正当性を示したことになる.
のB-模型の結果からMN上のA-模型の相関関数の一系列を求めた.この相関関数は,前述のとおりリーマン面(今の場合は複素球面)からMNへの正則写像のモジュライ空間の交点数(もっと具体的には観測オペレーターから課される条件を満たす正則写像の個数)としての意味を持つ筈のものであった.そこで具体的にA-模型の立場から交点数を評価する事を筆者は試みた.まず上記のモジュライ空間が複素球面からCPN-1への正則写像のモジュライ空間の部分空間として実現出来ることと複素球面からCPN-1への正則写像が多項式写像の形で書ける事を用いて相関関数の次数dの正則写像の寄与がNdN+1と評価出来ることを示した.実際この結果はミラー仮説からの結果のN-展開の主要部を再現しておりこのアプローチが基本的に正しいことを示している.またさらに次数1の正則写像の複素球面からCPN-1へのモジュライ空間がグラスマン多様体Gr(2,N)を用いて厳密に表現出来ることを用いて次数1の寄与を代数幾何的手法を用いて厳密に再現した.これによりある程度一般次元のミラー仮説の正当性を示したことになる. 上の重力が結合したA-模型の場合に拡張した.(MNは今の場合
上の重力が結合したA-模型の場合に拡張した.(MNは今の場合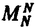 に当たる.)これを用いてこの模型の3点関数を計算しMNの場合と同様の論理で
に当たる.)これを用いてこの模型の3点関数を計算しMNの場合と同様の論理で