学位論文要旨
| No | 111655 | |
| 著者(漢字) | 藤堂,眞治 | |
| 著者(英字) | ||
| 著者(カナ) | トウドウ,シンジ | |
| 標題(和) | ハードコア系の固相液相転移と臨界現象 | |
| 標題(洋) | Solid-Fluid Phase Transitions and Critical Phenomena of Hard-Core Systems | |
| 報告番号 | 111655 | |
| 報告番号 | 甲11655 | |
| 学位授与日 | 1996.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(理学) | |
| 学位記番号 | 博理第3019号 | |
| 研究科 | 理学系研究科 | |
| 専攻 | 物理学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 物質の三態(気相、液相、固相)、およびそれらの間の相転移は統計力学における最も基本的な問題の一つとして、非常に長い研究の歴史をもっている。これらの相転移は一般には一次転移であるが、気相と液相との共存線がある湿度(臨界温度)で消えてしまい、それ以上の温度では気相と液相とは区別できなくなってしまうのに対して、固相と液相との共存線は高温においても消えることはない。この事実は、固相と液相(もしくは気相)との間には本質的な対称性の違いがあることを示している。一般に単純な気体のもつ相互作用ポテンシャルは、無限の斥力をもつ剛体芯(ハードコア)の部分と有限の引力の部分とから成り立っていると考えられるが、高温の極限では有限の引力の部分は無限の斥力ポテンシャルに比べ無視することができる。したがって、固相液相転移は本質的にはハードコアポテンシャルのみで記述できると期待される。実際、1962年にAlderとWainwrightは分子動力学法を用いて、二次元のハードコアのみをもつ粒子系における一次転移(いわゆるAlder転移)の存在を数値的に明らかにした。それ以来、理論的、また数値的に精力的に研究が行われてきたが、その本質的なメカニズムは依然不明瞭である。 このハードコア系の固相液相転移の問題について、第二章、三章では離散空間上で定義された気体(格子気体)を議論する。この模型は一次転移だけではなく、さまざまな二次転移も示す興味深い系である。一方、第四章ではビリアル展開を用いた、はじめから連続空間上、かつ熱力学的極限での議論を行う。 第二章では、二次元古典格子気体を転送行列の方法、および現象論的繰り込み群、共形不変性などを用いて議論する。自明でない相転移を示すもっとも単純な模型は最近接排除ポテンシャルをもつ格子気体であるが、この模型の相転移は厳密解、転送行列法をはじめとして、さまざまな方法を用いて調べられている。一方、次近接相互作用まで考えると、転送行列法では行列の次元の大幅な増大という困難のため、計算機上で扱える系の大きさは最近接相互作用のみの場合に比べかなり制限される。大規模行列を取り扱う場合、標準的なテクニックとして「疎行列分解」という方法がしばしば用いられる。転送行列は一般に「密な」行列であるが、それをO(N)個の「疎な」行列の積に分解することにより、計算時間および必要なメモリ容量を大幅に減らすことができる。また一方で、排除ポテンシャルが存在する場合には、転送行列の要素のうちかなりの数が恒等的に零となるため、行列の次元は実質的に大幅に減らすことが可能となる。 これらの方法は両者それぞれ、ハードコアポテンシャルをもつ格子気体に適用され、成功をおさめてきた。例えば、最近接排除ポテンシャルのみをもつ格子気体の場合、密な転送行列をそのまま扱った場合には、現在の計算機では最大でN=13の系しか扱えないが、上記の方法を用いればそれぞれN=24および19の系まで扱うことが可能となる。しかし、残念ながら、一般にはこれらの方法は両立しない。本論文では、後者の方法で減らした行列の次元を、再び少しだけ増やすことによって、転送行列を「次元の小さな疎行列」に分解する方法を提案する。この方法については付録で詳しく議論をする。この新しい方法を用いることによって、上記の例では最大N=35の系まで扱うことが可能となる。また、次近接相互作用をもつ系にも拡張することができ、従来の方法に比べかなり大きな系の計算が可能となった。 第二章では、上記の方法を用いて、最近接排除ポテンシャルおよび次近接相互作用をもつ二次元格子気体の相転移とその臨界現象を調べ、詳しい相図を得た。最近接排除ポテンシャルのみをもつ系は二次の転移を起こすことが知られている。正方格子および三角格子上では、秩序相はそれぞれ、 次近接相互作用が斥力の場合、新たな秩序相が現れる。三角格子の場合には、この相は2x2構造をもっているが、従来の研究では、この相への転移は一次であると結論されていた。しかし、我々の方法を用いてかなり大きな系まで計算した結果、この転移は二次であり、しかも四状態Potts模型と同じユニバーサリティクラスに属することが明らかとなった。この結果は、この相の基底状態が四重縮退しているという事実と符合する。このクラスには、log型の補正項が存在することが知られており、そのため、かなり大きな系の計算が必要となる。また、 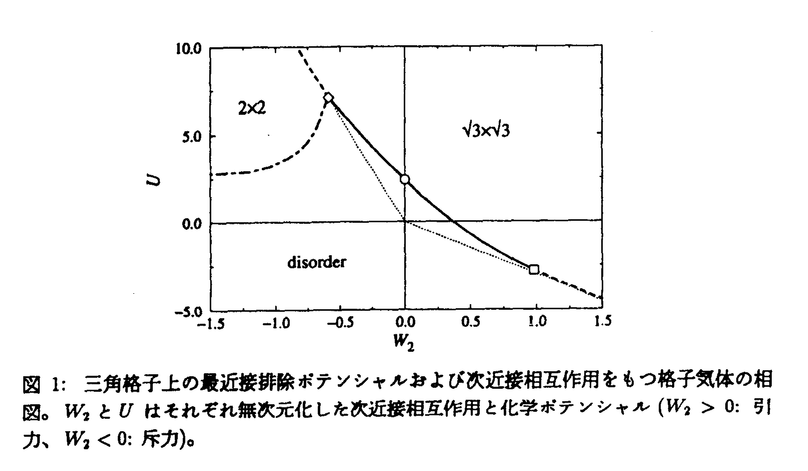 一方、正方格子の場合、2x1構造をもつ秩序相が現れる。この相は基底状態でO 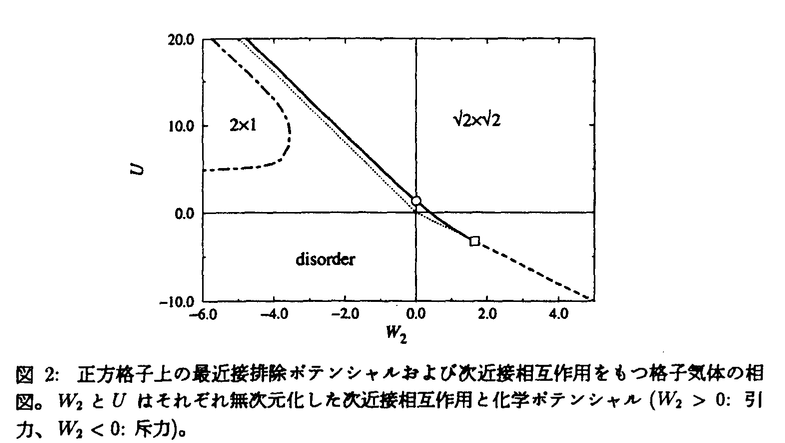 以上のように、従来よりも非常に大きな系を扱うことによって、さまざまな新しい結果が得られた。特に、純粋なハードコアポテンシャルのみの場合には、(2x1のような特殊な秩序相をもつ場合を除いて)基底状態の縮重度と転移のユニバーサリティクラスとの間には、Potts模型と同様の関係が成り立っていることが結論された。第三近接まで排除する模型では、基底状態の縮重度は5以上となり、したがって転移は一次となることが期待される。 第三章では、一次元のハードコアポテンシャルをもつ量子格子気体の基底状態相転移を議論する。この系のハミルトニアンは で定義される。ただし、Jk=∞(k=1,2,・・・,m-1)である。この系の秩序相はm重縮退しており、Potts模型との対応からはm 第四章では、連続空間上のハードコアポテンシャルのみをもつ粒子系の液相における状態方程式を二次元と三次元においてビリアル展開を用いて議論する。一般的に液相における状態方程式は、 の形の特異性を持っていると期待される。ビリアル展開についてパデ近似とコヒーレント異常法を用いた解析を行うことにより、特異点 一次元では、これら二つの密度は同じであり、我々の結果は、Tonksの厳密解と一致する。一方、二次元以上では、この 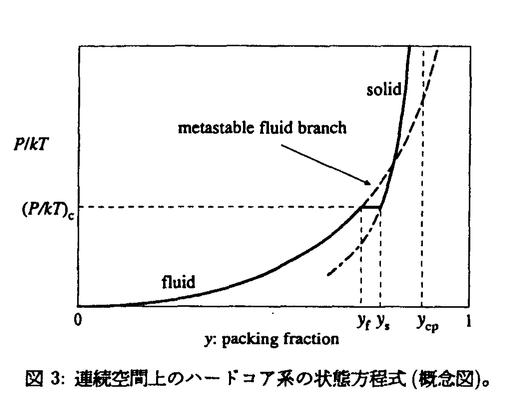 以上のように、本論文ではハードコア系の相転移について、いくつかの新しい結果が得られた。特に、二次元古典格子気体については、大規模な行列を取扱う方法を提案し、それを用いることによって、詳しい相図を得ることができた。最終の第五章では、それらの結果を簡潔にまとめる。 | |
| 審査要旨 | 本論文は5章からなる。第1章は一般的序論、第2章は2次元古典格子気体の相図、第3章は剛体ポテンシャルをもつ1次元量子格子気体の基底状態転移、第4章は連続空間上の剛体球系の状態方程式、第5章はまとめについて述べられている。 物質が示す3つの相(固相、液相、気相)の存在とそれらの間の相転移の解明は統計力学における最も基本的な問題の1つである。特に、固相と流体相(液相と固相の総称)の間の転移は常に1次転移であり、本質的に剛体球ポテンシャルで記述されると考えられている。実際、分子動力学法やモンテカルロ法によって、2、3次元の剛体球系における固相-流体相の1次転移の存在が確立されて既に30年以上になるが、その本質的な機構の物理的意味づけは明らかではない。本論文はこの状況に鑑み、離散空間上で定義された気体(格子気体)での斥カポテンシャルのもたらす効果と連続空間上での剛体球系の状態方程式の振舞いを研究した。 第2章では、2次元古典格子気体が転送行列法、現象論的繰り込み群、共形不変性などを用いて議論されている。模型には最近接排除ポテンシャルと次近接相互作用ポテンシャルが取り入れられている。そのために転送行列法では行列の次元が大幅に増大するため、数値計算においては系の大きさが制限されることになる。この困難さを克服するために、計算法の改良がなされた。すなわち、転送行列の要素のかなりの数が恒等的に零になるため、行列の次元を実質的に減らすことができて、こうして減らした行列の次元を再び少しだけ増やすことによって、次元の小さな疎行列に分解する方法である。この改良により、格子点の数NをN=35にまですることができた。この方法については付録に詳しく議論されている。上記の方法を用いて、最近接排除ポテンシャルおよび次近接相互作用をもつ2次元古典格子気体の相転移と臨界現象を調べ、詳しい相図を得た。特に、剛体ポテンシャルだけの場合には、基底状態の縮重度と転移のユニバーサリティクラスの間には、Potts模型と同様な関係が成り立っていることが指摘された。 第3章では、1次元剛体球系を記述する量子格子気体模型を用い、その基底状態と相転移を調べた。剛体球直径に相当する格子間隔数をm、格子点数をL、で表すと、固有値行列の対角化は、2 第4章では、連続空間上の剛体球系の流体相における状態方程式をビリアル展開から構成する試みが議論されている。既に知られているビリアル展開について、パデ近似とコヒーレント異常法を用いて状態方程式
の特異性を調べた。ここで、Pは圧力、kはボルツマン定数、Tは絶対温度、 以上のように、本論文は、固相液相の1次転移の機構解析を目指し、古典・量子格子気体の数値解析、剛体球系古典流体の状態方程式の提出、が行われている。特に、転送行列法における計算法の改良とそれに基づく相図の完成を評価する。固相液相転移自体は明確にとらえられたとは言えないが、統計力学におけるこの基本的な問題に対し、本論文は新しい知見を与えていると判定する。なお、本研究は鈴木増雄氏との共同研究であるが、論文提出者が主体となって計算解析を行ったもので、論文提出者の寄与が十分であると判断する。従って、審査員一同は、論文提出者に博士(理学)を授与できると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/53901 |
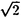 ×
×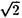 および
および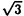 ×
×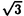 の構造をもち、その転移はIsing模型および三状態Potts模型と同じユニバーサリティクラスに属する。この系に次近接の引力を加えると、ある点(三重および四重臨界点)を境として転移が二次から一次へと変化する(図1,2)。
の構造をもち、その転移はIsing模型および三状態Potts模型と同じユニバーサリティクラスに属する。この系に次近接の引力を加えると、ある点(三重および四重臨界点)を境として転移が二次から一次へと変化する(図1,2)。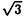 x
x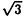 相と2x2相の共存線が存在し、その上では一次転移が起こることも示される。三本の相境界は八重臨界点で一点に交わる(図1)。
相と2x2相の共存線が存在し、その上では一次転移が起こることも示される。三本の相境界は八重臨界点で一点に交わる(図1)。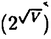 の縮重度をもつかなり特殊な状態である。転送行列を用いた従来の研究では、相境界上では臨界指数が連続的に変化するという非普遍的な振舞いが結論されていた。しかし、この秩序相のもつ対称性を考慮すると、この結果は、転送行列において誤った転送方向を選択したことによる「見かけの非普遍性」にすぎないことがわかる。「正しい」転送方向を用いた今回の計算によると、転移線に沿って臨界指数の変化しない、すなわち、普遍的な転移が結論される。また、三角格子上の場合とは対照的に、
の縮重度をもつかなり特殊な状態である。転送行列を用いた従来の研究では、相境界上では臨界指数が連続的に変化するという非普遍的な振舞いが結論されていた。しかし、この秩序相のもつ対称性を考慮すると、この結果は、転送行列において誤った転送方向を選択したことによる「見かけの非普遍性」にすぎないことがわかる。「正しい」転送方向を用いた今回の計算によると、転移線に沿って臨界指数の変化しない、すなわち、普遍的な転移が結論される。また、三角格子上の場合とは対照的に、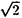 x
x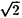 相と2x1相とは、有限温度で接することはなく、両者の間には常に無秩序相が存在することも明らかとなった(図2)。
相と2x1相とは、有限温度で接することはなく、両者の間には常に無秩序相が存在することも明らかとなった(図2)。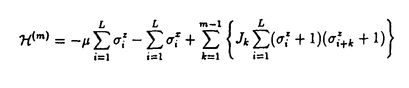
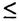 4では二次転移、m
4では二次転移、m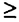 5では一次転移が期待される。一次元量子系の固有値行列は二次元の古典系の転送行列とは異なり、最初から疎な行列であるため、さらに容易に大きな系を扱うことができる。本論文では2
5では一次転移が期待される。一次元量子系の固有値行列は二次元の古典系の転送行列とは異なり、最初から疎な行列であるため、さらに容易に大きな系を扱うことができる。本論文では2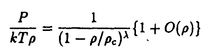
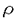 cは最密充填密度ではなく、充填率が1となる密度であることが示された。すたわち、液相において粒子は最密格子を形作った時の1粒子当たりの体積ではなく、粒子それ自身の体積によって有効的に排除されている。また、発散の指数
cは最密充填密度ではなく、充填率が1となる密度であることが示された。すたわち、液相において粒子は最密格子を形作った時の1粒子当たりの体積ではなく、粒子それ自身の体積によって有効的に排除されている。また、発散の指数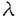 は系の次元と等しいことがわかる。
は系の次元と等しいことがわかる。