臨界現象においてはスケーリング則が一般に成り立つと考えられている。すなわち物理量の特異性が、発散の強さを表す臨界指数とスケーリング関数で表される。そして、この臨界指数とスケーリング関数は、系の基本的な対称性や次元だけで普遍的に決まると考えられている。

　本論文では、このスケーリング則を研究する対象として、任意のスピンSをもつ強磁性ハイゼンベルグ鎖を取り扱う。この系は磁性体のモデルとして頻繁に使われ、絶対温度T＝0で特異性をもつ。なお、系のハミルトニアンHを以下のように定義する。

　ここで、結合定数Jは正、そしてhは磁場を表わす。なお、境界条件として周期な場合と自由端の両方を考える。この系HのT＝0近傍で磁化mのスケーリング関数がSに寄らず同一の関数であるとの予想を立てた。実際に、線形帯磁率と非線形帯磁率のスケーリング関数を古典極限(S→∞)で求め、S＝1/2とS＝1の系の数値結果がそれに従うことを確認した。

　S＝1/2の熱力学的極限で、この系は、"熱力学的"ベーテ仮設をつかった数値計算が、行なわれていた。それによるとゼロ磁場の線形帯磁率₁の温度に関する特異性が₁〜1/T²(臨界指数＝2)、そして相関長の特異性が〜1/T(臨界指数＝1)と古典系と同じになることがわかっていた。

　われわれは、この古典系との類似性に着目し、さらに磁化の高次の磁場依存性を調べた。それには、"熱的"ベーテ仮設をつかった数値計算を使った。この方法は、先に行なわれていた"熱力学的"ベーテ仮設の方法より、より容易に自由エネルギーを計算できると期待されていた。これにより、ある温度Tと磁化mにおけるヘルムホルツの自由エネルギーgの値を得た。そしてこれがとm²で展開できると仮定し、その係数を最小二乗法により以下のように得ることができた。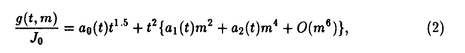

　ここで、J₀＝J/S²,t＝T/J₀.そして

　これより、ゼロ磁場の線形帯磁率₁を以下のように求めた。

　これは先の"熱力学的"ベーテ仮設による結果と一致した。さらに、ゼロ磁場の三次の非線形帯磁率₃の温度依存性も得られた。

　x≡Jh/T²を固定して、T→0の極限(スケーリング極限)では、xt^1/2,xt,x³t^1/2,x³t^1/2等の項を無視できる。Jh/T²の小さいところでの、磁化mのスケーリング極限の振る舞いは(6)と(7)より

　と書けることがわかった。一方、古典系でも₁と₃を解析計算し、Jh/T²の小さいところで磁化mのスケーリング極限の振る舞いを以下のごとく得た。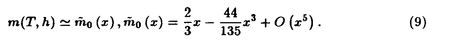

　ここで、(44/135)〜0.32なので、この古典系のスケーリング関数m₀は、S＝1/2の場合の(8)式と一致することが示せた。このように、熱力学的極限でS＝1/2,∞の系Hの磁化はあるスケーリング関数でかける。それらはスケーリング変数をxとして、このx³の項まで一致した。さらに、高次の項も一致するとして、S＝1/2,∞の系はxをスケーリング変数とする同一のスケーリング関数m₀で書けると予想した。なお、高次の項は、古典系より求められる。さらに他のスピンの場合もスケーリング関数がこのm₀になると予想とした。また、この(9)式はすべてのスピンで臨界指数＝＝2を意味する。

　次に、この予想を他のスピンで確認する。その際S＝1/2,∞以外で熱力学的極限の磁化を求めるのは困難である。故に有限サイズの系を考える必要が出てくる。われわれは、この系がT＝0で特異性を持つことからスケーリング関係式＝＝+1を任意のスピンで導いた。(この関係式はS＝1/2,∞では確認できる。)さらに先の予想からあらゆるスピンで＝1と期待できる。すると、系のサイズが相関長〜1/Tでスケールできると考えられる。これより長さに関するスケーリング変数としてy≡J/TLを導入する。そして、熱力学的極限のスケーリング関数(9)式を一般化して以下のようにかけると予想する。

　なお、熱力学的極限(T,hを固定して、L→∞)を取る操作はy→0とすることで実現できる。これより、以下の関係が導かれる。

　これよりm(x,y)がスピンによらず不変であれば、m₀(x)もスピンによらず不変となる。ここでは、スケールされた磁場xが有限な場合に磁化を調べるのは困難なので、熱力学的極限の時と同様にゼロ磁場の帯磁率を調べてみる。

　古典系で、ゼロ磁場(x＝0)の場合、周期及び自由端のいずれの境界条件でも分配関数、二点と四点相関関数、線形及び三次の帯磁率₁,₃を第二章で解析的に求めた。得られたこれらの物理量のスケーリング極限をとると、スケーリング変数yのみを含んだスケーリング関数でかけるを確認した。特に、₁,₃は(12)式を満たしている。これより、この₁と₃を古典系で解析的に求めた。

　ここで、前者は周期境界、後者は自由端である。

　は分配関数のスケーリング関数である。三次の帯磁率の周期境界のスケーリング関数はを使い次のように求められる。

　自由端の場合は次のようにスケーリング関数を古典系で解析的に得た。

　我々の予想にしたがえば、他のスピンでもこれら(14),(16),(17)式がスケーリング関数になる。

　次に、第三章では他のスピンとしてS＝1/2,1をとりあげ、第二章で得られたスケーリング関数(14),(16),(17)が満たされることを数値計算で示す。数値計算では、系のハミルトニアンHをハウスホルダー法で対角化して全エネルギー固有値を求める。これを使い相関関数を求め、それをすべてのサイトで和を取った。なお、系のサイズLはS＝1/2でL14,S＝1でL10である。図1で対角化より得られたS＝1/2の₁^periのデータをスケーリング極限への外挿を行なった。この際、S＝1/2の熱力学的極限の計算結果の解析(6)と(7)と同様にで展開できると仮定した。線形,三次の帯磁率を周期境界と自由端のあらゆる組み合わせに対してS＝1/2,1の系に同様の解析を行なう。そして、スケーリング極限に外挿し、スケーリング関数の値を得る。

図1:スケーリング関数に対する₁T²/Jの補正。S＝1/2周期境界の強磁性ハイゼンベルグ鎖。y＝J/(TL)＝0.5,1.0,1.5,2.0,2.5,3.0,5.0,L8.なお、補正はで展開できるとし、原点に近い方から三点を二次曲線で外挿した。

　こうやって得られたスケーリング極限における各スケーリング関数の値を図2,3,4,5にまとめた。

図表図2:周期境界条件の強磁性ハイゼンベルグ鎖の線形帯磁率のスケーリング関数₁^peri(y)。実線は古典系より解析的に得られた関数(14)。 / 図3:自由端の強磁性ハイゼンベルグ鎖の線形帯磁率のスクーリング関数₁^open(y)。実線は古典系より解析的に得られた関数(14)。 / 図4:周期境界の強磁性ハイゼンベルグ鎖の三次の非線形帯磁率のスケーリング関数₃^peri(y)。実線は古典系より解析的に得られた関数(16)。S＝1/2の熱力学的極限でのベーテ仮設による値₃^peri(y＝0)(x³の係数)(8)を示した。 / 図5:自由端の強磁性ハイゼンベルグ鎖の三次の非線形帯磁率のスケーリング関数₃^open(y)。実線は古典系より解析的に得られた関数(17)。

　第二章で任意のスピンでのスケーリング関数の解析的な形を求めるのに古典強磁性ハイゼンベルグ鎖を使った。第四章では、この周期境界の古典系を連続体に近似してスケーリング関数を得る。この際の計算は元の格子モデルより見通しがよくなる。さらに、この連続体モデルは有限範囲の長距離相互作用の場合にも応用できる可能性がある。古典強磁性ハイゼンベルグ鎖は、格子定数がゼロになる連続体極限では、次の"重力場"(x)中の球面上に束縛された一体の量子回転子モデルH_rotの温度yでの熱力学と解釈できる。

　このハミルトニアンH_rotはスケーリング変数x,yしか含まない。故に得られる物理量はスケーリング関数そのものと考えられる。実際にH_rotを使って、元の系Hの分配関数、相関関数、帯磁率を解析計算した。そしてこれらが、期待どおり格子モデルで得られた結果(14),(16)と同じになった。特に、格子模型の熱力学的極限y→0はH_rotの基底状態に相当する。この場合は、H_rotの行列要素が求まる。故に(9)式で与えられるm₀(x)が数値的にxの全てに対して求まる(図6参照)。この図にはS＝1/2のベーテ仮説からのデータも同時にプロットした。温度が下がるにつれ、m₀(x)に近づく様子が、定性的に確認できる。さらに、m₀(x)の漸近形が摂動論より左式のように求まる。このように、回転子モデルで強磁性ハイゼンベルグ鎖のスケーリング関数を求められることがわかった。故に、高次の相関長や帯磁率はこの方法を使い見通しよく求まると思われる。また、元のハミルトニアンHでスケーリング極限をとることは、連続体近似を取ることに相当することがわかった。

図6:連続体近似から得られたy＝0のスケーリング関数m₀とベーテ仮説に寄る計算結果。

　まとめると、本研究では任意のスピンの強磁性ハイゼンベルグ鎖がスピンによらない不変なスケーリング関数を持つことを予想した。S＝1/2,1,∞の系で解析的におよび数値的に厳密に物理量を計算し、それらがスケーリング極限で同じ値を取ることを示し、この予想を確認した。さらに、そのスケーリング関数が連続体近似の磁場中の量子回転子モデルより解析計算で求られることを示した。

　理学修士中村浩章提出の本論文は一次元強磁性ハイゼンベルグ模型の強磁性相転移のスケーリング関数を磁場中を含めて考察したもので、英文で5章から成る。

　一次元強磁性ハイゼンベルグ模型は絶対零度で強磁性相転移を起こし基底状態で強磁性秩序を示す。さらに温度をコントロールパラメタとして、有限温度で絶対零度に向かって帯磁率、強磁性相関距離などの物理量が臨界現象を示すことが知られている。一般には、転移点が絶対零度である連続相転移では、系の持つ量子性がこの臨界現象に影響を与えることが期待される。しかしこの相転移の場合には古典極限であるS＝∞の場合と、量子性の最も強いS＝1/2の場合とを比較すると、磁場ゼロの時に、知られている範囲で帯磁率や相関長の低温極限での低温展開の表式が臨界指数と係数を両方含めて一致することが知られていた。

　本論文提出者はまず磁化の磁場依存性のうち、磁場の3乗に比例する項から導かれる非線形帯磁率を計算した。S＝∞の場合は良く知られた手法を用い、またS＝1/2の場合は熱的ベーテ仮説に基づく連立方程式を数値的に解いて、両者の厳密解が3桁以下の数値誤差の範囲内で一致することを示した。この考察をもとに、本論文提出者は、低温極限では有限磁場での帯磁率、非線形帯磁率、さらには磁化がSの大きさ(量子性)に依らないのではないかという予想をもとに、いくつかの研究を行なった。

　まず磁場ゼロでの線形帯磁率についての研究について触れる。線形帯磁率が熱力学極限での表式だけでなく、有限サイズスケーリング関数も量子性に依らないのではないかという予想をたてて、S＝1/2の場合とS＝1の両方の場合について、コンピュータのメモリ制限の範囲内で有限クラスターのハミルトニアン行列の数値的な対角化を行ない、S＝∞の場合と比較した。この際、低温極限に限定した議論を行なうために、磁場に関わるスケーリング変数Jh/T²(ただしJは交換相互作用の大きさ、hは磁場、Tは温度)を一定に保って、温度補正が温度の1/2乗で展開できるという仮定のもとに、温度ゼロの極限(スケーリング極限)をとり、この極限での比較をおこなった。結果をまとめると、有限サイズ補正のスケーリング変数J/TL(ただしLは系の長さ)が十分小さい、すなわち熱力学極限の近くに関しては数値対角化が行なえないために明らかでないという限界があるものの(ただしS＝1/2の場合にJ/TL＝0の極限はベーテ仮説に基づく結果がありS＝1/2の場合とS＝∞の場合が一致することは知られている)、概ね有限サイズスケーリング関数の関数形がS＝1/2、S＝1、S＝∞のすべての場合によく一致するという結果を得た。これは量子性の違う3通りの場合に、ここで議論した有限サイズスケーリング関数が量子性に依存しないことを示唆する結果となっている。

　次に磁場ゼロでの非線形帯磁率についての研究について触れる。この場合も線形帯磁率の場合と同じ手法によって、有限サイズスケーリング関数のサイズ依存性を議論した。この場合は数値対角化で取り扱った系のサイズの限界に起因して、スケーリング極限をうまくとれる範囲が限定されたため、有限サイズスケーリング変数のかなり大きな範囲に限定されるものの、調べた範囲内では、やはり有限サイズスケーリング関数の関数形がS＝1/2、S＝1、S＝∞のすべての場合によく一致するという結果を得た。

　また本論文提出者は、古典極限でのハイゼンベルグ模型の絶対零度近傍の性質を議論するときに、相関長が長いため、離散的な格子の効果を無視した連続極限をとって良いという妥当な仮定をおき、この連続極限で古典ハイゼンベルグ模型が、重力場中の球面上に束縛された一体の量子回転子模型に等価であることを用いて、磁化曲線をこの極限で厳密に求めた。一方S＝1/2でベーテ仮説に基づく厳密な磁化曲線を有限温度で求め、低温になるほど、量子回転子模型で得られた数値的な結果に近づくように見えるという結果を得た。しかしS＝1/2の場合に十分に低い温度での結果を得ていないため、この一致は十分に説得力のあるものとはなっていない。

　以上述べてきたように、この論文では、低温極限で、有限磁場での帯磁率、非線形帯磁率、さらには磁化が、Sの大きさ(量子性)に依らず、スケーリング関数の関数形まで含めて、古典極限でのふるまいによって、普遍的に記述されるのではないかという興味ある予想をもとに、いくつかの研究を行なったものである。今まで詳しく述べたことからわかるように、この論文だけからこの予想が検証されたわけではない。特に非線形帯磁率に関する有限サイズスケーリング関数の普遍性や磁化曲線の絶対零度での量子効果の検討、普遍性のより一般的な導出など今後の課題は多い。一方、低温での磁場ゼロでの線形帯磁率について、有限サイズスケーリング関数の関数形がS＝1/2、S＝1、S＝∞のすべての場合に数値的な範囲内でよく一致するという結果や、量子回転子模型を用いてこの予想が正しいとしたときの普遍的な磁化曲線を簡単かつ厳密に求める手法と結果を提示した点などに、この予想の検証をめざした一定の成果が認められる。

　以上の問題点や一定の成果について種々議論した結果、合議の上、本論文審査委員会によって、本研究は博士(理学)の学位論文として合格として判定された。

　なお本研究は、指導教官高橋実教授、羽田野直道博士、S.Sachdev教授との共同研究の部分があるが、主要部分について論文提出者が主たる寄与をなしたものであることが認められた。