数値流体力学に限らず、計算科学諸分野において計算機能力向上が叫ばれている。こうした中で今後計算機の主流となるのは超並列計算機であると考えられている。プロセッサ数は増加の一途をたどり、近い将来数十万〜数百万プロセッサをもった超並列計算機が現れるといわれている。 一般に並列計算においてプロセッサ数が増加して粒度が低下すると、解の収束性、並列化効率ともに悪化してしまう。多重格子法(multigrid method)を導入してさらなる高速化を図ることにより、こうした問題点を乗り越えようとする試みが多くの研究者によってなされ、一定の成功を収めている。しかし、さらに粒度が低下した場合、多重格子法の並列化効率は通常の解法よりも激しく下落してしまうことが指摘されている。したがって、超並列コンピュータの性能を十分に引き出す決定的な数値計算手法は確立されていないのが現状である。 そこで本研究では、非圧縮性流れを超並列計算機上で数値解析するのに適した計算手法を提案することを目的とした。まず最初に、筆者は超並列計算コードに要求される要件として、以下の4項目を整理した。 1.高い並列性をもつこと 2.収束性が良いこと 3.プロセッサ通信が少ないこと 4.簡便なアルゴリズムであること 上に挙げた4項目を考慮して、数値計算手法として次の手法を選択した。 1.並列化手法:領域分割法(domain decomposition method) 2.流れ計算手法:連立解法(coupled method) 3.加速手法:外挿法(extrapolation method) 連立解法は、運動方程式と連続の式を直接連立させて解く手法であり、従来よく用いられてきたMAC系解法やSIMPLE系解法などに比べると簡便性において優れた手法である。また、領域分割法と組み合わせると並列性が高い。一方、外挿法は、解のたどった履歴から収束値を予測する加速手法である。これは、プロセッサ通信をほどんど必要とせず、ソルバーとまったく独立な数値的操作であるために粒度が小さくなっても加速率がほとんど低下しない。したがって、超並列計算に適した加速手法と考えられる。 外挿法は、線形代数方程式を繰り返し法により解く場合、k回目の繰り返し操作の結果得られる途中解xkが、系の固有値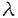 iと固有ベクトル iと固有ベクトル iにより以下のように展開されるという事実に基づいている。 iにより以下のように展開されるという事実に基づいている。  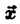 は収束解、aiは初期値により決まるスカラー係数、Nは系の自由度である。式(1)の右辺第2項は、誤差に相当する。外挿法はこれらの誤差のうち収束の遅いもの、すなわち絶対値が1に近い固有値に相当する成分のみが支配的であると仮定して、解の履歴の変化の様子より収束値xを予測する手法である。既存の外挿法には様々な種類があり、本研究で取り上げたものはROLE(Ratio Operated Local Extrapolation)、MPE(Minimal Polynomial Extrapolation)、ROGE(Ration Operated Grain Extrapolation)と呼ばれるものである。ROLEは一つの格子点における履歴のみを参照するもの、ROGEは領域分割された小領域内に属する格子点の履歴のみを参照して各プロセッサ毎に独立に外挿を行うもの、MPEは全格子点の履歴を参照するものである。 は収束解、aiは初期値により決まるスカラー係数、Nは系の自由度である。式(1)の右辺第2項は、誤差に相当する。外挿法はこれらの誤差のうち収束の遅いもの、すなわち絶対値が1に近い固有値に相当する成分のみが支配的であると仮定して、解の履歴の変化の様子より収束値xを予測する手法である。既存の外挿法には様々な種類があり、本研究で取り上げたものはROLE(Ratio Operated Local Extrapolation)、MPE(Minimal Polynomial Extrapolation)、ROGE(Ration Operated Grain Extrapolation)と呼ばれるものである。ROLEは一つの格子点における履歴のみを参照するもの、ROGEは領域分割された小領域内に属する格子点の履歴のみを参照して各プロセッサ毎に独立に外挿を行うもの、MPEは全格子点の履歴を参照するものである。 上で述べたように、外挿法は比較的収束の早い中・短波長の波は支配的でないとして無視し、長波長誤差のみを考慮する。ところが、実際には中・短波長の波が完全に減衰していることはほとんど有り得ないので、この仮定が外挿による加速効果を損なう一因となっている。したがって、長波長を中・短波長から分離して、外挿の効果は大きくなるはずである。そこで本研究では既存の外挿法をベースにして新たな外挿法LWE(Long Wave Extrapolation)を開発した。すなわち、  のような正弦波を考え、比較的波数の少ない数十程度の波を抽出して短波長の波と分離した形で外挿を行うのがLWEである。 外挿法の性質を確かめるために、256×256の格子でポアソン方程式をRed-Black SOR法で解く並列計算コードに外挿法ROLEとLWEを導入した。その結果、256プロセッサを使った場合、ROLEによる加速率が約2.0倍、LWEによる加速率が約3.3倍であった。プロセッサ数が512に増加した場合でもROLEの加速率は約2.4倍、LWEの加速率は約3.0倍であり、両者の加速率はあまり変化しない。多重格子法を用いると、この計算よりも大きな粒度である場合でも著しく効率が低下して、加速率が1.3倍程度になってしまうという研究例もあり、外挿法が粒度の小さい超並列計算に適していることを示している結果といえる。 以上において述べてきた外挿法は、元来線形方程式向けに開発された加速手法である。したがって、ナビエ・ストークス方程式のように、非線形項を含む方程式の数値解法にそのまま適用することはできない。そこで、本研究では不動点近傍における非線形写像の挙動を詳しく調べ、固有値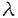 iに対応する固有ベクトル成分は、以下の式の形で表現できることを見出した。 iに対応する固有ベクトル成分は、以下の式の形で表現できることを見出した。  式(3)の第2項目は、固有値の二次形式であり、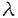 i i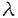 jは実質的に固有値として振舞う。系全体としては、実質的な固有値の個数がN(N+1)/2だけ増えたことと等価である。したがって、非線形方程式であっても、外挿法を適用することは可能である。しかし、非線形性により系の実質的自由度が増えているので、 jは実質的に固有値として振舞う。系全体としては、実質的な固有値の個数がN(N+1)/2だけ増えたことと等価である。したがって、非線形方程式であっても、外挿法を適用することは可能である。しかし、非線形性により系の実質的自由度が増えているので、 ・考慮する固有値の個数を線形方程式の場合より多くする。 ・解を保存するステップ数を大きくして、大きな固有値成分を抽出しやすくする という2点に留意しなければならない。 以上のような議論を踏まえて、連立解法による非圧縮性Navier-Stokes方程式の超並列計算に外挿法を導入するコードを開発し、その超並列計算への適合性を検討した。使用した超並列計算機は富士通のAP1000であり、プロセッサ数は256および512である。計算対象とするのは、正方形キャビティ内流れ(Re=100とRe=1000)と片側急拡大流れで、格子点数はキャビティ流れが256×256、急拡大流れが256×128である。なお、外挿法を十万自由度にも及ぶ非線形問題に適用し、さらにそれを超並列計算に適用した研究は、本研究が初めてである。本研究での計算結果から得られた結論は以下のようになる。 ・レイノルズ数が大きい場合、考慮しなければならない固有値の個数が増加するが、際限なくpの値を大きくするわけにはいかない。そこで、pの値が小さくても加速効果が大きくなるように外挿法を改良していくことが必要である。 ・繰り返し数の減少率では、LWEが概ね優れていた。これは、長波長成分を抽出することの効果が現れたものと考えられる。しかし、その優位性は他の外挿法に比べて取り立てて大きいわけではない。抽出する長波長成分をどのような形にするかについて今後の検討が必要である。 ・キャビティ流れ(Re=1000)では約1.6〜1.7倍、キャビティ流れ(Re=100)では約1.9〜2倍、急拡大流れでは約2〜2.1倍という正味の加速率を得ることができた。計算打ち切り残差を小さな値に設定することによりさらなる加速効果を期待できる。 ・多重格子法は、極細粒度になると通信負荷が卓越するため効率が著しく低下するのに対し、外挿法は安定した加速性能を保つ。したがって、超並列計算における加速手法として外挿法は有望である。 ・高い並列性をもつ連立解法に外挿法を導入する手法は、まだ実用の域には達していないものの、超並列計算における非圧縮性流れ計算コードの進むべき一つの方向性を強く示唆している。 |