| 内容要旨 | | 等スペクトル力学系(Isospectral flow)とは,正方行列の集合上をその固有値を保ちながら時間発展する力学系であり,Lax形式  で表される.Lax形式の力学系自体は古くから研究されてきたが,1991年のBrockettによる2重Lax形式の力学系  の発見以来,完全可積分系(ソリトン系)との関連,固有値計算アルゴリズムへの応用の観点から,研究が再燃してきた. さらにその後,本来確率分布のなす空間の自然な幾何学的構造として研究されてきた情報幾何学と,完全可積分系の間に,なんらかの本質的な関連があることを示唆するいくつかの例が発見された.これらの例がLax形式の力学系で表されることから,Lax形式の力学系を軸としてこれら2つの分野を関連づける研究が試みられてきた. 本論文は,これらのLax形式の力学系の研究に対して,いくつかの視点からの一般化を行ない,すでに発見されている散発的な例を統一的な立場から理解することを試みるものである. まず,一般のポテンシャル関数の勾配系として表される複素行列の空間上の等スペクトル力学系の一般式を求めると,  となる.この一般式から,これまでに発見されていた等スペクトル力学系の例であるBrockettの方程式,行列版のToda方程式,Nakamuraの方程式が導かれる.これより,これらの例がともに2重括弧形式で表されることが単なる偶然ではないことが明らかになる.さらに,得られた一般式から非対称行列の固有値問題のための新しい力学系の例を構成することができる. また,上の一般式を求めるのに用いた計量とは異なる計量に関する等スペクトルな勾配系の式を求めると,これは多重括弧形式で表される.その一つの例であるBrockettの2重括弧形式の力学系の多重化 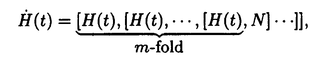 は,多重度mが偶数であるときBrockettの2重括弧形式の力学系と同じ不動点に収束し,多重度mが奇数であるときは漸近安定な不動点を持たない. 階数1の行列からなる随伴軌道に対して,各行列の対角成分を 1, 1, 2,・・・ 2,・・・ nとし,ポテンシャル関数 nとし,ポテンシャル関数  で定義される双対幾何構造を導入すると,この随伴軌道上のBrockettの力学系はこの双対幾何構造に関する双対座標系で線形化される.MoserがToda方程式の分析のために導入した力学系は,階数1の随伴軌道上のBrockettの力学系のひとつの例であり,したがってこれも同様にルジャンドル変換で線形化される. フルランクの行列からなる随伴軌道上に適切な双対幾何構造を導入し,その双対座標系で等スペクトル力学系を線形化すること,及び,その双対幾何構造を用いて完全可積分系に対し新たな幾何学的視点を導入することが今後の課題である. |
| 審査要旨 | | 本論文は「A Mathematical Study on Eigenvalue-Preserving Matrix Dynamical Systems(固有値を保存する行列力学系の数理工学的研究)」と題し,5つの章からなる. 等スペクトル力学系(Isospectral flow)とは,正方行列の集合上をその固有値を保ちながら時間発展する力学系であり,Lax形式で表される.Lax形式の力学系自体は古くから研究されてきたが,1991年のBrockettによる2重Lax形式の力学系の発見以来,完全可積分系(ソリトン系)との関連,固有値計算アルゴリズムへの応用の観点から,研究が再燃してきた. さらにその後,本来確率分布のなす空間の自然な幾何学的構造として研究されてきた情報幾何学と,完全可積分系の間に,なんらかの本質的な関連があることを示唆するいくつかの例が発見された.これらの例がLax形式の力学系で表されることから,Lax形式の力学系を軸としてこれら2つの分野を関連づける研究が試みられてきた. 本論文は,これらのLax形式の力学系の研究に対して,いくつかの視点からの一般化を行ない,すでに発見されている散発的な例を統一的な立場から理解することを試みたものである.すなわち,第2章では勾配系として表されるLax形式の力学系を一般的に考察し,第3章では2重Lax形式の多重Lax形式への一般化を行ない,第4章では行列の空間に対して新しい双対幾何構造を導入しLax形式の力学系と情報幾何学の関連を一般的に理解することを試みている. 以下に各章の概要をまとめる. 第1章「Introduction」では,等スペクトル力学系,Lax形式の力学系の基本的な性質,及びそれらの数理工学の諸問題との関連について概観し,最後に本論文の構成について述べている. 第2章「Isospectral Flows of Double Bracket Forms」では,一般のポテンシャル関数の勾配系として表される等スペクトル力学系の一般式を導き,これが一般的に2重括弧形式で表されることを示している.また,これまで散発的に発見されてきた等スペクトル力学系の例がこの一般式から統一的な視点で導かれることを示し,さらに得られた一般式から非対称行列の固有値問題のための新しい力学系の例を構成している. 第3章「Isospectral Flows of Multiple Bracket Forms」では,第2章とは異なった計量に関する等スペクトル勾配系が多重括弧形式で表されることを示し,その一つの例としてBrockettの2重括弧形式の力学系の多重化の性質について詳しく論じている. 第4章「Isospectral Flows and Dualistic Geometry」では,双対幾何学の基本的な事項,及び双対幾何学と等スペクトル力学系に関するこれまでの研究を概観した後,階数1の随伴軌道上のBrockett’s flowが,情報幾何学における多項分布の空間のルジャンドル変換によって線形化されることを示している.またMoserがToda方程式の分析のために導入した力学系が階数1の随伴軌道上のBrockett’s flowであること,したがってこれも同様にルジャンドル変換で線形化されることを示している. 第5章「Conclusion」では,本論文で得られた新しい知見のまとめと,今後の研究の方向づけとしてLax形式の力学系を軸とする情報幾何学とソリトン理論の関連づけに関する展望が述べられている. これを要するに,本論文は現在発展しつつあるLax形式の力学系の理論に対し,いくつかの統一的な視点を与えたもので,数理工学,情報工学に貢献する所が大きい.よって本論文は博士(工学)の学位論文として合格と認める. |