論文の表題は毛細管曲面の曲率発展方程式の内点における微分の爆発についてである。本論文において提出者は、下記の準線形発展方程式を研究した。 ただし、Duはu の微分、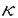 は正の定数、BRはn次元ユークリッド空間Rnの半径Rの円盤、u0はBR上の関数で原点に関して対称であるとする。 は正の定数、BRはn次元ユークリッド空間Rnの半径Rの円盤、u0はBR上の関数で原点に関して対称であるとする。 最近、非線形発展方程式における解の微分の爆発の研究が大きな発展を遂げてきてきている。上記の方程式の定常解が水滴の表面を表していることに気を付ければ、初期関数u0によって微分の爆発が起こる場合と起こらない場合とがあることが推察される。u0に比べてRが十分大きければ上記方程式は有限時間内に定常解になることが証明されて物理的に観察されることに一致する。一方で提出論文ではある意味で逆の場合には必ず微分の爆発が起こることを証明した。 結果を述べるためにまず下記の如く関数のあるクラスを定義する: 定義「原点の回りでの急減少関数」 区間I=[-R,R]上の非負なC1の関数u0(r)で、原点対称なものを考える。この様なu0(r)が、原点の回りで急減少であるとは、正定数の組(a,m,M,N)が存在して、次の(i)から(iv)を満たすときをいう。 ただし、、またt1は、mとMにより定まる正定数である。 提出者は、BR上のtと共に自己同形に変化するトーラスを比較関数として採用することにより、まず次の定理を証明する事が出来た。この定理は、解の最大存在時間が急減少な初期関数により制御されることを示すものである。 定理1 (1.1)-(1.3)を仮定し、更に初期関数u0は回転対称で、[-R,R]上の関数と見たときに、上述の急減少関数の定義を満たすとする。このとき、解の最大存在時間T0は、 を満たす。ただし、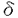 とLは、上で定義したものとする。 とLは、上で定義したものとする。 また次の定理は、実際に内点で解の微分が爆発することを証明したものである。この際、補題として、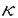 に条件をつけることなく|u(r,t)|を評価した。 に条件をつけることなく|u(r,t)|を評価した。 定理2 定理1と同じ仮定をおく。更に、m>4/Rを仮定する。このとき、ある初期関数u0が存在して、 が、解の最大存在時間T0について成立する。 上記の方程式が初期関数によって実際に爆発が起こることを巧みにしめしており比較関数の発見に独創的なアイデアがある。 以上によって、論文提出者 浅井 景粋は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |