| 内容要旨 | | Gを半単純Lie群,H1,H2をGの閉部分群とする.(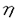 , ,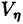 ),( ),(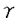 , ,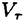 )をそれぞれH1,H2の有限次元既約表現としたとき, )をそれぞれH1,H2の有限次元既約表現としたとき, 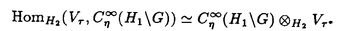 の元をtype-(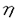 , ,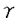 )の球函数と呼ぶ.ここで )の球函数と呼ぶ.ここで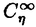 (H1\G)は (H1\G)は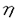 に付随したH1\G上の等質ベクトル束のsmooth sectionの空間で, に付随したH1\G上の等質ベクトル束のsmooth sectionの空間で,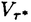 は は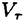 の反傾表現. の反傾表現. 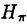 をGのadmissible表現とし, をGのadmissible表現とし,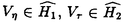 を を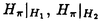 の既約成分とする.この時, の既約成分とする.この時, 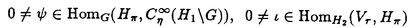 とおくと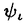 = =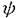 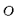 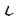 はtype-( はtype-(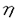 , ,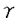 )のnon-trivialな球函数となり,特に )のnon-trivialな球函数となり,特に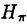 に付随した球函数と呼ばれる. に付随した球函数と呼ばれる. この球函数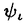 は以下のように記述される. は以下のように記述される. 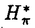 を を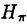 の反傾表現とする.またH1-mapi1,H2-mapj2を の反傾表現とする.またH1-mapi1,H2-mapj2を 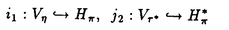 なるものとする. 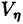 の基底を の基底を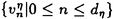 , ,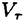 の基底を の基底を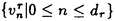 とし,その双対基底をそれぞれ とし,その双対基底をそれぞれ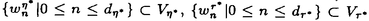 とする.この時, とする.この時,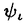 は は 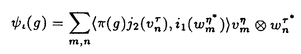 と書ける.特に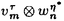 の係数 の係数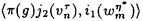 をmatrix coefficientと呼ぶ. をmatrix coefficientと呼ぶ. 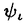 をtype-( をtype-(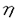 , ,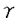 )の球函数とすると,g∈G,h1∈H1,h2∈H2に対して )の球函数とすると,g∈G,h1∈H1,h2∈H2に対して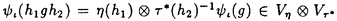 が定義より成り立つから, が定義より成り立つから,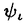 はH1\G/H2上への制限で決定される. はH1\G/H2上への制限で決定される. 本論文はG=Sp(2,R),H1=H2=K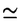 U(2)をGの極大コンパクト部分群とし, U(2)をGの極大コンパクト部分群とし,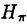 が主系列表現 が主系列表現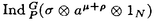 と一般主系列表現 と一般主系列表現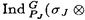 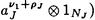 の2つの場合に,その球函数が満たす微分方程式系を具体的に書き表し,その級数展開と積分表示を得ることを目的とした,ここでP=MANはGの極小放物型部分群,PJ=MJAJNJはJacobi型の極大放物型部分群であり, の2つの場合に,その球函数が満たす微分方程式系を具体的に書き表し,その級数展開と積分表示を得ることを目的とした,ここでP=MANはGの極小放物型部分群,PJ=MJAJNJはJacobi型の極大放物型部分群であり,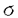 ∈ ∈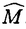 , ,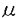 + +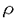 ∈Lie(A) ∈Lie(A)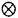 RC, RC,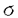 JはMJの離散系列表現, JはMJの離散系列表現,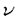 J+ J+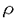 J∈Lie(AJ) J∈Lie(AJ)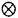 RCである.また, RCである.また,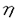 , ,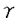 としては としては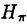 に含まれるK-typeの中で次元が最小となるものを選ぶ.すると に含まれるK-typeの中で次元が最小となるものを選ぶ.すると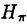 のparameter次第でd:=dim のparameter次第でd:=dim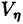 =dim =dim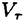 =1または2となる. =1または2となる. 球函数はK\G/K⊂R2上で決定されるので,得られる微分方程式系は2変数の偏微分方程式系になる.d=2では球函数はvector値なので行列型の偏微分方程式系が得られる.微分方程式系は2式からなり,それらはCasimir operatorとShift operatorから得られる.Shift operatorとは,球函数のK-typeをshiftする作用素で,Schmid operatorと呼ばれるK-covariantな作用素を用いて定義される.Casimir operatorもShift operatorもd=1の時はU(g)の元,d=2の時はU(g)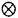 End(C2)の元である.ここで,U(g)はg=Lie(G)のenveloping algebraとする. End(C2)の元である.ここで,U(g)はg=Lie(G)のenveloping algebraとする. KoornwinderやHeckman-Opdamの理論ではRiemann対称空間上のCasimir作用素において,各root 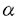 のmultiplicity のmultiplicity 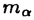 ∈Zを複素parameter ∈Zを複素parameter 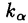 に拡張したものを考えている.彼らが導入したShift operatorはこの に拡張したものを考えている.彼らが導入したShift operatorはこの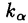 をshiftするoperatorで,我々が定義したものとは意味付けが異なっているが,彼らのBC型Shift operatorは本論文でのd=1の時のShift operatorと一致する.本論文での意味付けによるShift operatorの名称は宮崎-織田による. をshiftするoperatorで,我々が定義したものとは意味付けが異なっているが,彼らのBC型Shift operatorは本論文でのd=1の時のShift operatorと一致する.本論文での意味付けによるShift operatorの名称は宮崎-織田による. 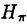 が主系列表現でd=1の場合,2階と4階の偏微分方程式が得られる.d=2の場合は2×2行列型の2階の偏微分方程式が2つ得られる. が主系列表現でd=1の場合,2階と4階の偏微分方程式が得られる.d=2の場合は2×2行列型の2階の偏微分方程式が2つ得られる. また,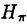 が一般主系列表現の場合の微分方程式系はd=2の場合でも球函数の成分,即ちmatrix coefficientを分離できて,scalar値の微分方程式が得られる.そして,dが1,2どちらの場合も適当な函数で共役を取ると次の形の微分方程式系になる. が一般主系列表現の場合の微分方程式系はd=2の場合でも球函数の成分,即ちmatrix coefficientを分離できて,scalar値の微分方程式が得られる.そして,dが1,2どちらの場合も適当な函数で共役を取ると次の形の微分方程式系になる. 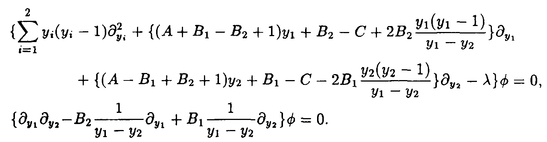 ここに現れるParameterA,B1,B2,C,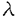 は は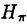 のparameterに依存する定数である. のparameterに依存する定数である. この偏微分方程式系の原点の近傍で正則な解の級数表示と積分表示は以下で与えられることが示せる. 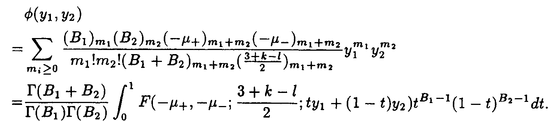 ここで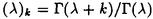 と定め, と定め,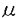 ±, ±,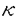 ,lは ,lは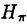 と と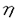 , ,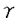 のparameterから決まる定数で,FはGaussの超幾何函数.この超幾何級数は のparameterから決まる定数で,FはGaussの超幾何函数.この超幾何級数は 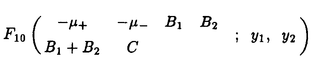 と書かれ,Appellの超幾何函数F1の一般化になっている. さらに,得られた微分方程式系がなす左idealは適当な変数変換と共役をとることによりAppellの超幾何函数F2が満たす微分方程式系の左idealに一致することが示せる.これによりF10の接続公式 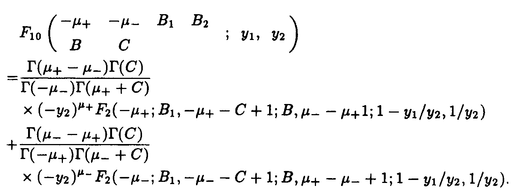 を導いた.ここでB=B1+B2とし,F2はAppellの超幾何函数で,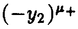 と と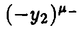 は|arg(-y2)|< は|arg(-y2)|<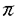 で定義する. で定義する. F10がAppellの超幾何函数F1の一般化になっていることから,系としてAppellの超幾何関数F1とF2の接続公式を得ることができる.それはKummerによるGaussの超幾何函数の接続公式の2変数への拡張である. |
| 審査要旨 | | 実半単純Lie群、あるいは、リーマン対称空間に対して定義される帯球関数は、Harish-ChandraおよびHelgasonにより一般論が確立された。帯球関数は、それの動径成分への制限で決まるが、それはLegendre関数などを拡張した多変数の超幾何関数となり、表現論的手法により、微分方程式による特徴づけや、関数の積分表示などが一般的に得られている。 一方、帯球関数は超幾何関数としてのパラメータが離散的であり、それを連続に拡張する試みが関口次郎、Heckman-Opdamによってなされ、数理物理における完全積分可能量子系や量子群と関連した球関数の理論と結び付いて、近年急速に理論が発展し、多くの研究が行われている。 帯球関数は、半単純リー群Gの既約表現で、その極大コンパクト部分群Kにより固定されるベクトルを持つものに対し定まり、K-不変ベクトルに対応する表現の行列要素と見なすことができる。一般のKの表現に対する行列要素は球関数と呼ばれるが、帯球関数と比べて、微分方程式がベクトル値になるなどの理由で今まで研究が十分に進んでいなかった。帯球関数に関連した上記のような最近の豊富な理論的発展を考えたとき、一般の球関数の場合に対応することがどうなっているか、具体的解明が課題となっていた。 論文提出者飯田正敏は、G=Sp(2,R)のある主系列表現の場合に球関数を研究した。提出論文において、具体的に動径成分の満たす微分方程式を決定し、原点における巾級数展開を求め、関数の積分表示を与えた。また、古典的な2変数の超幾何関数であるAppellのF1やF2との関係を明らかにした。 Lie群G=Sp(2,R)の極小放物型部分群をP、Jacobi放物型部分群をPJとする。Pの一次元表現から誘導したGの表現、すなわち最連続主系列表現をH0、またPJの相対離散系列表現から誘導した主系列表現をH1とする。提出論文では、この表現H0とH1に関し、Gの極大コンパクト群K=U(2)の表現として最も次元の小さいベクトルに対応する行列要素を考察した。 満たすべき微分方程式の具体形を求めることが、最初の課題である。まずGのCasimir作用素から2階の微分方程式が得られる。球関数の動径成分は2変数の関数なので、それを特徴づけるには別の独立した微分方程式が必要である。これは、誘導表現に現れるK-typeを調べ、K-typeをshiftするSchmid作用素を用いることにより具体的に構成されている。この手法は、帯球関数の場合にHeckman-Opdamが定義したshift operatorに対応するものであり、山下、宮崎-織田などによる研究でも使われていた。 主系列表現のパラメータに応じて、K-typeの最小次元dは1と2の場合に分かれる。H0の場合は、d=1の場合は2階と4階の、d=2の場合は2つの2階の2×2行列型の微分方程式が得られ、H1の場合は、どちらの場合も適当な変換により、2つの2階の方程式が得られる。これらは複雑な計算を遂行して初めて求められるが、論文提出者の得た方程式は極めて具体的に表示されており、特にH1の場合は2階のスカラー値の微分作用素で表せるので興味深い。 後者については、微分方程式の具体系を用いて、原点で正則な解の原点での巾級数展開が求められ、さらに一次式の巾積による2重積分表示が得られている。この超幾何級数がAppellのF1の一般化になっていること、および、求めた微分方程式がAppellのF2に変形できることから、応用としてF1とF2の間の接続公式を証明している。 論文提出者が扱った球関数は、Heckman-Opdamが扱った一般超幾何関数に収まらない例を与えている。帯球関数以外の球関数においても、具体的に超幾何関数としての研究が可能なことを示した初めての本質的例と言えるであろう。今後、一般論を作っていく上での良い指針になると推測される。 よって本論文提出者飯田正敏は、博士(数理科学)の学位をうけるにふさわしい十分な資格があると認める。 |