学位論文要旨
| No | 112107 | |
| 著者(漢字) | 藤岡,敦 | |
| 著者(英字) | Fujioka,Atsushi | |
| 著者(カナ) | フジオカ,アツシ | |
| 標題(和) | H曲面へのループ群の作用 | |
| 標題(洋) | Actions of loop groups on H-Surfaces | |
| 報告番号 | 112107 | |
| 報告番号 | 甲12107 | |
| 学位授与日 | 1996.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第42号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | 近年、リーマン面からリー群、あるいは、対称空間への調和写像の埋論は、大きな発展をとげている。例えば、調和写像の空間へのループ群の作用の発見は重要な役割を果たし、Bergvelt-Guest、Burstall-Pedit、Guest-大仁田、Uhlenbeck等の仕事が挙げられる。特に、Burstall-Peditの結果の特別な場合として、単連結リーマン面から三次元標準球面S3への調和写像の空間に、四次特殊直交群SO(4)のあるループ群が作用することが分かる。 Mを単連結リーマン面、 で定める。 が定義される。ここで、*はMのホッジスター作用素である。また、nfはframing Fのとり方に依らない。 p0∈Mを固定し、o={Kc}とおく。H,c∈Rに対し、 と定める。HH,cの元をH曲面と呼ぶことにする。CH,cはMから MからS3への調和写像は、H=0、c=1に対する 定理1.t∈Rに対し、 とおく。H,H’,c,c’∈Rに対し、sign(H2+c)=sign(H’2+c’)ならば、全単射 従って、上で定められるべきループ群の作用に関して、 本論文では、これらの予想が正しいことを示した。即ち、次の定理を得た。 定埋2.H,H’,c,c’∈Rがsign(H2+c)=sign(H’2+c’)を満たすとする。このとき、次の(i)-(iv)を満たすようなHH,cに作用する群 (i) (ii)リー群としての同型 (iii)定埋1の (iv) | |
| 審査要旨 | 論文の表題は、H曲面へのループ群の作用である。近年、リーマン面からり一群、あるいは、対称空間への調和写像の理論は、大きな発展をとげている。 Mを単連結リーマン面、
で定める。
が定義される。ここで、*はMのホッジスター作用素である。また、nfはframing Fのとり方に依らない。 p0∈Mを固定し、o={Kc}とおく。H,c∈Rに対し、
と定める。HH,cの元をH曲面と呼ぶことにする。CH,cはMからH3(c)への平均曲率一定Hのbranched conformal immersion全体の空間である。 MからS3への調和写像は、H=0、c=1に対する 一方、提出者の以前の論文で次の定理が示された。 定理1.t∈Rに対し、
とおく。H,H’,c,c’∈Rに対し、sign(H2+c)=sign(H’2+c’)ならば、全単射 従って、上述した期待されるループ群の作用に関して、 本論文では、これらの予想が正しいことが示された。即ち、次の定理が証明された。 定理2. H,H’,c,c’∈Rがsign(H2+c)=sign(H’2+c’)を満たすとする。このとき、次の(i)-(iv)を満たすようなHH,cに作用する群 (i) (ii) リー群としての同型 (iii) 定理1の (iv) 上記の結果はこの方面のある意味で最終結果といえるもので、独創的な問題意識と着想のよさを込めて優れて価値のあるものである。よって論文提出者 藤岡 敦は、博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める。 | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/54538 |
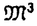 (c)を定曲率cの単連結三次元空間形とし、L(c)を
(c)を定曲率cの単連結三次元空間形とし、L(c)を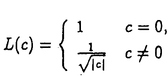
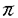 :Gc→
:Gc→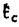
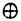 mcとすると、それに対応して、
mcとすると、それに対応して、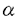 =F-1dFは
=F-1dFは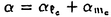 と分解される。mcはR3と同一視されるので、R3の外積×を用いて、
と分解される。mcはR3と同一視されるので、R3の外積×を用いて、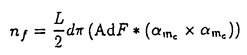
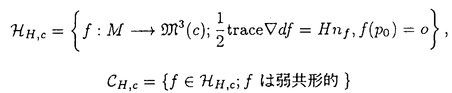
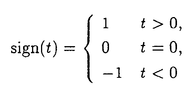
 :HH,c→HH’,c’が存在し、
:HH,c→HH’,c’が存在し、 H,c、及び、HH’,c’に作用する群
H,c、及び、HH’,c’に作用する群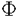 :
: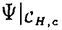 :CH,c→CH’,c’は
:CH,c→CH’,c’は