| 内容要旨 | | PART I1.はじめに 回転対称性や平行移動による不変性など,何らかの意味で対称性をもつ方程式において,解が方程式と同じ対称性をもつかどうかを調べることは,生物学や物理学への応用上も興味深いことである.無論,考察の対象をすべての解に広げると,上に述べたような「対称性の遺伝」はほとんど期待できなくなるので,解のクラスを絞り込む必要がある.本論では,安定解に対象を限定し安定性と対称性の関係について考えていく. これまでに,ある種の比較定理の成り立つ系においては,安定解への対称性の遺伝が常に起こることがわかってきている.Casten-Holland(1978),Matano(1979)は,有界領域上の半線形拡散方程式における安定平衡解への回転対称性の遺伝について論じた.その後,この結果はさらに広いクラスの方程式に対しても成り立つことがわかり,現在では,Mierczynski-Polacik(1989),Takac(1992)により強順序保存力学系のクラスに拡張され一般論にまとめられている.具体的に述べると,連結なコンパクト群の作用している強順序保存力学系においては安定解は群の作用に関して不変(すなわち対称)であることが証明されている. 本研究では,これまで知られていた結果を非コンパクト群が作用する順序保存力学系(’強’順序保存性は仮定しない)に拡張し, 安定性⇒対照性あるいはある種の単調性 という普遍的な図式が成り立つことを示す.強順序保存性の仮定を弱めることにより,退化した方程式や非有界領域上の方程式を扱うことができるようになる.その応用として,本文3節(応用例1)において,これらの方程式の安定平衡解の回転対称性を考察する.また,非コンパクト群への拡張により,群Gとして平行移動群を扱うことができるようになる.このことを用いて,(応用例2-3)において,二種競争系の進行波解および曲面の発展方程式の定常解の安定性解析に応用する. 2.主結果 Xは順序距離空間,すなわち,(閉)半順序構造(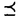 )をもつ完備距離空間とする.Xの任意の元u,vに対し,これらの最大下界u∧vが存在して,写像(u,v) )をもつ完備距離空間とする.Xの任意の元u,vに対し,これらの最大下界u∧vが存在して,写像(u,v)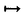 u∧v:X×X→Xは連続であると仮定する.Xの距離をdで表し,u u∧v:X×X→Xは連続であると仮定する.Xの距離をdで表し,u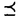 vかつu≠vをu vかつu≠vをu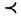 vと表す. vと表す. Tは以下の仮定(T1)-(T3)をみたすXからXへの写像とし,その半群{Tn}n=0,1,2,…を考える. (T1)順序保存性(u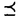 v⇒Tu v⇒Tu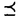 Tv). Tv). (T2)上半連続性(点列{um}m,{T(um)}mが収束するなら,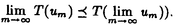 . . (T3)軌道{Tnu}n=0,1,2,…が単調減少(n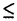 n’⇒Tnu n’⇒Tnu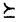 Tn’u)でかつ有界なら,相対コンパクト. Tn’u)でかつ有界なら,相対コンパクト. GはXの元に作用する連結で距離付け可能な位相群で次をみたすとする. (G1)順序保存性(u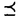 v⇒gu v⇒gu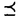 gv,∀g∈G). gv,∀g∈G). (G2)写像Tとの可換性(gTu=T(gu),∀g∈G). 定義.{T}n=0,1,2,…の平衡点 ∈Xが’下から安定’であるとは,任意の ∈Xが’下から安定’であるとは,任意の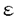 >0に対しある >0に対しある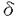 >0が存在して,d(v, >0が存在して,d(v, )< )<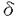 をみたす任意のv をみたす任意のv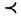  に対し,d(Tnv, に対し,d(Tnv, )< )<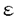 ,∀n∈Nが成り立つことをいう. ,∀n∈Nが成り立つことをいう. 以下,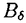 (e)はGの単位元eの (e)はGの単位元eの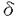 -近傍を表すものとする.次の結果を得た. -近傍を表すものとする.次の結果を得た. 主定理A.(本論Main Theorem A){Tn}n=0,1,2,…の平衡点 が,以下をみたすとする. が,以下をみたすとする. (1) は下から安定.(2){Tn}n=0,1,2,…の任意の平衡点u は下から安定.(2){Tn}n=0,1,2,…の任意の平衡点u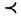  に対し,ある に対し,ある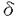 >0が存在してgu >0が存在してgu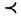  ,∀g∈ ,∀g∈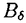 (e).このとき,g (e).このとき,g 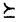  またはg またはg 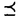  ,∀g∈Gが成り立つ. ,∀g∈Gが成り立つ. 系1.(本論Corollary 2.4) は上の定理の通りとし,さらに群Gがコンパクトであるとする.このとき, は上の定理の通りとし,さらに群Gがコンパクトであるとする.このとき, はG-不変,すなわち,g はG-不変,すなわち,g = = ,∀g∈Gが成り立つ. ,∀g∈Gが成り立つ. 系2.(本論Corollary 2.5) は上の定理の通りとし,さらにG=Rとする.このとき, は上の定理の通りとし,さらにG=Rとする.このとき, はG-不変であるか,または,g はG-不変であるか,または,g はg∈RのX値関数として狭義単調(増大または減少)である. はg∈RのX値関数として狭義単調(増大または減少)である. 注意.上で述べた定理や系は,連続力学系の場合にも,ほとんどそのままの形で成立する(本論2.2節に対応).このことに着目して,本文3節で,偏微分方程式への応用を与える.以下,連続力学系に対する結果をそれぞれ主定理B,系1’,系2’と表す. 3.応用 (応用例1.)単独の反応拡散方程式 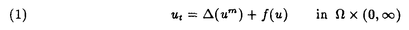 を考える.ここで, は滑らかな境界をもつRn内の有界領域とし,Dirichlet境界条件を課すものとする.また,m は滑らかな境界をもつRn内の有界領域とし,Dirichlet境界条件を課すものとする.また,m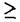 1は定数で,fはf(0)=0,f’(0)≠0をみたすC1級の関数とする.群G=回転群として系1’を適用することにより,次の定理を得る.ただし,m>1のときには,非負解のみを扱うものとする. 1は定数で,fはf(0)=0,f’(0)≠0をみたすC1級の関数とする.群G=回転群として系1’を適用することにより,次の定理を得る.ただし,m>1のときには,非負解のみを扱うものとする. 定理3.1(本論Theorem 3.1,3.3) が回転対称性をもつ領域ならば,方程式(1)の安定平衡解はすべて回転対称な関数である. が回転対称性をもつ領域ならば,方程式(1)の安定平衡解はすべて回転対称な関数である. 定理3.1は,m=1のとき,すなわち, 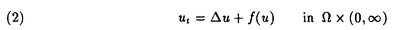 に対してはすでに知られている事実(1978 Casten-Holland,1979 Matano)であるが,それをm>1のとき(つまり,方程式(1)が退化しているとき)に拡張した結果である.また,方程式(2)において, が非有界領域である場合にも,関数fがf’(0)<0をみたせば,同様の結果―定理3.2―が成り立つ. が非有界領域である場合にも,関数fがf’(0)<0をみたせば,同様の結果―定理3.2―が成り立つ. 定理3.2(本論Theorem 3.5) が回転対称性をもつ領域ならば, が回転対称性をもつ領域ならば, 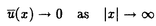 をみたす方程式(2)の安定平衡解 はすべて回転対称な関数である. はすべて回転対称な関数である. (応用例2.)二種競争系の反応拡散方程式 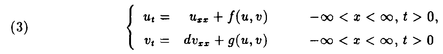 の進行波解を考える.方程式(3)が競争系とは,fv(u,v),gu(u,v)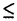 0となることをいう.方程式(3)の解(u,v)で 0となることをいう.方程式(3)の解(u,v)で 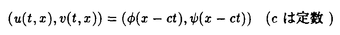 の形に表せる解を速度cの進行波解という.本論では以下の条件をみたすもののみを扱う. 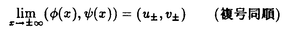 ただし,(u-,v-),(u+,v+)は常微分方程式の意味で安定な平衡解であると仮定する.関数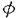 ,- ,-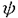 がともに単調増加(または,ともに単調減少)関数であるときに進行波解は’単調’であるという.群G=平行移動群とおくと,系2’から次が導かれる. がともに単調増加(または,ともに単調減少)関数であるときに進行波解は’単調’であるという.群G=平行移動群とおくと,系2’から次が導かれる. 定理3.3(本論Theorem 4.6)安定な進行波解は単調である. これより,孤立進行波(ソリトン)やその他単調でない進行波解はすべて不安定であることがただちにわかる. (応用例3.)Rn上の超曲面の発展方程式  を考える.ここで,nは超曲面の外向き単位法線ベクトル,Vは超曲面の外向き法線方向の速度を表す.方程式(4)は曲率に依存する超曲面の運動を一般的な形で書き表したものである.(例えば平均曲率流の場合はV=(1/(n-1))tr(∇n)と書き表される.)また,関数fは滑らかとし,方程式(4)は初期値問題として適切となるよう,強放物型であることを仮定する.群G=平行移動群とおき主定理Bを適用することにより,次を示せる. 定理3.4(本論Corollary 5.2)滑らかな定常閉曲面は不安定である. 注意.本文2節の離散力学系に対する結果を用いると,上の応用例1-3の結果を非自励系(ただし,時間tに関する周期性をもつ方程式)に拡張することができる.例えば,定理3.4は 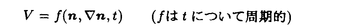 という形の方程式の周期解についても成り立つ(本論Theorem 4.1). PART II 非負正方行列の固有値の特性について述べたペロンーフロベニウスの定理を無限次元空間上の非線形写像に拡張した.具体的に述べると,順序バナッハ空間上の順序保存写像に対し分解不能性の概念を導入した上で,対応する固有値問題及びレゾルベント問題を解いた.得られた結果を用いると非線形楕円型偏微分方程式の解のさまざまな性質を調べることができる.その一例として,本論7節で,非線形楕円型方程式の解の分岐問題に対する応用を与えている. |
| 審査要旨 | | 論文提出者 荻原俊子は,群が作用している順序保存力学系における安定平衡点の対称性を,既存の理論よりもかなり広い枠組みの中で論じた.また,得られた理論を非線形偏微分方程式の解の安定性解析に応用し,新しい結果を幾つか得た. 回転対称性や平行移動による不変性など,何らかの意味で対称性をもつ方程式において,解が方程式と同じ対称性をもつかどうかを調べることは,生物学や物理学への応用上も興味深いことである.無論,考察の対象をすべての解に広げると,上に述べたような「対称性の遺伝」はほとんど期待できなくなるので,解のクラスを絞り込む必要がある.論文提出者は,安定解に対象を限定し安定性と対称性の関係について考えた. これまでに,ある種の比較定理の成り立つ系においては,安定解への対称性の遺伝が常に起こることがわかってきている.[1]Casten-Holland(1978),[2]Matano(1979)は,有界領域上の半線形拡散方程式における安定平衡解への回転対称性の遺伝について論じた.その後,この結果はさらに広いクラスの方程式に対しても成り立つことがわかり,現在では,[3]Mierczynski-Polacik(1989),[4]Takac(1992)により強順序保存力学系のクラスに拡張され一般論にまとめられている.具体的に述べると,連結なコンパクト群の作用している強順序保存力学系においては安定解は群の作用に関して不変(すなわち対称)であることが証明されている. 論文提出者は,これまで知られていた結果を非コンパクト群が作用する順序保存力学系(’強’順序保存性は仮定しない)に拡張し, 安全性⇒対称性あるいはある種の単調性 という普遍的な図式の成立を示すことに成功した.強順序保存性の仮定を弱めることにより,退化した方程式や非有界領域上の方程式を扱うことができるようになった.その応用として,論文提出者は,これらの方程式の安定平衡解の回転対称性を考察している.また,非コンパクト群への拡張により,群Gとして平行移動群を扱うことができるようになった.このことを用いて,二種競争系の安定な進行波の単調性および曲面の発展方程式の定常解の不安定性を考察している. 提出論文の内容を今少し詳しく解説しよう.Xは順序距離空間((閉)半順序構造(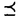 )をもつ完備距離空間)とする.Xの任意の元u,vに対し,これらの最大下界u∧vが存在することを仮定する.Xの距離をdで表し,u )をもつ完備距離空間)とする.Xの任意の元u,vに対し,これらの最大下界u∧vが存在することを仮定する.Xの距離をdで表し,u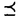 vかつu≠vをu vかつu≠vをu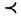 vと表す.XからXへの写像Tが生成する’力学系’,すなわち半群{Tn}n=0,1,2,…を考える.ただし,Tは順序保存性(u vと表す.XからXへの写像Tが生成する’力学系’,すなわち半群{Tn}n=0,1,2,…を考える.ただし,Tは順序保存性(u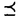 v⇒Tu v⇒Tu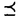 Tv)をもつ上半連続な写像で,ゆるいコンパクト性を仮定する.GはXの元に作用する連結で距離付け可能な位相群とし,その作用が順序保存性をもちTと可換であるとする.以下, Tv)をもつ上半連続な写像で,ゆるいコンパクト性を仮定する.GはXの元に作用する連結で距離付け可能な位相群とし,その作用が順序保存性をもちTと可換であるとする.以下,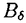 (e)はGの単位元eの (e)はGの単位元eの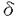 -近傍を表す.論文提出者は次の結果を得た. -近傍を表す.論文提出者は次の結果を得た. 主定理{Tn}n=0,1,2,…の平衡点 が,以下をみたすとする. が,以下をみたすとする. (i) は安定.(ii)任意の平衡点u は安定.(ii)任意の平衡点u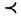  に対し,ある に対し,ある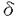 >0が存在してgu >0が存在してgu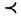  ,∀g∈ ,∀g∈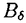 (e).このとき,g (e).このとき,g 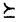  またはg またはg 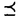  ,∀g∈Gが成り立つ. ,∀g∈Gが成り立つ. また,この主定理の系として,群Gがコンパクトであれば はG-不変(g はG-不変(g = = ,∀g∈G)であることを示している.一方,G=Rであれば ,∀g∈G)であることを示している.一方,G=Rであれば はG-不変,または,g はG-不変,または,g はg∈RのX値関数として狭義単調(増大または減少)であることを示している.さらに,これらの定理や系は,連続力学系の場合にもほとんどそのままの形で成立することも述べている. はg∈RのX値関数として狭義単調(増大または減少)であることを示している.さらに,これらの定理や系は,連続力学系の場合にもほとんどそのままの形で成立することも述べている. 論文提出者は,上で述べた一般論を,まず,単独の非線形拡散方程式 に応用した.ここで, はRn内の有界領域で,m はRn内の有界領域で,m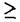 1は定数である. 1は定数である. が回転対称性をもつ領域ならば,G=回転群として前述の結果を適用することにより,方程式(1)の安定平衡解はすべて回転対称な関数であることが示される. が回転対称性をもつ領域ならば,G=回転群として前述の結果を適用することにより,方程式(1)の安定平衡解はすべて回転対称な関数であることが示される. この結果は,m=1のときに知られてた事実([1],[2])をm>1のとき(方程式(1)が退化しているとき)に拡張したものである.また,m=1のときには, が非有界領域である場合にも,同様の結果が成り立つことを論文提出者は示している. が非有界領域である場合にも,同様の結果が成り立つことを論文提出者は示している. 二種競争系の非線形拡散方程式 の進行波を考える.方程式(2)が競争系とは,fv,gu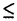 0となることをいう.方程式(2)の解(u,v)で以下の形に表せるものを進行波という. 0となることをいう.方程式(2)の解(u,v)で以下の形に表せるものを進行波という. 論文提出者は,G=平行移動群(=R)とおき前述の結果を適用し,安定な進行波は’単調’(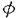 ,- ,-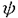 がともに単調増加,または,ともに単調減少関数)であることを証明した.これより,孤立進行波(ソリトン)やその他単調でない進行波はすべて不安定であることがただちにわかる. がともに単調増加,または,ともに単調減少関数)であることを証明した.これより,孤立進行波(ソリトン)やその他単調でない進行波はすべて不安定であることがただちにわかる. 最後に,Rn上の超曲面の発展方程式 を考える.ここで,nは超曲面の外向き単位法線ベクトル,Vは超曲面の外向き法線方向の速度を表す.方程式(3)は曲率に依存する超曲面の運動を一般的な形で書き表したものである.また,方程式(3)は初期値問題として適切となるよう,強放物型であることを仮定する.論文提出者は,G=平行移動群とおき主定理を適用することにより,滑らかな定常閉曲面の不安定性を示した. 前述の[3],[4]の理論においては,力学系が’強’順序保存性とよばれる性質をもつことは本質的であり,この仮定を弱めることは困難と思われていた.そのため,この理論の応用範囲は限られていた.論文提出者は,この強順序保存性の仮定をゆるめると同時に,他のいくつかの点においても理論を改良することに成功した.また,これまでに考えられていなかった新しい応用分野を開拓した.この点において,この方面の研究に新しい展開を与えたものとして評価できる.また,取り扱われている個々の応用例についても,順序保存力学系という新しい枠組みでこれを論じ,統一的な見地からの取扱いを可能にした点が高く評価できる. 以上の諸点を考慮した結果,論文提出者荻原俊子は,博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める. |