| 内容要旨 | | Xを代数体k上の非特異射影多様体とする。非負整数nに対し、n次のl進コホモロジーHn(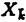 ,Ql)にはGal( ,Ql)にはGal(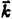 /k)が作用し、L関数L(Hn,s)が定義される。L(Hn,s)の整数点での値(特殊値)とXのdiophantine geometryとの関係は以前から興味深い研究対象であった。n=2mが偶数の時、Tate[Ta]はL関数のs=m+1での極の位数とCHm(Xk)のH2m( /k)が作用し、L関数L(Hn,s)が定義される。L(Hn,s)の整数点での値(特殊値)とXのdiophantine geometryとの関係は以前から興味深い研究対象であった。n=2mが偶数の時、Tate[Ta]はL関数のs=m+1での極の位数とCHm(Xk)のH2m(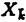 ,Ql)への像のrankとの関係を示唆した。n=1の時、BirchとSwinnerton-DyerはL関数のs=1での位数とPic0X(k)のrankは等しいという予想を出した。 ,Ql)への像のrankとの関係を示唆した。n=1の時、BirchとSwinnerton-DyerはL関数のs=1での位数とPic0X(k)のrankは等しいという予想を出した。 BlochとBeilinsonは、n=2m-1が奇数の時、独立に次の予想を出した。 予想.CHm(Xk)hom:=Ker(clm:CHm(Xk)→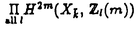 )とすると、 )とすると、 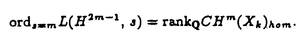 Blochは[Bl1],[Bl2]において、ords=mL(H2m-1,s)=2であるXに対し、CH2(Xk)homのnon torsionな元を構成した。この論文の主結果はこの予想の新しい例を探す試みから出たものである。主結果は、代数体上定義されたP4のある5次超曲面Vのblow up上にCH2(Vk)homの元をexplicitに与えたことである。Vは次のようなものである。(x,y)および(u,v)平面上に5本のlineのconfigurationを考える。F(x,y)=0,F’(u,v)=0を2つのconfigurationの定義方程式とする。このときF(0,0)=F’(0,0)かつ(0,0)で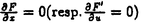 かつ かつ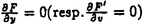 となるようとる。Vを、Affine variety F(x,y)-F’(u,v)=0のP4での閉包とする。Vはline達の交点および(0,0)から来る101個のordinary double pointをもつ。 となるようとる。Vを、Affine variety F(x,y)-F’(u,v)=0のP4での閉包とする。Vはline達の交点および(0,0)から来る101個のordinary double pointをもつ。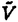 をそれらのblow upとし、Qを(0,0,0,0)上のexceptional divisorとする。QはP1×P1に同型である。 をそれらのblow upとし、Qを(0,0,0,0)上のexceptional divisorとする。QはP1×P1に同型である。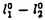 をQのrulingの差とする。主結果は、FとF’のmod.5に関するある条件の元に をQのrulingの差とする。主結果は、FとF’のmod.5に関するある条件の元に (1)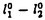 のH4( のH4(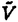 ,Z)でのコホモロジー類は10primaryである。 ,Z)でのコホモロジー類は10primaryである。 (2)cl2(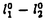 )∈H1(Gk,H3( )∈H1(Gk,H3(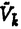 ,Z3(2)))は0でない。ここで ,Z3(2)))は0でない。ここで 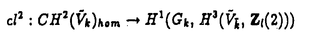 は、エタールコホモロジーのサイクル写像の理論とHochoschild-Serreのスペクトル系列を用いて定義され、arithmeticなAbel-Jacobi写像と呼ばれる。Gk=Gal(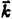 /k)である。(2)の証明にはBlochの[Bl2]での方法を用いる。その概略を述べると、Rをその商体がkであるような離散付値環とし、 /k)である。(2)の証明にはBlochの[Bl2]での方法を用いる。その概略を述べると、Rをその商体がkであるような離散付値環とし、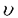 Rをそのgeneric fiberが Rをそのgeneric fiberが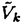 であるようなR上のregular proper modelとする。このときCH2( であるようなR上のregular proper modelとする。このときCH2(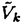 )homから )homから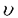 のspecial fiber のspecial fiber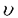 sへのspecializationであって、cl2とあるmapとの合成であるようなものを構成できる。(2)はそのspecializationによる sへのspecializationであって、cl2とあるmapとの合成であるようなものを構成できる。(2)はそのspecializationによる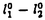 の像が非自明であることに帰着される。specializationは次のように定義される。Yを の像が非自明であることに帰着される。specializationは次のように定義される。Yを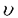 sの既約成分とする。support cohomologyのexact sequence: sの既約成分とする。support cohomologyのexact sequence: 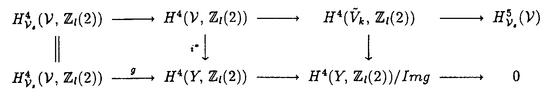 より、もし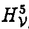 ( (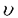 )=0ならspecialization map )=0ならspecialization map 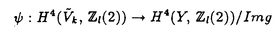 ができる。Rがstrictly henselであれば、Hochschild-Serreスペクトル系列によりspecialization 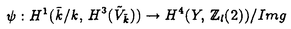 ができる。また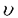 s=UDi(Diは s=UDi(Diは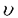 sの既約成分)とすると、specialization sの既約成分)とすると、specialization 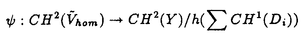 ができる。ここでhはintersectionである。この二つのspecializationの間には可換図式 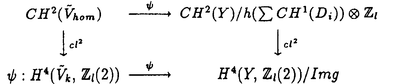 がある。cl2:CH2(Y)→H4(Y,Zl(2))が単射でImgがImhで生成されれば右のcl2は単射である。よって 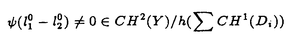 を示せば良い。 (1)については、vanishing cycleを用いた議論により、VがV0という対称性の高いvarietyである場合に帰着する。V0には5次の2面体群の直積Gが作用し、Gは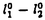 に指標 に指標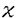 で作用する。 で作用する。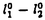 のcohomology類がtorsionであることはある方法で分かるので、次を示せば良い。 のcohomology類がtorsionであることはある方法で分かるので、次を示せば良い。 (i)H4(V0,Z[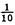 ])の ])の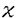 部分は代数的サイクルの類で生成される。 部分は代数的サイクルの類で生成される。 (ii)その類はtorsionでない。 (ii)はV0上のあるdivisorとの交点数を計算して示す。(i)についてはあるsmooth hyperplanesectionZ⊂V0をとり、全射 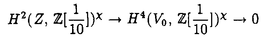 よりH2(Z,Z[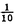 ])X=H2(Z/Ker(X),Z[ ])X=H2(Z/Ker(X),Z[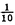 ])Xがdivisorの類で生成されることを示す。Z/Ker(X)はそのJacobianが虚数乗法をもつ種数2のcurve Cの積でdominateされることがわかる。これよりH2(Z/Ker(X),Z[ ])Xがdivisorの類で生成されることを示す。Z/Ker(X)はそのJacobianが虚数乗法をもつ種数2のcurve Cの積でdominateされることがわかる。これよりH2(Z/Ker(X),Z[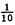 ])XがC×CのNeron-Severi群の類で生成されることがわかり、それより上のことが従う。 ])XがC×CのNeron-Severi群の類で生成されることがわかり、それより上のことが従う。 REFERENCES[Bl2]Bloch,S.,Algebraic cycles and values of L-functions I,Crelle J.(1985),379-397.[Bl1]Bloch,S.,Algebraic cycles and values of L-functions II,Duke math.J.(1985),379-397.[Ta]Tate,J.,Algebraic cycles and poles of zeta function,Arithmetical Algebraic Geometry,1965. |
| 審査要旨 | | 木村氏が博士論文で取り組んだ問題は代数多様体上の興味深い代数的サイクルの構成である。一般に多様体上に意味のある代数的サイクルを見つけることは大変難しい仕事で、数論的代数幾何における重要な問題である。ここで興味深い意味のある代数的サイクルとは代数体上定義された多様体上の代数体上定義された代数的サイクルでそのホモロジー類がゼロ(あるいはtorsion)であり、かつChow群の元としてはnon torsionであるものである。ここで重要な点は多様体や代数的サイクルが代数体という数論的な体上定義されていることである。このことにより数論への興味深い応用がなされる。この点に関してその背景となっている予想についてまず簡単に説明する。 Xを代数体上の多様体としL(Hi(X),s)をモチーフHi(X)にたいするL-関数とする。この関数はXに内在する整数論的性質を色濃く反映するもので大変重要なものである。たとえばRiemannのゼータ関数、Dedekindのゼータ関数はこの特別な場合であり、また最近話題になった志村一谷山予想は有理数体Q上の楕円曲線のL-関数が保型形式のL-関数であると主張するもので、これがフェルマーの最終定理を導く力を持っているというのがFrey-Ribetにより示されている。代数多様体のL-関数は数論の最も興味深い研究対象の一つであり、Tate予想やBirch-Swinnerton-Dyer予想といった有名な予想が現在も多くの研究者の興味を強く引きつけている。BlochとBeilinsonは後者の予想を一般化して次の予想を提出した。予想n=2m-1が奇数の時 ただしCHm(X)homはX上の余次元mの代数的サイクルの有理同値類のなすChow群の部分群でホモロジー的にゼロに同値なサイクル類からなるものとする。 この予想は一見何の関係もないように見えるXのL-関数とX上の代数的サイクルの間に神秘的なつながりがあることを示唆するもので、現在の数論幾何における最も興味深い問題の一つとなっている。特にX上のホモロジー的にゼロに同値でかつnon torsionであるような代数的サイクルの存在がXのL-関数がある整数点をゼロ点として持つこと帰結することをこの予想は示唆しているわけである。このようなサイクルの構成の一般的手続きは知られておらずBlochがm=2でords=mL(H2m-1(X),s)=2であるXにたいし構成した例の他ほとんど知られていなかった。これにたいし木村氏は今回の博士論文で新しい例を構成を試みている。主結果は、代数体上定義されたP4のある5次超局面Vのblow upにたいしCH2(V)homの元でnon zeroなものを構成したことである。具体的にはVは次のようなものである。(x,y)及び(u,v)平面上に五本のlineのconfigulationで適当な条件を満たすものを考える。F(x,y)=0とF’(u,v)=0をその定義方程式とするとき、Vをaffine variety F(x,y)-F’(u,v)=0のP4での閉包とする。適当な条件の元でVはlineたちの交点と原点(0,0,0,0)からくる101個のordinary double pointをもつ。Vをそれらのblow upとし、Qを原点上のexceptional divisorとするとQはP1×P1に同型で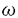 :=∈CH2( :=∈CH2(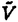 )をQのrulingの差とする。このとき主結果は )をQのrulingの差とする。このとき主結果は (1)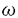 のH4( のH4(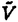 ,Z)におけるホモロジー類は10 primaryである。 ,Z)におけるホモロジー類は10 primaryである。 (2)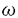 ∈CH2( ∈CH2(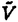 )はnon zeroである。 )はnon zeroである。 最初の主張の証明の概要は以下の通りである。まずvanishing cycleの理論を使い問題を最初に与えられた多様体よりもより扱いやすい多様体上の問題に帰着させる。その多様体は対称性をもち、それにより群の作用が存在し、これがその多様体のコホモロジー群の扱いを最初に与えられた多様体の場合よりもはるかに簡略化してくれるのである。この多様体のコホモロジー群を群作用で分解し、問題となるコホモロジー群の部分を生成する元を代数的サイクルのコホモロジー類から構成する。このために問題となっている多様体をCM型アーベル多様体をそのヤコビ多様体として持つ曲線のふたつの積と幾何的に関係づけ、これによりヤコビ多様体上の虚数乗法に対応するこの曲線上の代数的対応から求める代数的サイクルを構成する。 後半の主張の証明にはarithmeticなAbel-Jacobi写像が使われる。この写像はエタールコホモロジーの理論を用いて定義されるものでsecondaryなサイクル写像といえる。これによる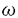 の像がnon zeroを示すのである。これはBlochにより考案されたアイデアにより示される。具体的にはVのある正標数への還元を考え、 の像がnon zeroを示すのである。これはBlochにより考案されたアイデアにより示される。具体的にはVのある正標数への還元を考え、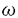 のそこへの特殊化 のそこへの特殊化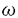 0がnon zeroを幾何的にまず証明する。次に 0がnon zeroを幾何的にまず証明する。次に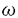 0とAbel-Jacobi写象による 0とAbel-Jacobi写象による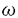 の像 の像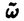 とを比較して とを比較して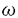 0がnon zeroであることより 0がnon zeroであることより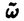 がnon zeroを示し、望むべき結果を得るのである。 がnon zeroを示し、望むべき結果を得るのである。 以上の議論は数論的、代数幾何的に高度な精緻性を持つものである。今回の結果では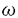 がnon zeroを示したもののnon torsionを示すまでにはいたらなかったのではあるが、以前に知られていた例は数例であったのに対し、木村氏が今回構成した例は無限個の元からなる多様体の族であり、価値の高いものであると認められる。よって、論文提出者 木村健一郎は、博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める。 がnon zeroを示したもののnon torsionを示すまでにはいたらなかったのではあるが、以前に知られていた例は数例であったのに対し、木村氏が今回構成した例は無限個の元からなる多様体の族であり、価値の高いものであると認められる。よって、論文提出者 木村健一郎は、博士(数理科学)の学位を受けるにふさわしい十分な資格があると認める。 |