| 内容要旨 | | この論文では離散的なシュレーディンガー作用素のスペクトラムに対して,大きくわけて二つの問題について論ずる. まず,第一は,あるグラフG上で定義されるラプラシアンのスペクトラムがグラフに変形を施こすとどのように変化するか,というものである.ある種のグラフ理論的な変形については具体的にその関係がわかることを示す. 第二は,一次元散乱理論に関連したある跡公式をある程度一般の離散状態空間上のマルコフ過程に対して拡張することである.さらに,その中で使う補題を用いて,物理でグッツウィラーの跡公式とよばれるものの離散版を示す. 1)Gは無限グラフ,L(G)はそのライングラフとする.ただし,L(G)はGのedgeをvertexとするグラフで,Gにおいてvertexを共有しているとき隣接しているものとする.[1]ではG上の単純酔歩が非再帰的ならばL(G)上の単純酔歩も非再帰的であることを示されている.この事実に関連してG上のラプラシアンとL(G)上のラプラシアンのスペクトラムの間にどのような関係があるか考えよう. G上のl2-空間を次の内積から定まるものとする: 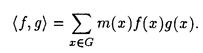 ただし,m(x)は点xにつながるedgeの本数(点xの次数)を表す. l2(G)上で次のラプラシアンのスペクトルを考える: 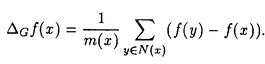 ただし,N(x)はxの近傍を表す. またGをL(G)として同様にライングラフ上でラプラシアンのスペクトルを考えることができる.Spec(- G)=Spec(G)と書くことにする. G)=Spec(G)と書くことにする. Gをd-正則グラフ(i.e.,m(x)≡d)とするとき,次の結果を得る. 定理1d 3とする.このとき, 3とする.このとき, 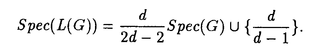 ただし,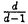 は無限多重度の固有値. は無限多重度の固有値. 同様のことは,(d1,d2)-半正則グラフについても言える.ただし,(d1,d2)-半正則グラフとは任意の辺xy∈E(G)に対してm(x)=d1,m(y)=d2またはm(x)=d2,m(y)=d1を満たすものである. 定理2Gを(d1,d2)-半正則グラフとする.また,d1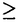 d2 d2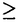 3もしくはd1>d2=2とする. 3もしくはd1>d2=2とする.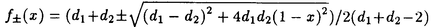 とし,さらに とし,さらに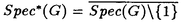 とおく.このとき, とおく.このとき, 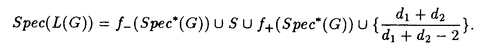 ここで,S⊂f±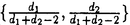 で,1が- で,1が- Gの固有値であるかないかに従って,S≠0もしくはS=0であるかが決まる. Gの固有値であるかないかに従って,S≠0もしくはS=0であるかが決まる. この定理にあらわれる集合Sを特徴づけるためにはグラフのもう少し詳しい構造が必要になる.一般にはSの可能な4通り0,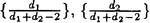 , ,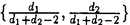 のすべての場合が起り得る. のすべての場合が起り得る. これらのスペクトラムの関係式は二つの作用素 Gと Gと L(G)との関係式から従う.例えば,定理1は次の関係式が本質的である. L(G)との関係式から従う.例えば,定理1は次の関係式が本質的である. 補題3次の関係を満たす有界線型作用素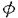 :l2(G)→l2(L(G))が存在する. :l2(G)→l2(L(G))が存在する. 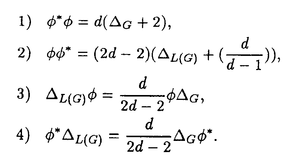 ただし,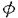 *は *は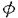 の共役作用素. の共役作用素. 上の二つの定理を証明するテクニックを用いると細分グラフ,パラライングラフと呼ばれるグラフについても同様の結果を証明することができる. 細分グラフとは元のグラフのedgeを長さが2のpathで置き換えたものである.これをS(G)と呼ぶことにすると次の定理が導かれる. 定理4Gをd-正則グラフでd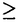 3とする.また, 3とする.また,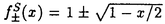 とおく.このとき, とおく.このとき, 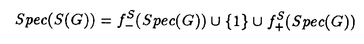 ここで,1は無限多重度の固有値. パラライングラフとは各点を完全グラフで置き換えてできるグラフであるが,これは無限グラフのある種の被覆と考えられる.これをp-L(G)と書くことにする.パラライングラフはグラフGの細分グラフのライングラフと見ることができるので,前の二つの定理2,定理4を用いるとp-L(G)のスペクトラムについて大体のことはわかる.ただし,定理2にあらわれる集合Sについては空でないことしかわからない.しかし,もう少し具体的にパラライングラフの構造を用いて解析することにより次の定理を得る. 定理5d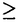 3とする.Gをd-正則グラフで,p-L(G)をそのパラライングラフとする.また, 3とする.Gをd-正則グラフで,p-L(G)をそのパラライングラフとする.また,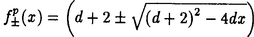 とおく.さらに, とおく.さらに,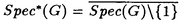 とする.このとき とする.このとき 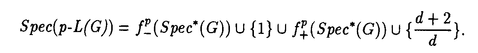 ここに1と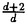 は無限多重度の固有値. は無限多重度の固有値. また,これらの定理を応用すると,いくらでも多くのgapを持つグラフを構成することができる. 2)L=- G+Vというシュレーディンガー作用素と一点 G+Vというシュレーディンガー作用素と一点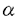 でディリクレ条件を課した作用素 でディリクレ条件を課した作用素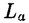 の差のトレースについて,特にVが周期ポテンシャルのとき の差のトレースについて,特にVが周期ポテンシャルのとき 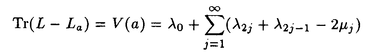 という関係式が得られるが,これはHill’s theoryでよく知られている等式である.Craigは[3]でこの結果を周期ポテンシャルを含むreflectionlessとよばれるポテンシャルのクラスに拡張し,Simon等は[4]でスペクトラムのシフトをあらわす散乱量を用いて,関連する結果を統一的に扱った.これらの結果はいずれもR1上の作用素Lに対する結果であるが,これを可算集合上の離散的シュレーディンガー作用素Lと有限集合A上でディリクレ条件を置いた作用素LAに対して拡張する. Gは可算無限集合とし,P={p(x,y)}x,y∈Gを推移確率とする.ただし,Pとしてはsupx∈G|{r∈G;p(x,r)>0}|<∞を満たすものを考えることにする.以下,Gの有限部分集合Aを固定し,Vは実数値有界関数とする.l2(G)上のラプラシアンを 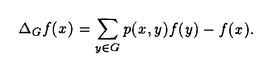 で定義し,シュレーディンガー作用素L=- G+Vに対して次の二つの問題を考える. G+Vに対して次の二つの問題を考える. 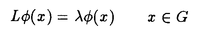 と 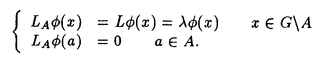 ただし,これら二つの作用素の定義域はそれぞれD(L)=l2(G),D(LA)={f∈l2(G);f(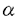 )=0∀a∈A}とする.この作用素に対するレゾルベント(L- )=0∀a∈A}とする.この作用素に対するレゾルベント(L- )-1,(LA- )-1,(LA- )-1の積分核(グリーン関数)を )-1の積分核(グリーン関数)を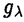 (x,y), (x,y),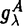 (x,y)とする.また,L,LAに対応する熱方程式の基本解をそれぞれ,pV(t,x,y),pVA(t,x,y)とおく.さて,ここで (x,y)とする.また,L,LAに対応する熱方程式の基本解をそれぞれ,pV(t,x,y),pVA(t,x,y)とおく.さて,ここで ∈Rに対して ∈Rに対して 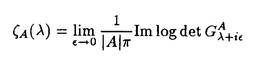 と定義する.ただし,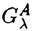 は|A|×|A|行列で成分が( は|A|×|A|行列で成分が(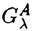 )a,b= )a,b=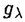 (a,b)なるものである.この量 (a,b)なるものである.この量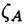 ( ( )はa.e. )はa.e. ∈Rで存在する.このとき,次の定理を示すことができる. ∈Rで存在する.このとき,次の定理を示すことができる. 定理6Vを実数値有界関数とする.このとき, 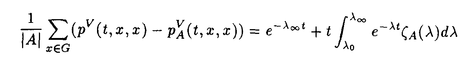 ただし, 0, 0, ∞はそれぞれLのスペクトラムの下限と上限. ∞はそれぞれLのスペクトラムの下限と上限. さらに,上定理の左辺のt→0での漸近挙動を調べることにより,次の系を得る. 系7Vを実数値有界関数とする.このとき, 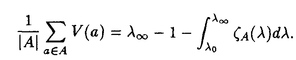 また, 0, 0, ∞はそれぞれ作用素Lのスペクトラムの下限と上限である. ∞はそれぞれ作用素Lのスペクトラムの下限と上限である. この系はポテンシャルやグラフが特別な場合には更にきれいな形で書くことができる.例えば,GをZ1,Vを周期関数とする.有限集合Aは一点{a}にとる.このとき,Lのスペクトラムは一般に有限個の閉区間の和集合になることが知られている.それを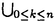 [ [ 2k, 2k, 2k+1]とする.ただし, 2k+1]とする.ただし, 2n+1= 2n+1= ∞.また,グリーン関数 ∞.また,グリーン関数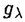 (a,a)はレゾルベント集合( (a,a)はレゾルベント集合( 2k-1, 2k-1, 2k)上狭義単調増加だからその零点は高々一つで,それを 2k)上狭義単調増加だからその零点は高々一つで,それを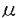 kとする.もし,零点がない場合はその正負に従って kとする.もし,零点がない場合はその正負に従って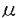 k= k= 2k-1, 2k-1,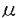 k= k= 2kとする.このとき, 2kとする.このとき, 定理8Vを実数値有界関数とする.このとき, 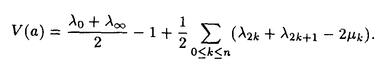 これは始めに述べた関係の離散アナロジーである. さて,これらの定理の証明の際に用いた補題で次のようなものがある. 補題9 ∈C\[ ∈C\[ 0, 0, ∞]とする.このとき, ∞]とする.このとき, 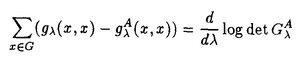 上式の右辺を展開するためにG×G上の関数として 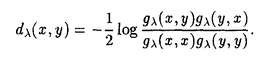 を考える.これは,G上の距離となる.このとき, 定理10ある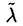 ∈Rが存在して, ∈Rが存在して, < <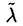 のとき,次のような展開がある. のとき,次のような展開がある. 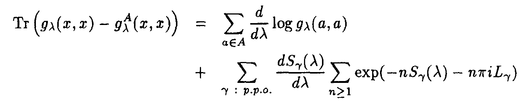 ただし,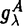 (x,x)は(LA- (x,x)は(LA- )に対するグリーン関数, )に対するグリーン関数,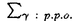 は有限集合A上の素な周期軌道に対する和, は有限集合A上の素な周期軌道に対する和,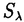 ( (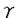 )はG上の距離 )はG上の距離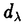 で測った で測った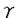 の長さ, の長さ,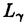 ∈Nは ∈Nは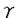 の周期. の周期. 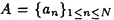 とおく.このとき, とおく.このとき,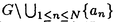 を を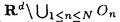 (ただし,Onは有界領域)を離散化したものであると見なすと,物理の分野でグッツウィラー跡公式と呼ばれる関係の一つの離散アナロジーと見ることができる. (ただし,Onは有界領域)を離散化したものであると見なすと,物理の分野でグッツウィラー跡公式と呼ばれる関係の一つの離散アナロジーと見ることができる. References[1]Y.Higuchi.Isoperimetric inequality and random walks on an infinite graph and its line graphs.in preparation.[2]B.Mohar and W.Woess.A survey of spectra of infinite graphs.Bull.London Math.Soc.21(1989),209-234.[3]W.Craig.The Trace Formula for Schrodinger Operators on the Line.Commun.Math Phys.126(1989),379-407.[4]F.Gesztesy,H.Holden,B.Simon.Absolute Summability of the Trace Relation for Certain Schrodinger Operators.Commun.Math Phys.168(1995),137-161.[5]M.C.Gutzwiller.Chaos in Classical and Quantum Mechanics.Springer Verlag,Berlin,1990. |