| 内容要旨 | | ★この論文では量子グラスマン多様体(G/K)q(real,symplectic)上の球関数がトーラス T={x=(x1,…,x1)∈(Cl)l;|x1|=…=|x1|=1} 上で次の(Cl)l上の有理関数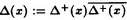 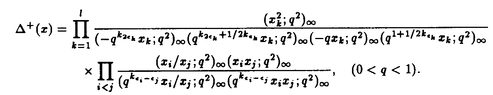 を重み関数とするT上の不変ハール測度に関するワイル群不変な直交多項式系として特徴付けられることを示した。ただし、上で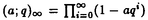 で{ で{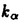 }は対称空間であるG/Kの制限ルート系 }は対称空間であるG/Kの制限ルート系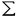 のルート のルート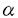 の重複度に対応している。特にここに現われるq-直交多項式はp進体上の球関数の研究から出てきたいわゆるMacdonald多項式([M]) または Koornwinderの多変数版Askey-Wilson多項式([K2])と呼ばれるものと一致する。(定理 4.1) の重複度に対応している。特にここに現われるq-直交多項式はp進体上の球関数の研究から出てきたいわゆるMacdonald多項式([M]) または Koornwinderの多変数版Askey-Wilson多項式([K2])と呼ばれるものと一致する。(定理 4.1) 上にあげた量子グラスマン多様体とは次に示す制限ルート系をもつ対称空間のq-deformationである。(oの上の数字がルートの重複度) 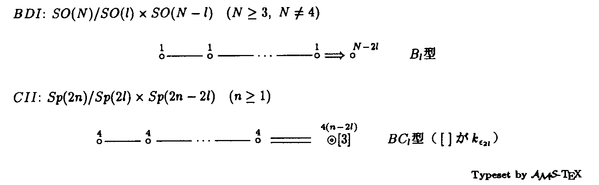 この論文といままでの結果[N](野海),[NS1],[NS2](野海-杉谷)をあわせると古典型既約リーマン対称空間のあるq-deformation上の帯球関数は上のパラメトライゼイションで統一的に表わせることも得られた。(複素グラスマン多様体のときは少しだけ異なる。([NDS])) ★一般に対称空間G/K(ここでは、古典型コンパクト対称対(G,K))のq-deformationである量子対称空間(G/K)qは量子群、即ちここでは’量子包絡環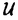 =Uq(g)’とGの有理表現に関する有限次元integrable表現の行列成分で張られる =Uq(g)’とGの有理表現に関する有限次元integrable表現の行列成分で張られる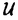 の双対Objectの1つである’量子座標関数環A=Aq(G)’の枠組みにおいて導入されたG/K上の量子座標関数環Aq(G/K)において指定されるobjectと認識されるものである。 の双対Objectの1つである’量子座標関数環A=Aq(G)’の枠組みにおいて導入されたG/K上の量子座標関数環Aq(G/K)において指定されるobjectと認識されるものである。 量子群初期の頃は階数1(1変数)のq-直交多項式達が量子座標環Aの余加群表現の行列要素として、自然に現われた。([VS],[MMNNU],[K1]) これらは全て離散測度(q-integral)に関する直交多項式系であったので一般の場合でも量子群における球関数はこのような離散測度に関する直交関数系であると思われていた。しかし、現在の立場から見直すと、量子対称空間上の球関数についていえば、GCとKCがルート系の埋め込みに自然に対応している場合、量子群でいえばA=Aq(G)からAq(K)への自然な全射ホップ代数射が存在する場合が、離散測度に関するq-直交関数系を生み出す構図になっている。もちろんこのような例は限られた場合であるし高階の自然な例である量子複素グラスマン多様体(U(n)/U(l)xU(n-l))qの定義は容易だが、球関数は後述のヘッケ環H=Aq(K\G/K)の構造が見にくいため、上のような方法では階数1の場合を除いて進展しなかった。しかし、その後Koornwinderの仕事[K1]をはじめとして [NM],[UT],[N],[S],[NS1,2]によってUの中に"infinitesimal subgroup"と我々が呼ぶ’余イデアル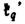 を構成することによって"部分群"の自由度を回復した。特に高階数の量子対称空間については、野海[N]によるAl型の場合を皮切りに、野海-杉谷[NS1,2]により古典型既約リーマン対称空間と呼ばれる系列全てについて、R-行列、L-作用素に関する反射関係式(制限つきヤン・バクスター方程式)の解(Cartan involutionに関係する)を発見することによって統一的な構成を与えた。 を構成することによって"部分群"の自由度を回復した。特に高階数の量子対称空間については、野海[N]によるAl型の場合を皮切りに、野海-杉谷[NS1,2]により古典型既約リーマン対称空間と呼ばれる系列全てについて、R-行列、L-作用素に関する反射関係式(制限つきヤン・バクスター方程式)の解(Cartan involutionに関係する)を発見することによって統一的な構成を与えた。 ★(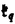 , ,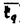 )-不変部分環 )-不変部分環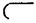 はある はある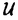 のinvolutive反代数射)であるヘッケ環H=Aq(K\G/K)(可換環になる!)の球表現に対応する各成分のベクトルを帯球関数と呼ぶ。 のinvolutive反代数射)であるヘッケ環H=Aq(K\G/K)(可換環になる!)の球表現に対応する各成分のベクトルを帯球関数と呼ぶ。 これを特徴付けるために、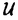 のカシミールに相当するある中心元Cの動径成分を決定することが大きな役割を果たす。即ち、Gのトーラスに相当するAの可換部分ホップ代数 のカシミールに相当するある中心元Cの動径成分を決定することが大きな役割を果たす。即ち、Gのトーラスに相当するAの可換部分ホップ代数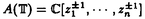 への(単射)制限像H|Tの上でのCの作用の部分をq-差分作用素によって表示することが可能である。実際に互いにdual objectであるホップ代数A, への(単射)制限像H|Tの上でのCの作用の部分をq-差分作用素によって表示することが可能である。実際に互いにdual objectであるホップ代数A,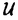 からくる双対性H→ からくる双対性H→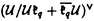 (単射埋込)により、この動径成分を計算することができ、帯球関数 (単射埋込)により、この動径成分を計算することができ、帯球関数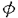 |Tは次のHeckman-Opdam型ワイル群不変q-差分作用素の同時固有関数として得られる。 |Tは次のHeckman-Opdam型ワイル群不変q-差分作用素の同時固有関数として得られる。 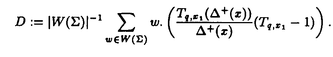 [NS1,2]では、上のリーマン対称空間のほとんどを占めるグラスマン多様体の系列における球関数は、制限ルート系のルートの重複度の高さと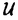 -加群代数の0-weighted subspaceの複雑さからくる困難によって決定されていない。この論文ではそれらを克服して、古典型リーマン対称空間に付随する量子対称空間上の球関数をはじめに与えた統一的な表示で特徴付けた。 -加群代数の0-weighted subspaceの複雑さからくる困難によって決定されていない。この論文ではそれらを克服して、古典型リーマン対称空間に付随する量子対称空間上の球関数をはじめに与えた統一的な表示で特徴付けた。 REFERENCES[K1] Koornwinder,T.H.,Continuous q-Legendre polynomials as spherical matrix elements of irreducible representations of the quantum SU(2)group,CWI Quarterly 2(1989),171-173.[K2] _,Askey-Wilson polynomials associated with root systems of type BC,Comtemp.Math.138(1992),189-204.[M] Macdonald,I.G.,Orthogonal polynomials associated with root systems,Oxford preprint(1988).[MMNNU] Masuda,T.,Mimachi,K.,Nakagami,Y.,Noumi,M.and Ueno,K.,Representations of quantum group SUq(2)and the little q-Jacobi polynomials,J.Func.Anal.99(1991),357-386.[N] Noumi,M.,Macdonald’s symmetric polynomials as zonal spherical functions on some quantum homogeneous spaces,Adv.in Math.(to appear).[NM] _,Askey-Wilson polynomials and the quantum group SUq(2),Proc.Japan Acad.66(1990),146-149.[NS1] _,Quantum symmetric spaces and related q-orthogonal polynomials,in:"Group Theoretical Methods in Physics",Proceedings XXICGTMP,Toyonaka(Japan),1994,ed.A.Arima et al.,World Scientific,Singapore,1995,pp.28-40.[NS2] _,Quantum symmetric spaces and multivariable q-orthogonal polynomials,preprint.[S] Sugitani T.,Harmonic analysis on quantum spheres associated with representations of Uq(SON)and q-Jacobi polynomials,Composito Math.99(1995),249-281.[UT] Ueno,K.and Takebayashi,T.,Zonal spherical functions on quantum symmetric spaces and Macdonald’s symmetric polynomials,in"Quantum Groups"(P.P.Kulish,ed.),Proceedings of Workshops held in the International Mathematical Institute,Leningrad.Fall 1990,Lecture Notes in Math.,vol.1510,Springer-Verlag,1992,pp.142-147.[VS] Vaksman,L.L.and Soibelman,Ya.S.,Algebra of functions on the quantum group SU(2),Func.Anal.Appl.22(1988),170-181. |
| 審査要旨 | | 「量子群」は1980年代以降の純粋数学と数理物理との相互作用において、中心的な役割を果たしている概念の一つであり、対称性を記述する新しい構造として、数学の内部にも様々な影響を与えてきた。量子群(あるいは量子環)は、Lie群やLie環をHopf代数の水準で変形したものであり、qと書かれる変形のパラメータを含む。このような枠組みの中で、Lie理論と、それに関連する幾何学的あるいは解析的な理論の類似を、どの程度まで展開できるか という問題は、数学的にも興味深い問題であり、多くの研究者の関心を集めてきた。 量子群上の調和解析は、そのような問題の一つである。87年から88年にかけて、最も基本的な量子群である2次の量子ユニタリ群SUq(2)について、その既約ユニタリ表現の行列要素が、Jacobi多項式のq類似の一つで表示されることが発見され、それを契機に量子群と「q解析」の直接の結びつきが顕在化することとなった。その後90年頃までの間に、Podlesの量子球面に関連して、Askey-Wilson多項式に至る種々のq-Jacobi多項式が量子群の等質空間の球函数として実現され、古典的な1変数q直交多項式の群論的な根拠が明らかにされた。 球函数論の立場から言えば、これらは本質的に階数1の対称空間の場合である。実Rieman対称空間の帯球函数(の動径成分)は、制限ルート系とルートの重複度によってきまるHarish-Chandraの微分方程式の解であり、対称空間がコンパクトな場合には、これらはトーラス上の多変数の直交多項式系を定める。I.G.Macdonaldは、同じく88年前後に、このような多変数直交多項式のq類似として、ルート系に付随する多変数のq直交多項式、いわゆる「Macdonald多項式」を導入し、様々な組合せ論的な問題との関連を指摘した。これは、有限体やp進体上の古典群の球函数を特殊な場合に含むような多変数特殊函数のクラスであり、qの世界の新しい対象である量子群との関係が問題上なるのは、自然な流れであった。 量子群の枠組みで、高階数の対称空間(以下ではコンパクトな実形の言葉でのべる)の対応物を具体的に考察した最初の例は、上野喜三雄・竹林忠吉によるSU(n)/SO(n)の場合である(90年)。彼等はn=3の場合、即ち量子対称空間(SU(3)/SO(3))qの帯球函数がA2型Macdonald多項式の実現を与えることを示し、一般のnの場合は帯球函数がAn-1型Macdonald多項式で与えられるであろうと予想したが、量子群の座標環や量子包絡環の定義関係式の複雑さのため、彼等の直接的な方法を一般の階数で遂行するのは困難であった。その後野海正俊はSU(n)/SO(n),SU(2n)/Sp(2n)に対応する量子対称空間を、いわゆるR行列とL作用素の言葉で定式化し、その帯球函数がAn-1型Macdonald多項式の実現を与えることを確立した(92年)。そこで用いられたのは、反射方程式(境界型Yang-Baxter方程式)の定数解を用いて、量子環のコイデアルを構成し、量子包絡環の言葉だけでCasimir元の動径成分を決定する方法である。 論文提出者杉谷哲也が、量子群の調和解析に関連した研究を開始したのは、このような時期であった。提出論文に先立ち、杉谷は量子群S0q(n)上の量子球面を考察し、そこでの球面調和函数の理論を構成している(修士論文)。その後提出論文まで、高階数の古典型量子対称空間とその球函数論の系統的な研究を精力的に行い、この分野の最も重要な研究者の一人として、国際的にも既に高い評価を得ている。 古典型Riemann対称空間(コンパクト形)G/Kには次の10個の系列がある。 (1)の場合の帯球函数は表現の指標であり、これはq変形を受けない。(2)が野海の考察したA型の場合である。杉谷は、(3),(4)の場合に対応する反射方程式の定数解を構成し、それによって定義される量子包絡環のコイデアル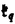 を用いて、量子群の座標環Aq(G)の を用いて、量子群の座標環Aq(G)の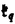 -不変式環Aq(G/K)をとるというやり方で、これらの系列の統一的な「量子化」を行った(94年、野海との共同研究)。この枠組みでは、Aq(G)の両側 -不変式環Aq(G/K)をとるというやり方で、これらの系列の統一的な「量子化」を行った(94年、野海との共同研究)。この枠組みでは、Aq(G)の両側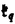 不変な元で、量子包絡環の中心の同時固有「函数」となるものが、量子対称空間(G/K)qの帯球函数である。この共同研究において、杉谷は(3)の系列に対して、帯球函数が制限ルート系に対応するMacdonald多項式か、BC型の場合にはMacdonald多項式の拡張である、Koornwinderによる多変数Askey-Wilson多項式によって記述されることを示している。(4)のうちSU系列のGrassmann多様体については、野海,M.Dijkhuizenとの共同研究で、新しい変形族へ拡張した形で、帯球函数を決定している。 不変な元で、量子包絡環の中心の同時固有「函数」となるものが、量子対称空間(G/K)qの帯球函数である。この共同研究において、杉谷は(3)の系列に対して、帯球函数が制限ルート系に対応するMacdonald多項式か、BC型の場合にはMacdonald多項式の拡張である、Koornwinderによる多変数Askey-Wilson多項式によって記述されることを示している。(4)のうちSU系列のGrassmann多様体については、野海,M.Dijkhuizenとの共同研究で、新しい変形族へ拡張した形で、帯球函数を決定している。 量子対称空間の球函数論においても、量子包絡環の中心元の動径成分を決定することが最も本質的なステップとなる。これは、古典的なHarish-Chandraの方法の量子群版にあたる部分である。上述の(4)のGrassmann多様体の3つの系列では、反射方程式の定数解が複雑なため、中心元の動径成分の計算を実際に実行するのは極めて困難であり、上述の共同研究ではこの系列の帯球函数を決定することができていなかった。動径成分の分析を精密に行うことによりこの困難を克服し、SOおよびSpの系列の量子Grassmann多様体について、量子包絡環の中心元の動径成分を決定し、その帯球函数がMacdonald多項式および多変数Askey-Wilson多項式で記述されることを示したのが、この提出論文の内容である。この杉谷の研究によって、古典型Riemann対称空間のすべてについて、量子群の枠組みでの一つの標準的な構成と、その帯球函数の決定という基本的な問題が完成したことになる。 以上に見るように、論文提出者杉谷哲也は古典型量子対称空間の球函数論に関して本質的な貢献をなし、提出論文によってこの基本課題を完成させた。その研究は、有限体、p進体、実数体上の理論との対比においても重要な業績であり、今後も表現論と特殊函数論の発展にとって大きな役割を演じうるものと期待される。よって論文提出者杉谷哲也は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |