| 内容要旨 | | まず、このテーマの背景にある予想(Greenberg予想)について説明する。kを有理数体Q上の有限次拡大体、pを素数、k∞をkの円分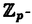 拡大とする。このとき、k∞/kの中間体のイデアル類群のp-partの増大度を表す不変量 拡大とする。このとき、k∞/kの中間体のイデアル類群のp-partの増大度を表す不変量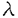 p(k), p(k),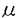 p(k)が定まる。問題とする予想は、「kが総実であるならば、全ての素数pに対して、 p(k)が定まる。問題とする予想は、「kが総実であるならば、全ての素数pに対して、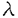 p(k)= p(k)=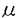 p(k)=0となるであろう」というものである。この予想は、1973年[I]において岩澤氏により問題として挙げられ、更に、Greenberg氏[G]やCandiotti氏[C]らにより、各k,pに対する予想の必要十分条件が与えられ、実際に予想が成立する自明でない例が示された。その後、幾人かの研究者により予想の判定条件が与えられ、それらに対する数値計算等も行われているが、一般的な結果は得られていない。この点では任意のQ上のアーベル拡大と素数pに対し成立することが知られているLeopoldt予想([B])や p(k)=0となるであろう」というものである。この予想は、1973年[I]において岩澤氏により問題として挙げられ、更に、Greenberg氏[G]やCandiotti氏[C]らにより、各k,pに対する予想の必要十分条件が与えられ、実際に予想が成立する自明でない例が示された。その後、幾人かの研究者により予想の判定条件が与えられ、それらに対する数値計算等も行われているが、一般的な結果は得られていない。この点では任意のQ上のアーベル拡大と素数pに対し成立することが知られているLeopoldt予想([B])や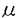 p(k)=0の予想([FW])とは、状況が大きく異なっている。 p(k)=0の予想([FW])とは、状況が大きく異なっている。 本論文では、ある種のQ上の実アーベル体に対する予想の必要十分条件を円単数、p進L関数、更にある条件を満たす素数達を用いて、簡明な形で与えた。この条件は、Vandiver予想(p-分体の最大総実部分体の類数はpで割れない)の古典的な判定条件の一般化になっており、各k,pに対する予想が成立するかどうかを確かめる上でも有効である。実際、p=3,k=Q(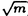 )(1<m<104,m:square free)の範囲では予想がすべて成立していることをコンピューターによる数値計算で確認した。この内多くのものは、これまでの調査によって予想の成立が確かめられており、今回の数値計算により新しく確認された例は、いずれも判定条件で高次の体の単数を扱う必要がある「面倒な」ものたちである。この中には、1970年代にGreenberg氏、Candiotti氏らが、予想の成立が不明であるとして挙げていたQ( )(1<m<104,m:square free)の範囲では予想がすべて成立していることをコンピューターによる数値計算で確認した。この内多くのものは、これまでの調査によって予想の成立が確かめられており、今回の数値計算により新しく確認された例は、いずれも判定条件で高次の体の単数を扱う必要がある「面倒な」ものたちである。この中には、1970年代にGreenberg氏、Candiotti氏らが、予想の成立が不明であるとして挙げていたQ(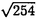 ),Q( ),Q(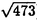 )の2つの「悪名高い」例も含まれており、興味深い。なお、同時期にKraft氏とSchoof氏[KS]により、p=3,pが分解しない実2次体に対して、異なった方法で同様な数値計算がなされたが、上の2例を含む数例に計算ミスがあることを福田氏、小松氏、栗原氏、田谷氏らと共に指摘した。 )の2つの「悪名高い」例も含まれており、興味深い。なお、同時期にKraft氏とSchoof氏[KS]により、p=3,pが分解しない実2次体に対して、異なった方法で同様な数値計算がなされたが、上の2例を含む数例に計算ミスがあることを福田氏、小松氏、栗原氏、田谷氏らと共に指摘した。 本論文は2つのChapterからなり、それぞれの主な内容は次の通りである。 Chapter1 (I)条件(C1)(C2)(C3)(後述)のもとでのGreenberg予想の判定条件。 (II)イデアルの単項化と判定条件との関係。 (III)p=3(resp.5,7)、(C1)(C2)(C3)を満たすQ(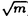 ),1<m<104(resp.2*104,3*104)に対する判定条件の適用。 ),1<m<104(resp.2*104,3*104)に対する判定条件の適用。 Chapter2 (I)Greenberg予想に対する判定条件((C1)(C2)(C3)を仮定しない)。 (II)岩澤多項式の近似式の計算方法。 (III)p=3、Q(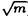 ),1<m<104に対する判定条件の適用。 ),1<m<104に対する判定条件の適用。 以下、本論文の主結果であるGreenberg予想の判定条件(Chapter2)について説明する。k/Q:実アーベル体、p:奇素数、kn:k∞/kのn番目の中間体、An:knのイデアル類群のp-part、A∞=limAn(射影極限はノルム写像による)とする。技術的な理由(有理整数内の計算で済ませられる)により、次の仮定をする。 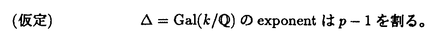  -分解によって、pとkに対するGreenberg予想をより精密に調べることにする。Xを -分解によって、pとkに対するGreenberg予想をより精密に調べることにする。Xを の1次の指標とすると、仮定によりp進体 の1次の指標とすると、仮定によりp進体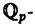 値と見なすことができる。eX∈Zp[ 値と見なすことができる。eX∈Zp[ ]をXの巾等元とし、A∞(X)=eXA∞とおく。fXをXのconductor、q=l.c.m(fX,p)、 ]をXの巾等元とし、A∞(X)=eXA∞とおく。fXをXのconductor、q=l.c.m(fX,p)、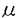 pを1のp乗根のなす群とし、 pを1のp乗根のなす群とし、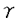 0をGal(k∞( 0をGal(k∞(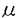 p)/k( p)/k(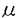 p))の位相生成元で、任意の1のpn乗根 p))の位相生成元で、任意の1のpn乗根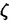 に対し に対し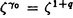 となるものとする。A∞(X) となるものとする。A∞(X)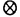 Qpは、Qp上有限次線形空間になることが知られている。そこでchar A∞(X)により、A∞(X) Qpは、Qp上有限次線形空間になることが知られている。そこでchar A∞(X)により、A∞(X)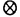 QpにおけるT= QpにおけるT=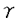 0-1の作用に対する特性多項式を表し、 0-1の作用に対する特性多項式を表し、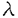 Xをchar A∞(X)の次数とする。(p,X)に対するGreenberg予想とは、Ferrero-Washingtonの定理から次を意味する。 Xをchar A∞(X)の次数とする。(p,X)に対するGreenberg予想とは、Ferrero-Washingtonの定理から次を意味する。 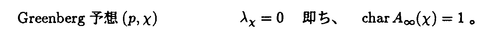 この予想を次の3つの場合に分けて考える。(A)X(p)≠1かつX-1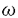 (p)≠1、(B)X-1 (p)≠1、(B)X-1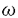 (p)=1、(C)X(p)=1。この場合分けは、それぞれ局所単数群の構造が異なっていることによる。 (p)=1、(C)X(p)=1。この場合分けは、それぞれ局所単数群の構造が異なっていることによる。  X、char A∞(X)には、Mazur-Wilesにより証明された岩澤主予想から得られる上界が存在する。以下、その上界を説明する。gX(T)をp進L関数Lp(s,X)に対応する形式的巾級数(gX((1+q)1-s-1)=Lp(s,X))とする。Ferrero-Washingtonの定理とp進Weierstrass準備定理から、gX(T)=PX(T)uX(T)(PX(T):distinguished polynomial,uX(T):Zp[[T]]の単数)と一意的に書ける。(B)の場合、Lp(s,X)は自明な零点を持つため、T-qはPX(T)を割る。そこで、(A)(C)の場合、PX(T)=PX(T)、(B)の場合、PX(T)=PX(T)/(T-q)とおく。Mazur-Wilesの定理(と因子T-qに関する議論((B)の場合))から、次の上界が得られる。 X、char A∞(X)には、Mazur-Wilesにより証明された岩澤主予想から得られる上界が存在する。以下、その上界を説明する。gX(T)をp進L関数Lp(s,X)に対応する形式的巾級数(gX((1+q)1-s-1)=Lp(s,X))とする。Ferrero-Washingtonの定理とp進Weierstrass準備定理から、gX(T)=PX(T)uX(T)(PX(T):distinguished polynomial,uX(T):Zp[[T]]の単数)と一意的に書ける。(B)の場合、Lp(s,X)は自明な零点を持つため、T-qはPX(T)を割る。そこで、(A)(C)の場合、PX(T)=PX(T)、(B)の場合、PX(T)=PX(T)/(T-q)とおく。Mazur-Wilesの定理(と因子T-qに関する議論((B)の場合))から、次の上界が得られる。 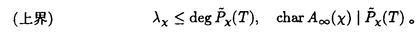 ここで、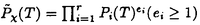 と素因子分解し、各i、nに対して、自然数 と素因子分解し、各i、nに対して、自然数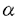 i,n、多項式Yi,n(T)∈Z[T]、円単数ci,nを以下のように定義する。(kn,pに対するLeopoldt予想が成立することから、ai,n<∞となる。) i,n、多項式Yi,n(T)∈Z[T]、円単数ci,nを以下のように定義する。(kn,pに対するLeopoldt予想が成立することから、ai,n<∞となる。) 定義1.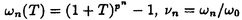 とおく。 とおく。 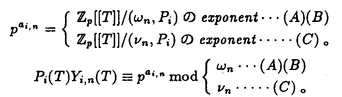 定義2.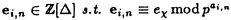 かつ係数和が零。fn:knのconductor、 かつ係数和が零。fn:knのconductor、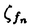 2:1の原始fn乗根、t:p上のkの素イデアルによる剰余体の位数とおく。 2:1の原始fn乗根、t:p上のkの素イデアルによる剰余体の位数とおく。 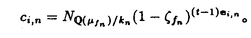 定理.記号および設定は、以上の通りとする。 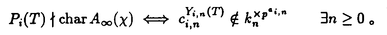 特に全てのiで右辺が成立すれば、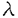 X=0である。 X=0である。 系. 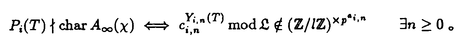 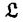 は は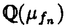 の1次の素イデアル、l= の1次の素イデアル、l=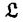 ∩Q。 ∩Q。 円単数ci,n,多項式Yi,n(T),自然数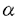 i,nは、実際に計算可能な明確な元であることに注意する。そのため系の右辺は、素数l(fnを法として1と合同)と有限体Flの原始根を求めることにより各lごとに整数計算でその正否を確かめられる有効な判定条件となっている。なお、これまでに与えられていた判定条件の多くは、主にknの単数群を用いて記述されており、高次の体の単数群を扱う必要がある場合(即ちnが大きいとき)その条件を確かめるのは困難であった。 i,nは、実際に計算可能な明確な元であることに注意する。そのため系の右辺は、素数l(fnを法として1と合同)と有限体Flの原始根を求めることにより各lごとに整数計算でその正否を確かめられる有効な判定条件となっている。なお、これまでに与えられていた判定条件の多くは、主にknの単数群を用いて記述されており、高次の体の単数群を扱う必要がある場合(即ちnが大きいとき)その条件を確かめるのは困難であった。 最後に、Chapter1,Chapter2,参考論文[IS]における市村氏、私の寄与について説明する。先に述べた判定条件の原型は、ガウス和の研究および整数環の研究から派生したアイデアを用いて、市村氏により以下の条件(C1)(C2)(C3)のもとで与えられた(Chapter1)。(C1)kにおけるp上の素イデアルは1つのみ,(C2)X-1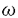 (p)≠1,(C3)deg PX(T)=1。 (p)≠1,(C3)deg PX(T)=1。 私は、実例としてp=3,5,7,判別式の小さい実2次体たち(p=3,Q(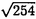 ),Q( ),Q(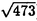 )の2例を含む)に対して判定条件を適用して予想の成立を確かめ、この判定条件の有効性を明らかにした。なおp=5,7での数値計算は、高次の体の単数群を扱うことが困難であるため、これまでほとんど実行されていなかった。 )の2例を含む)に対して判定条件を適用して予想の成立を確かめ、この判定条件の有効性を明らかにした。なおp=5,7での数値計算は、高次の体の単数群を扱うことが困難であるため、これまでほとんど実行されていなかった。 次に私は、(C1)(C2)を仮定しない予想の判定条件を、(A)X-1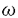 (p)≠1かつX(p)≠1,(B)X-1 (p)≠1かつX(p)≠1,(B)X-1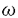 (p)=1,(C)X(p)=1の3つの場合に分けて与えた。(B),(C)の場合、局所単数群の構造がChapter1で扱ったものとは異なるため、判定条件もそれに応じて異なった形をとることになる。 (p)=1,(C)X(p)=1の3つの場合に分けて与えた。(B),(C)の場合、局所単数群の構造がChapter1で扱ったものとは異なるため、判定条件もそれに応じて異なった形をとることになる。 一方、市村氏は、Chapter1とは異なった議論([IS])を用いて、p-分体に対して(C3)の代わりにPX(T)の零点の有理性を仮定した予想の判定条件を与えた。この条件は、円単数とPX(T)の零点達を用いてChapter1の判定条件と同様な形で記述される。私はこの判定条件をA∞(X)の特性多項式を求めるものであると考え、Chapter1の議論に沿った形でPX(T)の零点の有理性を仮定しない一般的な判定条件(Chapter2)を完成した。更にこの判定条件を用いて、p=3,k=Q(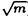 ),1<m<104の範囲で予想の成立を全て確かめた。 ),1<m<104の範囲で予想の成立を全て確かめた。 REFERENCES[B] A.Brumer,On the units of algebraic number fields,Mathematika 14(1967),121-124.[C] A.Candiotti,Computations of Iwasawa invariants and K2,Compositio Math.29(1974),89-111.[FW]B.Ferrero and L.Washington,The Iwasawa invariant 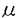 p vanishes for abelian number fields,Ann.of Math.109(1979),377-395.[G] R.Greenberg,On the Iwasawa invariants of totally real number fields,Amer.J.Math.98(1976),263-284.[IS] H.Ichimura and H.Sumida,On the Iwasawa p vanishes for abelian number fields,Ann.of Math.109(1979),377-395.[G] R.Greenberg,On the Iwasawa invariants of totally real number fields,Amer.J.Math.98(1976),263-284.[IS] H.Ichimura and H.Sumida,On the Iwasawa 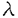 -invariant of the p-cyclotomic field,submitted for publication(1995).[I] K.Iwasawa,On Zl-extensions of algebraic number fields,Ann.of Math.98(1973),246-326.[KS] J.S.Kraft and R.Schoof,Computing Iwasawa modules of real quadratic number fields,Compositio Math.97(1995),135-155.[S] H.Sumida,Greenberg’s conjecture and the Iwasawa polynomial,submitted for publication(1995). -invariant of the p-cyclotomic field,submitted for publication(1995).[I] K.Iwasawa,On Zl-extensions of algebraic number fields,Ann.of Math.98(1973),246-326.[KS] J.S.Kraft and R.Schoof,Computing Iwasawa modules of real quadratic number fields,Compositio Math.97(1995),135-155.[S] H.Sumida,Greenberg’s conjecture and the Iwasawa polynomial,submitted for publication(1995). |