| 内容要旨 | | 標題の論文は次の二部から成る。 [1]:Real Shintani functions on SU(2,1) [2]:An explicite formulae of some type of Shintani functions on SU(3,1) これらの論文で考察する問題及びその背景を説明しよう。 Gを実半単純リー群、KをGの極大コンパクト部分群、gをGのリー環とする。Gの閉部分群Rとそのフレッシェ表現(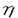 , ,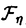 )に対してC∞-誘導表現 )に対してC∞-誘導表現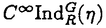 が、G上のC∞-関数F:G→ が、G上のC∞-関数F:G→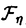 で全てのg∈G及び で全てのg∈G及び ∈RにたいしてF(rg)= ∈RにたいしてF(rg)=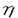 ( ( )F(g)を満たすもの全体に自然な線形位相を与えたフレッシェ空間にGを右移動で作用させることで定義される。この時、次のことを問題にする。 )F(g)を満たすもの全体に自然な線形位相を与えたフレッシェ空間にGを右移動で作用させることで定義される。この時、次のことを問題にする。 (1)与えられた既約(g,K)-加群IIにたいして(g,K)-絡作用素の空間 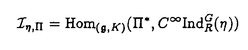 の次元。 (2)Tが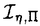 を走る時のImage(T)の合併を を走る時のImage(T)の合併を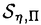 とし、Kの各既約表現( とし、Kの各既約表現( ,W)について ,W)について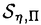 ( ( )=HomK( )=HomK( *, *,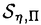 )とおく。 )とおく。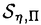 ( ( )に属する関数の明示的公式。 )に属する関数の明示的公式。 PをGの極小放物部分群とする。旗多様体G/PにおいてRが唯一つの開軌道を持つ時RはGのsphericalな部分群と呼ばれる。このようなRにたいしては上で定義した絡作用素の空間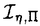 は有限次元になるだろうことが期待される。また、 は有限次元になるだろうことが期待される。また、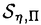 に属する函数は、ある種の一般化された球函数と見なされ保型L-函数の積分表示理論などに姿を表す。例えば、RとしてGの極大べき単部分群を選び に属する函数は、ある種の一般化された球函数と見なされ保型L-函数の積分表示理論などに姿を表す。例えば、RとしてGの極大べき単部分群を選び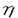 としてRの指標をとった場合、 としてRの指標をとった場合、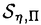 はホイッタカー函数として知られるG上の特殊函数達から成る。ホイッタカー函数はGL(2)の保型表現に付随する標準L-函数のジャッケ-ラングランズ理論を始めとして現在知られている保型L-函数の積分表示理論において主要な道具の一つとして用いられている。(文献[J-L])しかし、ホイッタカー模型を持たない保型表現に対してはこの方法ではL-函数の積分表示は望めない。より多くの保型表現を扱うため種々のRおよび はホイッタカー函数として知られるG上の特殊函数達から成る。ホイッタカー函数はGL(2)の保型表現に付随する標準L-函数のジャッケ-ラングランズ理論を始めとして現在知られている保型L-函数の積分表示理論において主要な道具の一つとして用いられている。(文献[J-L])しかし、ホイッタカー模型を持たない保型表現に対してはこの方法ではL-函数の積分表示は望めない。より多くの保型表現を扱うため種々のRおよび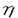 に対する一般化された球関数が研究され、それを用いた積分表示が考案されている。 に対する一般化された球関数が研究され、それを用いた積分表示が考案されている。 さて現在、村瀬篤氏、菅野孝史氏及び加藤信一氏を中心として研究が進められている新谷函数も上で述べたような球函数に他ならない。(文献[M-S])新谷函数を考えるには、RとしてGのある対合の固定点全体として得られるGの簡約可能部分群を取れば良い。この時、半単純対称空間G/Rの構造論の結果からGのベクトル部分群Aが存在して岩澤-カルタン型分解G=RAKが成り立つことが知られている。(文献[R])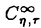 (R\G/K)をC∞-函数F: (R\G/K)をC∞-函数F: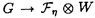 で で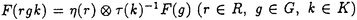 を満たすもの全体の成す空間とし、 を満たすもの全体の成す空間とし、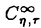 (A)でFが (A)でFが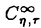 (R\G/K)を走る時そのA-動径成分F|A全体を表すことにすると、分解G=RAKの帰結として同型 (R\G/K)を走る時そのA-動径成分F|A全体を表すことにすると、分解G=RAKの帰結として同型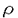 : :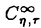 (R\G/K)→ (R\G/K)→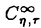 (A)を得る。 (A)を得る。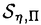 は は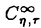 (R\G/K)の部分空間なので本質的に重要なのはその動径成分 (R\G/K)の部分空間なので本質的に重要なのはその動径成分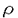 ( (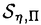 ( ( ))である。 ))である。 論文[1]では, G=SU(2,1), R=S(U(1)×U(1,1)), II:Gの離散系列表現, 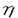 :Rの既約unitary表現, :Rの既約unitary表現, 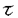 :IIの極小K-タイプ :IIの極小K-タイプ 論文[2]では G=SU(3,1), R=S(U(1)×U(2,1)), II:Gの離散系列表現, 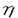 :Rの主系列表現、 :Rの主系列表現、 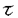 :IIの極小K-タイプ :IIの極小K-タイプ と言う状況のもとで新谷函数の動径成分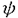 ∈ ∈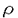 ( (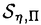 ( ( ))の明示公式を得ると同時に絡作用素の空間 ))の明示公式を得ると同時に絡作用素の空間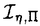 の次元が1以下であることを示した。論文[1]、[2]の内容及び手法を説明しよう。IIをGの離散系列表現、その極小K-タイプを の次元が1以下であることを示した。論文[1]、[2]の内容及び手法を説明しよう。IIをGの離散系列表現、その極小K-タイプを としよう。G/Kの原点における接空間をpとする。K-加群 としよう。G/Kの原点における接空間をpとする。K-加群 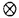 pcの部分K-加群 pcの部分K-加群 ’でHomK( ’でHomK( ’,II|K)={0}を満たすものの中で最大のものを ’,II|K)={0}を満たすものの中で最大のものを -、p -、p -: -: 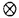 pc→ pc→ -をK-射影子とする。pの正規直交基底{Xi}を一つ選びシュミット作用素と呼ばれる一階微分作用素 -をK-射影子とする。pの正規直交基底{Xi}を一つ選びシュミット作用素と呼ばれる一階微分作用素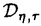 : :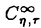 (R\G/K)→ (R\G/K)→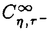 (R\G/K)を (R\G/K)を 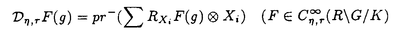 で定義する。山下博氏の一般的な結果によると、 の最高ウエイトが壁から遠いと言う仮定の下で、 の最高ウエイトが壁から遠いと言う仮定の下で、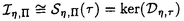 となる。(文献[Y])さて、K となる。(文献[Y])さて、K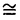 U(n)及びR U(n)及びR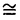 (n-1,1)であることに注意すると、K及びRの与えられた表現 (n-1,1)であることに注意すると、K及びRの与えられた表現 及び 及び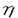 の表現空間の基底としてそれぞれのゲルファント-ゼットリン基底{ の表現空間の基底としてそれぞれのゲルファント-ゼットリン基底{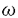 A}及び{ A}及び{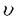 Q}を取ることが出来る。これらの基底にたいしては、K及びRのリー環の作用を具体的に書き表す公式が知られており種々の球函数の計算に利用されている。(文献[G-Z]、[V-K])実際、我々の状況においてもゲルファント-ゼットリン基底は重要な役割を果たす。新谷函数 Q}を取ることが出来る。これらの基底にたいしては、K及びRのリー環の作用を具体的に書き表す公式が知られており種々の球函数の計算に利用されている。(文献[G-Z]、[V-K])実際、我々の状況においてもゲルファント-ゼットリン基底は重要な役割を果たす。新谷函数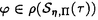 が与えられたとしよう。ゲルファント-ゼットリン基底により が与えられたとしよう。ゲルファント-ゼットリン基底により 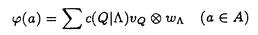 と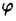 を展開する事が出来る。但し、c(Q|∧)はベクトル群A を展開する事が出来る。但し、c(Q|∧)はベクトル群A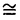 R上のC∞-函数である。論文[1]及び[2]では、まずシュミット作用素の動径成分 R上のC∞-函数である。論文[1]及び[2]では、まずシュミット作用素の動径成分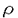 ( (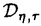 )を )を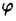 の係数c(Q| の係数c(Q|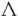 )の言葉で具体的に書き下し、 )の言葉で具体的に書き下し、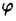 の満たす一階の微分-差分方程式系を導出している。次に、こうして得られた微分-差分方程式系のC∞-解を既知の特殊函数を用いて書き表せば の満たす一階の微分-差分方程式系を導出している。次に、こうして得られた微分-差分方程式系のC∞-解を既知の特殊函数を用いて書き表せば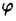 の明示公式が得られることになる。論文[1]及び[2]によれば、上で述べた状況で{c(Q| の明示公式が得られることになる。論文[1]及び[2]によれば、上で述べた状況で{c(Q|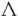 )}は定数倍を除いて一意に決まり各c(Q| )}は定数倍を除いて一意に決まり各c(Q|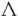 )は )は 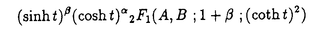 (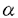 , ,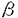 は整数, は整数,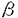 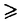 0,A,Bは複素数,2F1(a,b;c;z)はガウスの超幾何級数tはRの標準座標) 0,A,Bは複素数,2F1(a,b;c;z)はガウスの超幾何級数tはRの標準座標) と言う形のA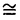 R上の函数(の線形結合)で表示できることが結論される。 R上の函数(の線形結合)で表示できることが結論される。 論文[1]の付録では、IIおよび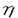 がそれぞれG=SU(2,1)およびR がそれぞれG=SU(2,1)およびR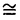 U(1,1)の主系列表現の場合を論じ新谷関数の空間 U(1,1)の主系列表現の場合を論じ新谷関数の空間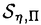 ( ( )が一次元以下であることを示し、その生成元のA動径成分がやはりガウスの超幾何級数で書けることを示した。これは、分解G=RAKに関するカシミール作用素のA-動径成分を計算する事から導かれる。 )が一次元以下であることを示し、その生成元のA動径成分がやはりガウスの超幾何級数で書けることを示した。これは、分解G=RAKに関するカシミール作用素のA-動径成分を計算する事から導かれる。 REFERENCES[G-Z]I.M.Gel’fand-M.L.Zetlin,Finite dimensional representations of the group of unimodular matrices,Dokl.Akad.Nauk.SSSR 71(1950),825-828.[J-L]H.Jaquet-R.Langlands,Automorphic forms on GL(2),Springer Lecture Notes,Vol.114(1970).[M-S]A.Murase-T.Sugano,Shintani function and its application to automorphic L-functions for classical groups I:The case of orthogonal groups,Math.Ann.299(1994),17-56.[R]W.Rossmann,The structure of semisimple symmetric spaces,Can.J.Math.31(1979),157-180.[V-K]N.Ja.Vilenkin-A.U.Klimyk,Representation of Lie Groups and Spherical Functions(vol.3),Mathematics and Its Applications(Soviet Series)Kluwer Academic Publishers(1992).[Y]H.Yamashita,Embedding of discrete series into induced representations of semisimple Lie groups I-General theory and the case of SU(2,2),Japan.J.Math.16(1)(1990),31-95. |
| 審査要旨 | | 提出論文について論ずる前に、少し動機となった背景を述べよう。 保型形式の整数論的研究の柱となる重要な主題の一つに保型的L関数の構成がある。これについては一般線形群上の保型形式についてはJacques-Piateskii-Shapiro-Shalikaの研究があり、Whittaker模型を持つ保型表現について保型的L関数を構成し、Euler積、関数等式、有理型に接続できる、等のことが示されている。 これを他の簡約代数群について考えることは、いろいろな人によって試みられているが、とりわけ菅野孝史-村瀬篤の両氏がA型、BD型の古典群上の正則保型形式に通用する強力な方法を発展させている。また彼らの研究は、完全な関数等式を得ているという意味で、他の類似の研究よりずっと優れたものである。しかしながら、彼らの研究に於いても、いまだ実素点での研究が充分に一般に行われていない。これが本研究の動機の一つである。 もう一つの動機を述べよう。古典的な球関数の種々の公式が、実半単純群の表現論の言葉で意味づけられその後の表現論研究の大きな動機付けになったことは、初期の歴史上よく知られている。その後、高階の群の表現論の研究は著しく代数化された。しかしながら「分類」についての見通しが明らかになるにつれて、少し前より各種の標準的な既約表現の「幾何学的実現あるいは模型」の研究が再び興味をもたれだしている。これは表現論それ自身の興味もさることながら、数理物理との関連に於いて、種々の量子可積分系を得ることも興味あることであるからである。 提出論文は次の二部から成る。 [1]:Real Shintani functions on SU(2,1) [2]:An explicite formulae of some type of Shintani functions on SU(3,1) これらの論文で取り扱う問題を少し一般化して定式化すれば次の様になる。 Gを実半単純Lie群、KをGの極大コンパクト部分群、gをGのLie環とする。Gの閉部分群RとそのFrechet表現(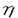 , ,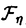 )に対してC∞-誘導表現 )に対してC∞-誘導表現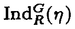 が、G上のC∞-関数F:G→ が、G上のC∞-関数F:G→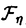 で全てのg∈G及び で全てのg∈G及び ∈RにたいしてF(rg)= ∈RにたいしてF(rg)=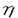 ( ( )F(g)を満たすもの全体に自然な線形位相を与えたFrechet空間にGを右移動で作用させることで定義する。このとき、次の問題を考える。 )F(g)を満たすもの全体に自然な線形位相を与えたFrechet空間にGを右移動で作用させることで定義する。このとき、次の問題を考える。 (1)与えられた既約(g,K)-加群IIにたいして(g,K)-絡作用素の空間 の次元を求める。 (2)Tが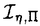 を走る時のImage(T)の合併を を走る時のImage(T)の合併を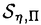 とし、Kの各既約表現( とし、Kの各既約表現( ,W)について ,W)について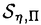 ( ( )=HomK( )=HomK( *, *,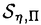 )とおく。 )とおく。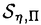 ( ( )に属する関数の明示的公式を得る。 )に属する関数の明示的公式を得る。 PをGの極小放物部分群とする。旗多様体G/PにおいてRが唯一つの開軌道を持つ時RをGの仮にsphericalな部分群と呼ぶ。このようなRにたいしては上で定義した絡作用素の空間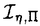 はしばしば有限次元になる。また、 はしばしば有限次元になる。また、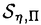 に属する関数は、ある種の一般化された球関数と見なされ保型L関数の積分表示の理論で重要である。例えば、RとしてGの極大unipotent部分群を選び に属する関数は、ある種の一般化された球関数と見なされ保型L関数の積分表示の理論で重要である。例えば、RとしてGの極大unipotent部分群を選び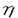 としてRの指標をとった場合、 としてRの指標をとった場合、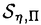 はWhittaker関数として知られるG上の特殊関数から成る。 はWhittaker関数として知られるG上の特殊関数から成る。 さてこの論文の主題の新谷関数を考えるには、RとしてGのある対合の固定点全体として得られるGの簡約可能部分群を取る。するとGのベクトル部分群Aが存在して岩澤-カルタン型分解G=RAKが成り立つ。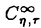 (R\G/K)をC∞-函数F:G→ (R\G/K)をC∞-函数F:G→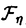 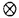 WでF( WでF( g g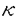 )= )=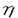 ( ( ) )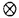  ( (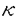 )-1F(g)( )-1F(g)( ∈R,g∈G, ∈R,g∈G,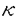 ∈K)を満たすもの全体の成す空間とし、 ∈K)を満たすもの全体の成す空間とし、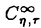 (A)でFが (A)でFが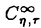 (R\G/K)を走る時そのA-動径成分F|A全体を表すことにすると、分解G=RAKの帰結として同型 (R\G/K)を走る時そのA-動径成分F|A全体を表すことにすると、分解G=RAKの帰結として同型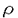 : :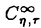 (R\G/K)→ (R\G/K)→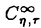 (A)を得る。つまり (A)を得る。つまり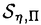 を調べるにはその動径成分 を調べるにはその動径成分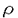 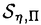 を見ればよい。 を見ればよい。 論文[1]では, II:Gの離散系列表現,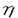 :Rの既約unitary表現, :Rの既約unitary表現, :IIの極小K-タイプ :IIの極小K-タイプ また論文[2]では II:Gの離散系列表現,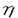 :Rの主系列表現, :Rの主系列表現, :IIの極小K-タイプ :IIの極小K-タイプ と言う状況のもとで新谷関数の動径成分の明示公式を得ると同時に絡作用素の空間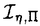 の次元が1以下であることを示した。これが主結果である。 の次元が1以下であることを示した。これが主結果である。 論文の基本的手法を説明しよう。先ず、K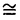 U(n)及びR U(n)及びR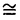 (n-1,1)であることに注意すると、K及びRの与えられた表現 (n-1,1)であることに注意すると、K及びRの与えられた表現 及び 及び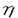 の表現空間の基底としてそれぞれのGelfand-Zetlin基底{ の表現空間の基底としてそれぞれのGelfand-Zetlin基底{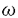 ∧}及び{ ∧}及び{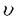 Q}を取ることができる。すると新谷関数は、 Q}を取ることができる。すると新谷関数は、 と展開できる。但し、c(Q|∧)はベクトル群A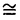 R上のC∞-関数である。これに対して、Schmid作用素の動径成分 R上のC∞-関数である。これに対して、Schmid作用素の動径成分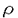 ( (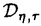 )を )を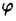 の係数c(Q|∧)の言葉で具体的に書き下し、 の係数c(Q|∧)の言葉で具体的に書き下し、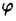 の満たす一階の微分-差分方程式系を導出する。次に、こうして得られた微分-差分方程式系のC∞-解を既知の特殊関数を用いて書き表すことによって、 の満たす一階の微分-差分方程式系を導出する。次に、こうして得られた微分-差分方程式系のC∞-解を既知の特殊関数を用いて書き表すことによって、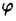 の明示公式が得られることになる。最終的には の明示公式が得られることになる。最終的には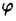 は定数倍を除いて一意に決まり、各c(Q|∧)はガウスの超幾何級数で表示できることが結論される。 は定数倍を除いて一意に決まり、各c(Q|∧)はガウスの超幾何級数で表示できることが結論される。 上記の論文はSU(2,1)については「重複度無し」の新しい証明を、SU(3,1)については「重複度無し」という新しい結果を得ている。また球面部分群の無限次元表現に対する球関数を明示的に調べたという点も、新しい論点である。結果が保型的L関数に応用できるという点でも重要である。 よって、論文提出者都築正男は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |