| 内容要旨 | | 微分方程式や差分方程式などが,その方程式中にいくつかのパラメータを持つ場合,このパラメータが方程式の解空間の変形パラメータとしての役割を持つことがある.例えば,差分方程式における差分間隔や,相互作用の強度,流体における粘性といったものがこのパラメータとして考えられる.特に,このパラメータが解空間の持つ性質を保存する良いパラメータである場合,このパラメータについての極限によって得られる解空間を調べることにより,パラメータの値が一般の場合の解空間についての情報が引き出せることがある.可積分系については,差分化や剛体化のパラメータなどがこのような良いパラメータとして知られている.可積分系ではこの極限の結果得られる解空間がが単純なものであることが期待され,ある極限では系がmax等の組合せ論的な関数で記述できる.これは,系の状態の変化がある種の組合せ論的アルゴリズムとして記述できることを意味している.本論文では,有限質点の可積分系である戸田分子方程式の固有値パラメータによる変形,無限質点の可積分系である戸田格子方程式の基礎体の変形による極限,およびその保存量の場合について,系の組合せ論的特徴,時間発展と線形計画法との関係等について述べる. 1 戸田分子方程式の場合 戸田分子方程式[1] 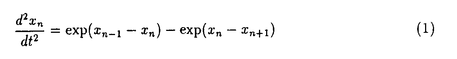 は,境界条件  によって有限質点の方程式となり,変数 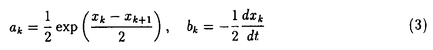 の導入により,行列形式  に書くことが出来る.ここで,  である.さらに, eを(0,0,...,1)Tとして,関数 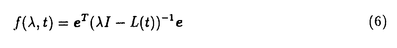 を導入すると,系の時間発展は,この関数の留数の時間発展 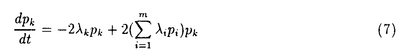 と等価である.[2]この方程式は厳密に解くことが出来て,その解は 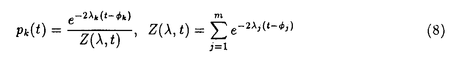 となる.f(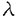 ,t)の極は行列Lの固有値としての意味を持っており,系の時間発展に対して変化しない.この固有値 ,t)の極は行列Lの固有値としての意味を持っており,系の時間発展に対して変化しない.この固有値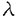 1< 1<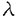 2…をパラメータと考えて,1/ 2…をパラメータと考えて,1/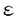 倍する変形を考える,特に 倍する変形を考える,特に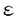 →0という極限では,留数ベクトルの時間発展は, →0という極限では,留数ベクトルの時間発展は,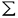 p(k)=1,p(1)>0,p(2)>0,…,p(m)>0という単体の上の頂点の移動としてとらえられる.この単体は一種の確率測度の空間を表しており,この頂点の運動は線形計画問題の解法の一種である単体法としてとらえることができる.実際に,線形計画問題の最大化関数としてはモーメント関数 p(k)=1,p(1)>0,p(2)>0,…,p(m)>0という単体の上の頂点の移動としてとらえられる.この単体は一種の確率測度の空間を表しており,この頂点の運動は線形計画問題の解法の一種である単体法としてとらえることができる.実際に,線形計画問題の最大化関数としてはモーメント関数 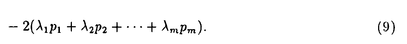 を取ればよい.このモーメント関数の最大化を単体法で行なった場合の軌道と,戸田分子方程式の解の極限で得られる軌道とは1対1に対応していることが示せる.またその頂点の時間発展の跳躍時刻等の細部の情報は,pの双対に相当するl=(l1,l2,…,lm),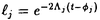 によって決められており,系の時間変化は最大化問題 によって決められており,系の時間変化は最大化問題  と同等である. 2 半体戸田格子の場合 半体とは,以下のような公理を満たす二項演算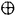 , ,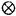 の上の代数系であり,体ではないが列車の発着や窓口サービスの問題など様々な応用を持っている.[3] の上の代数系であり,体ではないが列車の発着や窓口サービスの問題など様々な応用を持っている.[3] 1)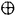 は可換で結合的 は可換で結合的 2)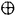 は冪等,つまりa は冪等,つまりa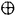 a=aが成り立つ. a=aが成り立つ. 3)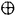 について零元 について零元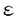 ∈Kを持つ. ∈Kを持つ. 4)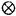 は可換で,非零元上に群を作る. は可換で,非零元上に群を作る. 5)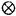 は単位元e∈Kを持つ. は単位元e∈Kを持つ. 6)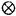 と と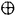 は分配則を満たす. は分配則を満たす. このうち,公理2)については,計算上の制限が必要な場合がある.演算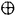 はこのままでは可逆ではないので,可逆となるように代数系を拡張し, はこのままでは可逆ではないので,可逆となるように代数系を拡張し,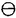 aという要素を付け加える.通常の代数系と異なり,半体の上での方程式には注意を要するが,バランスと方程式という概念を両方導入することによって,線形システムやその上の行列式といった概念を考えることが出来る.特によく用いられる半体としてa aという要素を付け加える.通常の代数系と異なり,半体の上での方程式には注意を要するが,バランスと方程式という概念を両方導入することによって,線形システムやその上の行列式といった概念を考えることが出来る.特によく用いられる半体としてa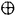 bをmax(a,b),a bをmax(a,b),a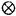 bをa+bとしてもつ実数半体R=RU-∞があり,この上の行列式 bをa+bとしてもつ実数半体R=RU-∞があり,この上の行列式 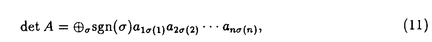 は,最大化問題としてとらえることができると考えられる.実際にそれは最適割り当て問題という線形計画問題に等しく,最適割り当て問題における多面体は,戸田分子の場合に比べると若干複雑な複確率行列 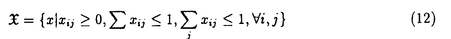 という集合である. 半体戸田格子方程式は,tを時間変数,nを空間変数と考えて 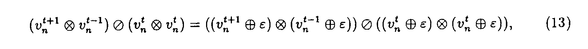 という実数半体上の偏差分方程式であり,[4],[5]このソリトン解は 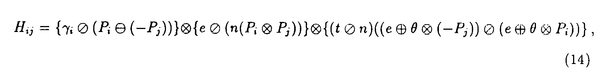 という行列を用いて,det(I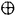 H)と表すことが出来る.ここで,Pi, H)と表すことが出来る.ここで,Pi,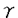 i等は任意パラメータ,Iは単位行列, i等は任意パラメータ,Iは単位行列,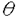 は定数である.半体戸田格子ソリトンもまた多面体の上の頂点の移動と考えることができ,それは最大化問題 は定数である.半体戸田格子ソリトンもまた多面体の上の頂点の移動と考えることができ,それは最大化問題  と同等である.[4] 3 オートマトン系の場合 半体戸田格子の系の一つとして,半体Volterra方程式があるが,これはオートマトン系として組合せ論的な時間発展を持つことが知られている.[6]その保存量はDyck言語やYoung図形といった組合せ論的な方法を用いて構成することができその方法はRobinson-Schensted対応になっている.その結果得られる保存量はYoung図形の形となって現れる.[7]Dyck言語とは正しく対応づけられる(と)の列で,系の時間発展は対応するDyck言語の上の時間発展を促すが,その時間発展は次のようなDyck言語に対する関数の最大化過程としてとらえられる.ひとつのDyck言語をD=D1,D2,…と書き,次のように各文字に数を対応づける. 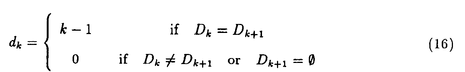 この数に対して,f(D)=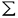 dkとする.この値はDyck言語D(t)が時間発展するとともに増大する.この過程はある形を定めたときのYoung図形上の盤のなす格子の頂点の運動と考えることができる. dkとする.この値はDyck言語D(t)が時間発展するとともに増大する.この過程はある形を定めたときのYoung図形上の盤のなす格子の頂点の運動と考えることができる. 参考文献[1]Morikazu Toda,Nonlinear waves and solitons,KTK Scientific publishers,1989[2]Jurgen Moser,Finitely Many Mass Points on the Line under the Influence of Exponential Potential-an Integrable System,Lecture Notes in Physics,38(1975),467-497.[3]Francois Louis Baccelli,Guy Cohen,Geert Jan Olsder,Jean-Pierre Quadrat.Syncronization and Linearity.(John Wiley & Sons,1992).[4]Tetsuji Tokihiro,to appear.[5]Junta Matsukidaira,Daisuke Takahashi,to appear.[6]D.Takahashi and J.Satsuma,J.Phys.Soc.Jpn.59(1990)3514.[7]Makoto Torii,Daisuke Takahashi and Junkichi Satsuma,Physica D.to appear. |
| 審査要旨 | | 微分方程式や差分方程式などが方程式中にいくつかのパラメータをもつ場合,それらが解空間の変形パラメータとしての役割を果たすことがある.とくに,このパラメータを変化させても解空間の基本的な性質が保存する場合には,パラメータについて極限をとったときの解空間を調べることにより,パラメータの値が一般のときの解空間に関する情報が引き出せることがある.可積分系については,差分化や剛体化に関連したパラメータなどがこのような性質をもっている.可積分系では極限の結果得られる解空間は構造が単純であり、ある場合にはmax等の組合せ論的な関数で解が表わされる.このことは同時に、系の状態の変化がある種の組合せ論的アルゴリズムとして記述できることを意味している. 本論文では,第1章で変形パラメータに関する以上の見解を述べたのち,いくつかの可積分方程式について,それらの組み合わせ論的構造を考察している.第2章では、戸田分子方程式の固有値パラメータによる変形を取り扱い、第3章では戸田分子方程式の解とフラクタル次元との関係について議論を行っている.また,第4章では戸田格子方程式の基礎体の変形による極限を取り扱い,第5章ではある種のボルテラ系と関連したセルオートマトンについて,保存量の組合せ論的特徴,時間発展と線形計画法との関係等について述べている.最後に,第5章で結語を与えている.第2章から第5章で得られた結果はそれぞれ以下のようにまとめることができる. 第2章で対象としている方程式は,質点の数が有限個の非線形格子を記述する戸田分子方程式,d2xn/dt2=exp(xn-1-xn)-exp(xn-xn+1),である.この式は,適当な変数を導入することにより,行列形式,dL/dt=[M,L],に書くことが出来る.さらに,eを(0,0,...,1)Tとして,関数f(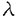 ,t)=eT( ,t)=eT(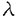 I-L(t))-1eを導入すると,戸田分子方程式は,この関数の留数の時間発展を支配する式 I-L(t))-1eを導入すると,戸田分子方程式は,この関数の留数の時間発展を支配する式 と等価になる.また,関数f(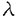 ,t)の極は行列Lの固有値としての意味を持っており,系の時間発展に対して変化しない.本論文ではこれらの事実に基づき,固有値 ,t)の極は行列Lの固有値としての意味を持っており,系の時間発展に対して変化しない.本論文ではこれらの事実に基づき,固有値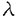 1< 1<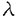 2<…をパラメータとして,それらを1/ 2<…をパラメータとして,それらを1/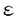 倍する変形を考えている.その結果,とくに 倍する変形を考えている.その結果,とくに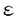 →0という極限において.留数ベクトルの時間発展がある単体上の頂点の移動としてとらえられること,および,この単体が一種の確率空間を表しており,この頂点の運動は線形計画問題の解法の一種である単体法とみなせることを指摘している. →0という極限において.留数ベクトルの時間発展がある単体上の頂点の移動としてとらえられること,および,この単体が一種の確率空間を表しており,この頂点の運動は線形計画問題の解法の一種である単体法とみなせることを指摘している. 第3章では,戸田分子方程式の解空間が確率空間と見なせること,確率空間上ではエントロピー関数が解の構成に重要な役割を果たすこと,および,確率的な構造を有する集合においてはフラクタル次元がエントロピー関数として定義できることを用いて,戸田分子の時間発展がフラクタル次元の時間発展と等価になるという解釈を与えている. 次に第4章では,2章で用いたのと同様の極限操作を戸田格子方程式に対して行うことにより得られるセルオートマトン系を議論している.まず,この系が半体と呼ばれる代数でよく記述されることを指摘したのち,戸田格子の時間発展は最大化問題と等価であると述べている.また,その問題は最適割り当てとよばれる線形計画問題に等しく,解に現れる多面体が複確率行列になることを示している. 最後に第5章ではボルテラ方程式から得られるセルオートマトン系を取り扱っている.まず,その保存量がDyck言語やYoung図形といった組合せ論で用いられるものにより構成できることを述べたのち,それらの方法がRobinson-Schensted対応になっていること,および,得られる保存量がYoung図形上の盤の形となって表わされることを示している.さらに,オートマトン系の時間発展は,対応するDyck言語で書かれる関数の最大化過程と解釈できること,および,その過程がある形を定めたときのYoung図形上の盤のなす格子の頂点の運動と考えられることを明らかにしている. 以上,本論文で取り扱われている内容は具体的であり,可積分系についての新しい問題提起を行なっている.また,得られた結果も数理科学における応用と一般化が期待され,興味深いものである.よって,論文提出者 鳥居 真 は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. |