学位論文要旨
| No | 112115 | |
| 著者(漢字) | 永井,敦 | |
| 著者(英字) | NAGAI,Atsushi | |
| 著者(カナ) | ナガイ,アツシ | |
| 標題(和) | 離散可積分系と加速法 | |
| 標題(洋) | Discrete Integrable Systems and Convergence Acceleration Methods | |
| 報告番号 | 112115 | |
| 報告番号 | 甲12115 | |
| 学位授与日 | 1996.03.29 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第50号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | ||
| 論文審査委員 | ||
| 内容要旨 | 最近,「数値計算の優れたアルゴリズムの背後には可積分系の構造がある」と言われている.本論文では数列の加速法とソリトン方程式との関連および可積分系の概念に基づく加速法の拡張について報告する. 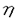 アルゴリズムと アルゴリズムと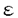 アルゴリズム アルゴリズム数列1 1実際は, のm→∞での極限S∞の近似値を求める際,直接計算すると大量のデータが必要になることがある. 以上の変換を施した後, 式(3)は従属変数変換 によって次の離散型KdV方程式と等価になる. このことから ここで, の形に書ける.nが大きくなると,奇数項 さらに無限級数に対する 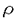 アルゴリズム アルゴリズム 加速法の1つ, 第1に加速法としての性能の違いである. 第3に の1つの可積分な離散化と考えられる. 前述の通り, 式(17)で与えられるアルゴリズム(Thieleの Papageorgiouらは式(18)について非線形差分方程式の可積分系のチェックに用いられる特異点閉じ込め法(singularity confinement test)を適用した.その結果, を満たすとき,このテストをパスすることが示された. この"可積分な"アルゴリズム(PGRアルゴリズム)について, のとき,1変数を消去することによって,離散型パンルベ方程式のI型, が得られることがわかった. またPGRアルゴリズムの加速法としての性能はどうなるか?これまでに数値実験をいろいろなケースで行なってきたが,直観的にいうと加速はよくない.しかし,特殊な場合として, のとき,かなり広いクラスの数列を加速する. 数列の加速法の1つである では他のアルゴリズムは何らかの可積分なソリトン方程式になっているのか?他の離散型ソリトン方程式を考えたり,または行列式の構造を変形したりすることによって,新しい加速法を作れるのか? 言い替えれば数列を加速するということと離散方程式が可積分であるということはどのように関連するのか?その他にも固有値計算や線形計画問題において非線形可積分系の構造があることが報告されているが,どうして数値計算のアルゴリズムとソリトン方程式が一致するのか?この問題の解明によるソリトン理論の数理工学への応用,これを今後の課題としたい. | |
| 審査要旨 | 近年,数値計算の優れたアルゴリズムの背後には可積分系の構造があることが指摘されはじめている.本論文ではアルゴリズムのうちとくに数列の加速法に着目し,それと可積分系の代表例であるソリトン方程式との関連について考察を加えている.また,その結果に基づいて新しい加速法を提案している. 数列の加速法とは次のような方法をいう.数列,S0,S1,S2,…,Sm,…のm→∞での極限S∞の近似値を求める際,直接計算すると大量のデータが必要になることがある.そこで適当な変換をほどこした数列に対して計算を行ない,より速く極限S∞に収束させる.問題は変換のアルゴリズムと収束の程度である.加速法にはさまざまなものがあるが,本論文で対象としたのは, 論文ではまず漸化式
で与えられる 次に論文で取り扱ったのは漸化式
で与えられる
の形に自然に拡張されることを示したのち,このアルゴリズムは従来の 論文では最後に
を考察している.このアルゴリズムは最近Papageorgiouらが特異点閉じ込め法を利用して,
を満たすとき可積分となることを示したものである.論文提出者は,まずこの可積分なアルゴリズム(PGRアルゴリズム)について,
のとき,1変数を消去することにより,離散型パンルベ方程式のI型の特別な場合になることを見いだしている.また,の場合に広いクラスの数列を加速することを数値実験により示している. 以上,本論文ではさまざまな数列の加速法と可積分系との関連を考察し,それら両者に対して新しい知見を加えている.また,得られた結果は数理工学を含む数理科学における応用と一般化が期待されるものである.よって,論文提出者 永井 敦 は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/53915 |
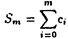 のように無限級数の形の問題が多い.
のように無限級数の形の問題が多い.
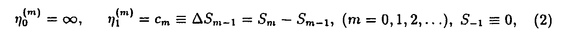
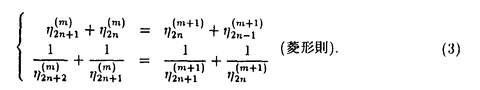
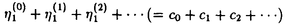 を直接計算するよりも
を直接計算するよりも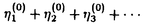 を計算するほうがより速く極限S∞に収束することが知られている.
を計算するほうがより速く極限S∞に収束することが知られている.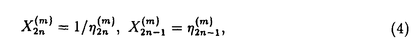
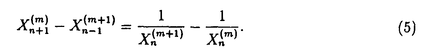
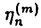 はHankel行列式の比で表されることがわかる.
はHankel行列式の比で表されることがわかる.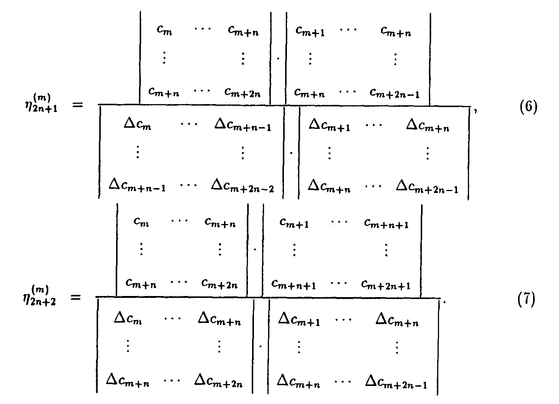
 はmに関する前進差分である.
はmに関する前進差分である.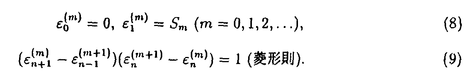
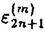 はより速く
はより速く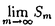 に収束し,他方偶数項
に収束し,他方偶数項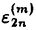 は発散する.Papageorgiou,Grammaticos,及びRamaniは
は発散する.Papageorgiou,Grammaticos,及びRamaniは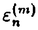 もHankel行列式の比の形になることがわかる.
もHankel行列式の比の形になることがわかる.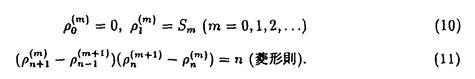
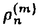 は2重Casorati行列式を用いて表される.
は2重Casorati行列式を用いて表される.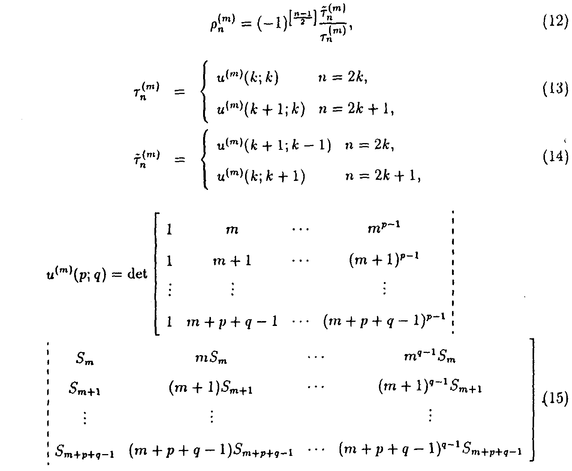
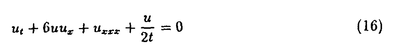
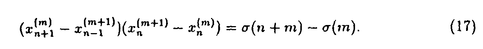
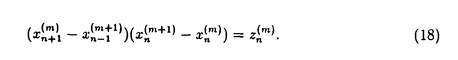
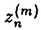 が
が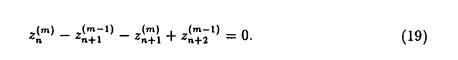
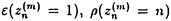 ,及びThieleの
,及びThieleの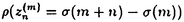 アルゴリズムは条件(19)を満たしている.
アルゴリズムは条件(19)を満たしている.