| 内容要旨 | | この論文は2部から成り、それぞれ独立した内容を持つ。以下、順番にその要旨を述べる。 第1部 磁場中の2次元電子系におけるホール伝導度の導出 磁場中の2次元電子系において、電気伝導度の非対角成分(ホール伝導度と呼ばれる)が量子化されるという現象が1980年に発見され(「量子ホール効果」)、以来理論、実験両側面からの研究が盛んに行われている。理論的研究でよくとられるアプローチは(バルク状態のモデルでは)、電気伝導度を計算しそれを式変形してある種の位相不変量を導くというものである。この電気伝導度を求めるのに理論物理学でよく使われるのは久保公式で、これは線形応答理論を用いるものであるが、その数学的厳密性は今だ確立されているとはいえない。 一方、数学的な研究としてはAvron,Seiler,Yaffeらの仕事がある。ここでは、有界領域における多体シュレーデインガー方程式がモデルとなり、断熱近似を用いた計算により、ホール伝導度を波動関数の値をとる空間でのチャーンクラスとみなすことによってホール伝導度の量子化が証明されている。またBellissardは2次元ユークリッド空間上の1体シュレーディンガー方程式をモデルとし、緩和時間近似を用いた計算で、ホール伝導度をConnesの非可換微分幾何に現れるチャーンクラスとみなすことにより量子化を証明している。 そこで、第1章では新しくより簡明なホール伝導度の定義を考え、その量子化を導いた。これはBellissardのセッティングを使用し、Avronらのアイデアを取り入れたものになっている。第2章ではBellissardのホール伝導度の導出を数学的に厳密化して証明した。 第1章断熱近似による方法 出発点となるハミルトニアンは、 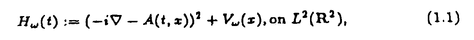 である。ここで、A(t,x)=(A1(x)+f(t),A2(x))でA0=(A1(x),A2(x))はx3方向の定磁場Bに対応するベクトルポテンシャル、f(t)(これはx1方向の電場に相当している)はf(0)=0,f(1)=1,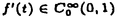 を満たす実数値関数である。 を満たす実数値関数である。 (x)∈L∞(R2)は殆ど至る所有界な関数であり、 (x)∈L∞(R2)は殆ど至る所有界な関数であり、 は確率空間 は確率空間 の元で、かつ任意の の元で、かつ任意の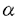 ∈R2に対して ∈R2に対して 上の平行移動Taが存在し、 上の平行移動Taが存在し、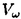 (x+a)= (x+a)=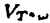 (x)を満たすものとする。 (x)を満たすものとする。 電場を小さくしたときの極限を考えるために、s=t/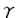 とおいて、時間に関するスケール変換を行う。対応する とおいて、時間に関するスケール変換を行う。対応する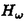 (t)の発展作用素 (t)の発展作用素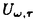 (t)を用い、ホール伝導度を絶対温度零での熱力学的極限として以下のように定義する。 (t)を用い、ホール伝導度を絶対温度零での熱力学的極限として以下のように定義する。 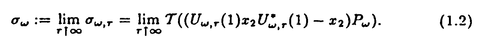 ここで、Tは単位面積当たりのトレース、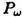 は は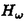 (0)の最低固有状態からあるエネルギー (0)の最低固有状態からあるエネルギー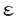 Fまでに対応するスペクトル射影作用素である。 Fまでに対応するスペクトル射影作用素である。 これを近似して調べるために、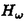 (t)の断熱発展作用素 (t)の断熱発展作用素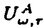 (t)を用いて、以下のものを考える。 (t)を用いて、以下のものを考える。 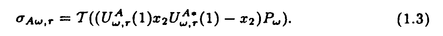 (1.2)、(1.3)の存在と性質を調べることが第1章の目的である。 ここで、 Fは Fは (0)のスペクトルのギャップにあると仮定する(Bを十分に大きくとれば、 (0)のスペクトルのギャップにあると仮定する(Bを十分に大きくとれば、 (0)のスペクトルはギャップを持つ)。 (0)のスペクトルはギャップを持つ)。 上のTa(a∈R2)に関するエルゴード確率測度をPとするとPに関して殆ど至る所の 上のTa(a∈R2)に関するエルゴード確率測度をPとするとPに関して殆ど至る所の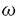 ∈ ∈ について、以下の結果を得る。 について、以下の結果を得る。 定理1.1 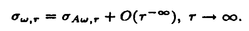 この定理は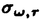 の代わりに の代わりに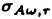 を考えれば十分であることを示す。 を考えれば十分であることを示す。 定理1.2 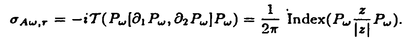 ここで、z=x1+ix2、OjA:=i[A,xj],j=1,2である。第1の等式は(1.2)の存在を、第2の等式はその量子化を示している(これは整数量子ホール効果に対応する)。更に第1章では、有限温度でのホール伝導度の温度零極限における指数型挙動を調べ、更に、時間に依存する周期型ポテンシャル下での電気伝導度の非対角成分が以上の方法で求められることを述べる。 第2章アーベル極限による方法 ここで用いるハミルトニアンは 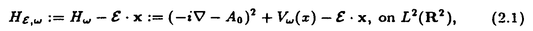 である。ここで、A0と (x)は第1章と同じ仮定を満たし、 (x)は第1章と同じ仮定を満たし、 ∈R2は定常な電場を現している。アーベル極限を用いて、電場により引き起こされる電流を以下のように定義する。 ∈R2は定常な電場を現している。アーベル極限を用いて、電場により引き起こされる電流を以下のように定義する。 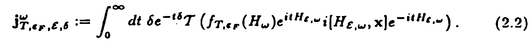  ( (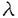 )はフェルミーディラック分布関数で、Tの定義は第1章と同じである。 )はフェルミーディラック分布関数で、Tの定義は第1章と同じである。 (2.2)をj= 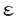 という形にかくと、 という形にかくと、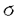 (伝導度テンソル)の非対角成分がホール伝導度に対応するが、それを (伝導度テンソル)の非対角成分がホール伝導度に対応するが、それを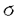 H(T, H(T,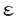 F, F,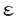 , ,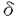 )とする。第1章と同様、 )とする。第1章と同様、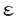 Fは Fは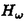 のスペクトルのギャップにあるとすると、Pに関して殆ど至る所の のスペクトルのギャップにあるとすると、Pに関して殆ど至る所の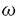 ∈ ∈ について、以下の結果を得る。 について、以下の結果を得る。 定理2. 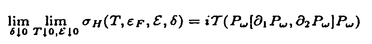 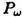 、 、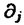 の定義は第1章と同様である。上の定理は第1章と同様の結果が異なるハミルトニアン の定義は第1章と同様である。上の定理は第1章と同様の結果が異なるハミルトニアン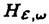 から得られることを示す。 から得られることを示す。 第2部強磁場下での分子の振る舞いについて 中性子星の理論は観測されているパルサーの性質をよく説明するが、この中性子星の表面は主に鉄原子で占められており、重力崩壊の為1012〜1013Gまたはそれ以上のオーダーの強い磁場が存在するといわれている。表面の状態については物理学者により長い間研究されてきたが、数学的な研究としては、Lieb,Solovej,Yngvasonらの仕事を主に挙げることができる。彼らは、この問題をクーロンカで相互作用する多体電子系の最低固有エネルギーの強磁場及び多体極限での漸近挙動として定式化した。この結果によると、磁場の強さBと核の電荷Zとの相互関係によって以下の5通りに場合分けできる(B≪ZaとはZ→∞のとき、B/Za→0となることとする):(1)B≪Z4/3(2)B〜Z4/3(3)Z4/3≪B≪Z3(4)B〜Z3(5)Z3≪B。それぞれの領域で妥当な近似理論が展開され、最低固有エネルギーの漸近挙動が調べられている。 第2部の第1章は、上の(3)〜(5)の領域で成り立つDensity matrix theoryを分子モデルに拡張した場合について調べる。分子モデルへと拡張する理由は、強磁場下で起こる原子同士の束縛の様子を調べることと、第2章でHartree-Fock近似を使うときにこの理論を応用するためである。第2章では、Hartree-Fock近似を用いて同じ問題を調べる。Hartree-Fock近似についてはB=0のときに、Lieb,Simon,Lions,Bach,Graf,Solovejによってよく研究されているが、ここでは(1)〜(5)のどの場合にもHartree-Fock近似が適用できること、上で使われた近似理論よりもHartree-Fock近似の方が誤差が小さいことなどを示す。第3章では、(1)〜(3)で登場するMagnetic Thomas-Fermi theoryで求められたエネルギーの(絶対温度零での)熱力学的極限について調べる。 第1章Density matrix theoryの拡張について ここで考えるのは、∧NL2(R3;C2)上のハミルトニアンとして 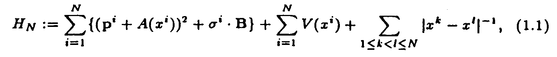 である。ここで、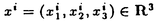 はi番目の粒子の座標、pi=-iO/Oxiは対応する運動量演算子、A(x)=Bxxはx3方向の定磁場B>0に対応するベクトルポテンシャル、 はi番目の粒子の座標、pi=-iO/Oxiは対応する運動量演算子、A(x)=Bxxはx3方向の定磁場B>0に対応するベクトルポテンシャル、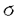 はパウリのスピン行列、 はパウリのスピン行列、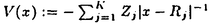 はK個の核(電荷をZj>0)によるクーロンポテンシャルである。 はK個の核(電荷をZj>0)によるクーロンポテンシャルである。 (1.1)の最低固有エネルギーを次のように定義する。 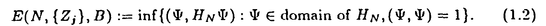 我々の目標は、Zj=kjZとおきN/Z>0を固定してB=O(Za)という関係を保ちなからZ→∞としたときの、E(N,{Zj},B)の挙動を求めることである(普通の分子を考えているのでN/Z>0を固定することは自然である。Z→∞は分子量の大きな分子を考えていることを意味する)。我々はまず、Z4/3≪Bのとき、全ての電子は漸近的に最低ランダウバンドにあるとしてよいことを示す。そのために、最低ランダウバンドへの射影作用素を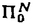 とし、 とし、 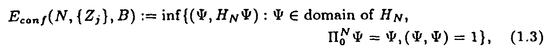 とおくと、次の結果を得る(以降、N/Z>0は固定されているものとする)。 定理1.1 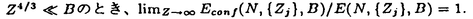 最低ランダウバンドでは電子のスピンは皆下向きであり、運動量はx3方向のみが残る。そこでエネルギーをDensity matrixの汎関数で近似することを考える。その為に、x=(x1,x2,x3)=(x⊥,x3)とかき、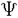 に対応するDensity matrix に対応するDensity matrix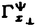 (x,y)を次のように定義する。 (x,y)を次のように定義する。 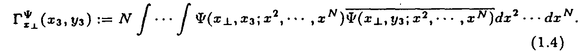 これはx⊥∈R2上のL2(R)-有界作用素値関数として意味を持つ。これを用いて、(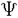 ,HN ,HN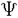 )を次のように近似する。 )を次のように近似する。 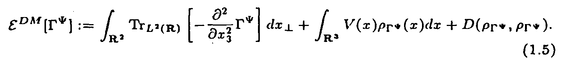 但し、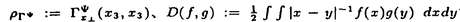 であり、 であり、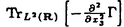 は は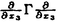 のL2(R)上の作用素としてのトレースである。この(1.5)では第3項において相関エネルギーを無視するという近似がなされている。 のL2(R)上の作用素としてのトレースである。この(1.5)では第3項において相関エネルギーを無視するという近似がなされている。 DMを使った最小化問題を考える。 DMを使った最小化問題を考える。 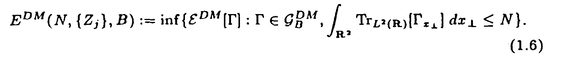 但し、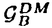 は本文中で定義される は本文中で定義される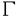 の定義域である。次の定理はEDM(N,{Zj},B)がE(N,{Zj},B)に漸近的に等しくなることを示す。 の定義域である。次の定理はEDM(N,{Zj},B)がE(N,{Zj},B)に漸近的に等しくなることを示す。 定理1.2 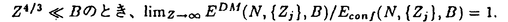 その他に第1章では、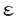 DM[ DM[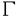 ]を最小にする ]を最小にする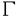 の存在と一意性、エネルギーの各項の収束などを論じる。 の存在と一意性、エネルギーの各項の収束などを論じる。 第2章強磁場下でのHartree-Fock近似 第1章と同じ問題をHartree-Fock近似を用いて調べることを考える。Hartree-Fockエネルギーは、Slater行列式で表された波動関数の中での最低固有エネルギーとして定義される。 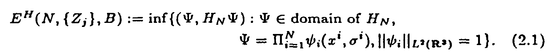 但し、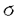 iはi番目粒子のスピン変数である。Hartree-Fock方程式は(2.1)のEuler-Lagrange方程式として得られ、その解の存在と一意性、指数型減衰などが示される。E(N,{Zj},B)との関係は、 iはi番目粒子のスピン変数である。Hartree-Fock方程式は(2.1)のEuler-Lagrange方程式として得られ、その解の存在と一意性、指数型減衰などが示される。E(N,{Zj},B)との関係は、 定理2. 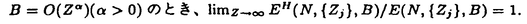 第3章Magnetic Thomas-Fermi theoryの熱力学的極限 中性子星の表面の状態が固体かどうかについて、多くの議論がなされてきている。Hartree-Fock theoryを用いた数値計算で原子同士の束縛は起こらないという結果があるが、一方、Lieb,Solovej,YngvasonらはZ3≪Bの領域で束縛が起こりうることを示した。ここではそれに関連して、(1)〜(3)で適用されるMagnetic Thomas-Fermi theoryの多体極限における単位体積あたりのエネルギーの存在と性質を調べた。 Magnetic Thomas-Fermi theoryは次のように定式化される。 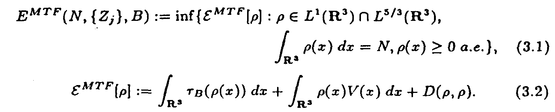 ここで、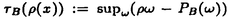 、 、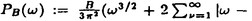 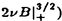 である。 である。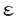 MTF[ MTF[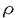 ]を最小化する ]を最小化する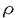 の存在と一意性及びEMTF(N,{Zj},B)との関係についてはLieb,Solovej,Yngvasonが明らかにしている。 の存在と一意性及びEMTF(N,{Zj},B)との関係についてはLieb,Solovej,Yngvasonが明らかにしている。 熱力学的極限を考える為にAをZ3の有限集合とし、VA(x):=-Z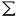 y∈A|x-y|-1とする。(3.1)(3.2)においてN=Z|A|、V=VAとし、 y∈A|x-y|-1とする。(3.1)(3.2)においてN=Z|A|、V=VAとし、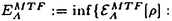 : :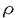 ∈L1(R3)∩L5/3(R3), ∈L1(R3)∩L5/3(R3),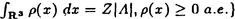 、 、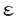 MTFA:= MTFA:=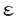 MTF+Z2/2 MTF+Z2/2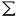 y,x∈A,y≠x|y-z|-1とおく(第2項は核同士のクーロン反発を表わしている)。 y,x∈A,y≠x|y-z|-1とおく(第2項は核同士のクーロン反発を表わしている)。 定理3. 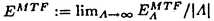 が存在する。 が存在する。 A→∞の定義やEMTFのより具体的な形については本文中で述べる。(以上) |
| 審査要旨 | | 本論文は,磁場中のシュレーディンガー方程式の解の挙動について,物理で知られているいくつかの現象に対し,数学的な証明を与えたものである. 論文は二部からなっている.第一部に於いては,量子ホール効果に関する久保の公式をある現実的な設定の下で断熱近似により厳密に導いている.考察されるシュレーディンガー方程式は という時間依存のハミルトニアンに対応するものであり,ここにベクトルポテンシャルA(t)=A0+(f(t),0)は一様磁場Bをx1軸方向のパルスにより摂動したものであり,fはf(0)=0,f(1)=1,を満たす実数値函数である.また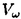 (x)∈L∞(R2)はある確率空間 (x)∈L∞(R2)はある確率空間 上のランダムポテンシャルで, 上のランダムポテンシャルで, 上の平行移動Taに対して 上の平行移動Taに対して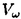 (x+a)= (x+a)=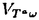 (x)という周期性を持っているとする.従って実際には (x)という周期性を持っているとする.従って実際には はV(x)∈L∞(R2)の平行移動全体の汎弱閉包と考えて良い. はV(x)∈L∞(R2)の平行移動全体の汎弱閉包と考えて良い. 量子ホール効果とはfが作る電場がホール効果により引き起こすx2軸方向の起電力に対する伝導度が,微弱な電場のときにとびとびの値に量子化される現象を云う.物理現象としては1980年頃発見され,von Klitzingらは,これによってノーベル物理学賞を受けた.その理論的説明は,Thoulessらによってなされ,これに対する厳密化の試みはAvron-Seiler-Yaffe1987等により断熱近似を用いた理論が提出されたが,彼らの考察は有界領域の場合だけで,物理的には満足できるものではなかった.これに対しBellissard 1994は,全空間の場合にスペクトル射影作用素とその交換子のトレースという形でホール伝導度を表す公式を与えた.その物理的説明は,統計力学的な「久保の公式」を証明無しに適用した物であった. 本論文の第一部第一章では,上記モデルに対しAvron-Seiler-Yaffeの断熱近似の方法を拡張して,Bellissardの公式を厳密に導き,これを用いて久保の公式を数学的に正当化している.すなわち,まず時間に関するスケール変換s=t/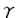 により,電場を小さくした極限を により,電場を小さくした極限を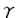 →∞の極限と解釈し,これに対応するハミルトニアンの発展作用素 →∞の極限と解釈し,これに対応するハミルトニアンの発展作用素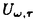 を導入して,ホール伝導度を絶対温度0での熱力学的極限として を導入して,ホール伝導度を絶対温度0での熱力学的極限として により定義する.ここに,Tは単位面積当たりの局所トレースを表し,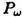 は は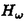 (0)の最低固有状態からフェルミエネルギー (0)の最低固有状態からフェルミエネルギー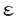 Fまでのスペクトル部分空間への射影作用素である.また, Fまでのスペクトル部分空間への射影作用素である.また,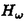 (t)の断熱近似に対して同様の構成によりホール伝導度の断熱近似 (t)の断熱近似に対して同様の構成によりホール伝導度の断熱近似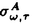 を定義する. を定義する.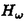 にスペクトルギャップが存在するという,物理的に自然な仮定の下で. にスペクトルギャップが存在するという,物理的に自然な仮定の下で.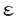 Fがそこから取られている限り,これらの諸量の存在が厳密に確かめられ,断熱近似が元のものに指数的漸近すること Fがそこから取られている限り,これらの諸量の存在が厳密に確かめられ,断熱近似が元のものに指数的漸近すること が示され,次いで断熱近似が という式を満たすことが示される. 続いて第二章では,定常電場のハミルトニアン から により電流を定義し,j=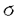 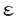 と書いたときの係数行列の非対角成分としてホール伝導度 と書いたときの係数行列の非対角成分としてホール伝導度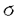 H(T, H(T,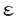 F, F,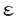 , ,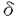 )を解釈するとき,これからa.e. )を解釈するとき,これからa.e.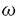 についてT→0, についてT→0,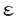 →0, →0,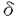 →0というアーペル式極限でも同じ値が得られることを示している. →0というアーペル式極限でも同じ値が得られることを示している. 第三章では,以上の議論をN体ハミルトニアンの場合に一般化し,分数量子ホール効果の正当化を試みている. 第二部は,原子の質量が非常に大きいときのHartree-Fockの近似理論が,強磁場の下でも成立することを示したもので,中性子星等の理論への応用が期待される. 中性子星の表面は主に鉄原子で占められており,重力崩壊の為1012〜1013Gまたはそれ以上のオーダーの強い磁場が存在すると予想されている.この表面の状態の数学的な研究としては,Lieb,Solovej,Yngvason等によるものが有り,クーロン力で相互作用する多体電子系の最低固有エネルギーの強磁場及び多体極限での漸近挙動として定式化された.その結果によれば,磁場の強さBと核の電荷Zとの相互関係によって以下の5通りに場合分けできる(1)B≪Z4/3;(2)B〜Z4/3;(3)Z4/3≪B≪Z3;(4)B〜Z3;(5)Z3≪B.彼らは,それぞれの領域で妥当な近似理論を展開し,最低固有エネルギーの漸近挙動を調べた.本論文では,これらのいずれの場合に於いてもHartree-Fock近似が適用できること,しかも上で使われた近似理論よりもHartree-Fock近似の方が誤差が小さいことなどがしめされている. 第2部の第1章は,上の(3)〜(5)の領域で成り立つDensity matrix theoryを分子モデルに拡張した場合の結果が与えられている.ここで考察されるハミルトニアンは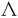 NL2(R3;C2)上の NL2(R3;C2)上の であり,ここにA(x)=B×xはx3方向の定磁場B>0に対応するベクトルポテンシャル,はK個の核(電荷Zj>0)によるクーロンポテンシャルである.この最低固有エネルギーE(N,{Zj},B)は,正規化された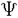 をHNの定義域内で動かしたときの( をHNの定義域内で動かしたときの(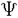 ,HN ,HN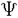 )の下限であり,問題はこの量のZj=kjZと置きN/Z>0を固定してB=O(Za)という関係を保ちながらZ→∞としたときの挙動を求めることである.まずZ4/3≪Bのとき,全ての電子は漸近的に最低ランダウバンドにあるとしてよいことが示される.すなわち,最低ランダウバンドの空間内での( )の下限であり,問題はこの量のZj=kjZと置きN/Z>0を固定してB=O(Za)という関係を保ちながらZ→∞としたときの挙動を求めることである.まずZ4/3≪Bのとき,全ての電子は漸近的に最低ランダウバンドにあるとしてよいことが示される.すなわち,最低ランダウバンドの空間内での(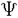 ,HN ,HN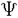 )の下限として定義されるEconf(N,{Zj},B)がZ4/3≪Bのときlimz→∞ Econf(N,{Zj},B)/E(N,{Zj},B)=1を満たすことが示される. )の下限として定義されるEconf(N,{Zj},B)がZ4/3≪Bのときlimz→∞ Econf(N,{Zj},B)/E(N,{Zj},B)=1を満たすことが示される. 次にこのエネルギーをDensity matrixの汎関数で近似したものの最小化問題の解としてEDM(N,{Zj},B)という量が導入され,これに対してZ4/3≪Bのときlimz→∞EDM(N,{Zj},B)/Econf(N,{Zj},B)=1が示される. 第2章では,Hartree-Fock近似を用いて同じ問題が調べられ,続いて上述の比較的考察がなされている.Hartree-FockエネルギーをSlater行列式で表された波動関数の中での最低固有エネルギー として定義し,このEuler-Lagrange方程式としてHartree-Fock方程式を導き,その解の存在と一意性,指数型減衰などが示された後,B=O(Za)(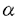 >0)のときlimz→∞EH(N,{Zj},B)/E(N,{Zj},B)=1が証明されている. >0)のときlimz→∞EH(N,{Zj},B)/E(N,{Zj},B)=1が証明されている. 第3章では,(1)〜(3)に現れるMagnetic Thomas-Fermi theoryで求められたエネルギーの(絶対温度零での)熱力学的極限が考察されている. 以上のような内容は磁場中のSchrodinger方程式の解析においていくつかの興味深い新しい数学的結果を与えたものであり,扱われた設定は物理的にも意味のあるものである.このような問題における数学的厳密化は往々にして非常に困難であるので,本論文提出者 中野史彦 は,博士(数理科学)の学位を受けるにふさわしい十分な資格があるものと認める. |