| 内容要旨 | | Dを向き付けられた3つ穴のあいた2次元球面とする。この論文の主たる内容は、D上のSU(3)-平坦接続のモジュライ空間の存在条件を決定し、この条件と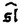 (3;C)フュージョンルールを比較する事により、フュージョンルールに関する新しい結果を得ることである。得られた条件はフュージョン係数が消えないための必要条件であり一群の不等式を用いて記述されるが、フュージョンルールに関する条件の中でも最も簡単な記述の一つになっている。この不等式に於ける等号を一つでも満たすような最高ウェイトの重複度は1でなければならないことも示した。これはPRV-予想の量子化版と考えられるが、モジュライ空間がCP1か1点に位相同型であることから導かれる。 (3;C)フュージョンルールを比較する事により、フュージョンルールに関する新しい結果を得ることである。得られた条件はフュージョン係数が消えないための必要条件であり一群の不等式を用いて記述されるが、フュージョンルールに関する条件の中でも最も簡単な記述の一つになっている。この不等式に於ける等号を一つでも満たすような最高ウェイトの重複度は1でなければならないことも示した。これはPRV-予想の量子化版と考えられるが、モジュライ空間がCP1か1点に位相同型であることから導かれる。 G=SU(3)とする。TをGの標準的極大トーラスとして固定すると、Gの共役類の空間G/AdGはt=Lie(T)内の三角形領域 と同一視される。共役類の三つ組 と同一視される。共役類の三つ組 =( =(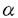 , ,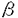 , ,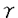 )∈ )∈ 3を一つ固定し、 3を一つ固定し、 に付随したD上のSU(3)-平坦接続のモジュライ空間 に付随したD上のSU(3)-平坦接続のモジュライ空間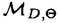 を考える。このモジュライ空間の存在条件は、 を考える。このモジュライ空間の存在条件は、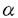 , ,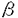 , ,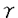 の成分を用いて次のように記述される。 の成分を用いて次のように記述される。 定理A(定理4.3).三つ組 =( =(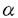 , ,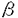 , ,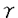 )に対して、 )に対して、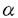 =( =(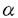 1, 1,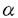 2, 2,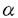 3), 3),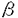 =( =(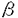 1, 1,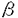 2, 2,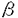 3), 3),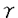 =( =(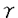 1, 1,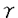 2, 2,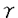 3)と書く。このとき、モジュライ空間 3)と書く。このとき、モジュライ空間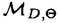 が空集合とならないための必要十分条件は、 が空集合とならないための必要十分条件は、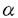 , ,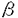 , ,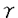 が次の18本の不等式全てを満たすことである。 が次の18本の不等式全てを満たすことである。 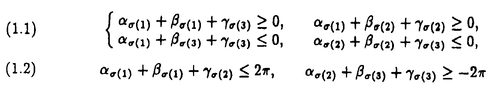 但し、ここに於いて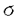 ∈Z/3Zは各不等式の左辺 ∈Z/3Zは各不等式の左辺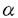 i+ i+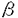 j+ j+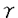 kの添え字集合{i,j,k}に対してそのサイクリックな入れ替えとして作用する。 kの添え字集合{i,j,k}に対してそのサイクリックな入れ替えとして作用する。 この条件は、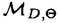 を定める方程式から定義される写像 を定める方程式から定義される写像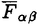 :T\G/T→ :T\G/T→ を調べることにより求められる。この写像は、あるモーメント写像から導かれるものと考えられ、その像は を調べることにより求められる。この写像は、あるモーメント写像から導かれるものと考えられ、その像は 内の多角形領域となる。この領域をQ=Q( 内の多角形領域となる。この領域をQ=Q(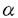 , ,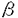 )と書く。最も一般的な場合、Qは六角形となる。定理Aの(1.1),(1.2)で与えられた条件は )と書く。最も一般的な場合、Qは六角形となる。定理Aの(1.1),(1.2)で与えられた条件は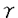 *=(- *=(-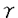 3,- 3,-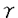 2,- 2,-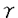 1)がQに含まれることと同値である。また、 1)がQに含まれることと同値である。また、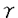 *の逆像 *の逆像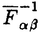 ( (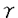 *)を調べることにより、モジュライ空間 *)を調べることにより、モジュライ空間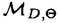 の位相型を決定することが出来る。 の位相型を決定することが出来る。 定理B(定理4.6).三つ組 =( =(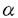 , ,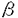 , ,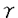 )は定理Aに於ける全ての不等式を満たしているとする。このとき、モジュライ空間 )は定理Aに於ける全ての不等式を満たしているとする。このとき、モジュライ空間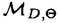 はCP1または1点に同相である。より正確には、 はCP1または1点に同相である。より正確には、 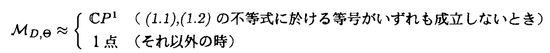 となる。 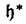 をsl(3;C)の双対カルタン部分環とする。レベルと呼ばれる正整数Kを固定し、P+(3;K)⊂ をsl(3;C)の双対カルタン部分環とする。レベルと呼ばれる正整数Kを固定し、P+(3;K)⊂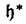 をレベルKドミナント整ウェイトの集合と考える。P+(3;K)を包絡する をレベルKドミナント整ウェイトの集合と考える。P+(3;K)を包絡する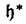 の三角形領域 の三角形領域 *(アルコーブと呼ばれる)はアフィンワイル群 *(アルコーブと呼ばれる)はアフィンワイル群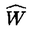 の作用に関する基本領域と考えられ、 の作用に関する基本領域と考えられ、 との間に との間に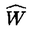 のこの作用と両立する自然な同型写像f: のこの作用と両立する自然な同型写像f: 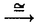  *を構成することが出来る。この同一視の下で *を構成することが出来る。この同一視の下で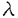 =f( =f(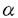 ), ),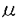 =f( =f(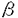 ), ),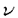 =f( =f(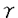 )とおくと、定理Aで与えられた条件は )とおくと、定理Aで与えられた条件は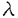 , ,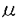 , ,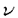 を用いて書き直すことが出来る(系5.2)。Q=Q( を用いて書き直すことが出来る(系5.2)。Q=Q(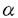 , ,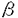 )に対応する領域をQ*=Q*( )に対応する領域をQ*=Q*(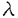 , ,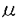 )とする。一方、[KMSW]に拠れば )とする。一方、[KMSW]に拠れば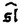 (3;C)フュージョンルールは、Berenstein-Zelevinsky三角形を用いることによって完全に記述されている。系5.2の結果をこれと比較すると次の定理を得る。 (3;C)フュージョンルールは、Berenstein-Zelevinsky三角形を用いることによって完全に記述されている。系5.2の結果をこれと比較すると次の定理を得る。 定理C(定理5.4).もし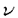 がQ*=Q*( がQ*=Q*(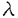 , ,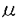 )に含まれなければ、フュージョン係数 )に含まれなければ、フュージョン係数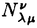 は消える。より具体的には以下のように記述される。 は消える。より具体的には以下のように記述される。 V*=V*(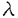 , ,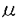 )⊂ )⊂ *を *を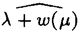 ( (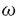 ∈W)全体からなる集合とする。ここで、WはG=SU(3)のTに関する(古典)ワイル群で、 ∈W)全体からなる集合とする。ここで、WはG=SU(3)のTに関する(古典)ワイル群で、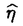 ∈ ∈ *は上で述べた *は上で述べた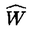 の作用に関する の作用に関する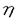 ∈ ∈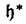 の軌道上の の軌道上の *を通る唯一の点を表す。もし *を通る唯一の点を表す。もし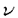 =[ =[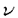 1, 1,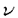 2]が以下の不等式 2]が以下の不等式 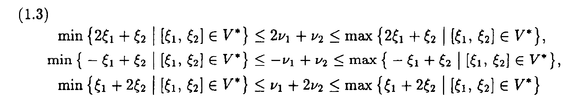 を満たさなければ、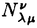 =0となる。 =0となる。 これはフュージョンルールに関する新しい記述法であり、今までに知られているフュージョンルールを与える条件の中でも最も簡単な記述の一つとなっている。この条件は勿論必要条件に過ぎないが、本論分に於いてもいくつかの例をあげたようにQ*=Q*(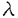 , ,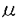 )の頂点に位置する最高ウェイトはフュージョン代数の積 )の頂点に位置する最高ウェイトはフュージョン代数の積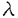 ・ ・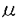 の分解に必ず現れるであろうと期待される。これに関連して、次の定理を示した。 の分解に必ず現れるであろうと期待される。これに関連して、次の定理を示した。 定理D(定理5.5).Q*=Q*(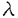 , ,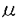 )の境界に現れる )の境界に現れる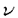 の重複度は の重複度は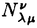 =1である。 =1である。 この結果は、PRV-予想([PRV],[Ku])の量子化版であると考えることが出来る。これは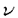 ∈Q*( ∈Q*(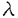 , ,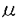 )に対応するモジュライ空間 )に対応するモジュライ空間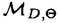 が1点になることに対して、[F],[BL],[KNR]の結果を適用することにより証明される。また、定理Cの系として、フュージョン係数 が1点になることに対して、[F],[BL],[KNR]の結果を適用することにより証明される。また、定理Cの系として、フュージョン係数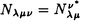 が消えなければ、三つ組 が消えなければ、三つ組 =(f-1( =(f-1(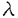 ),f-1( ),f-1(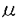 ),f-1( ),f-1(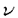 ))∈ ))∈ 3に付随するモジュライ空間 3に付随するモジュライ空間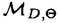 も空集合とはならないことが示される。これは[F],[BL],[KNR]の結果を部分的にではあるが、基本的な道具のみを用いてG=SU(3)の場合について追確認したことになる。 も空集合とはならないことが示される。これは[F],[BL],[KNR]の結果を部分的にではあるが、基本的な道具のみを用いてG=SU(3)の場合について追確認したことになる。 REFERENCES[BL] A.Beauville and Y.Laszlo,Conformal Blocks and Generalized Theta Function,Commun.Math.Phys.164(1994),385-419.[F] G.Faltings,A Proof for the Verlinde Formula,J.Alg.Geom.3(1994),347-374.[KMSW]A.N.Kirillov,P.Mathieu,D.Senechal and M.A.Walton,Can Fusion Coefficients Be Calculated from the Depth Rule?,Nucl.Phys.B391(1993),651-674[KNR] S.Kumar,M.S.Narasimhan and A.Ramanathan,Infinite Grassmannians and Moduli Spaces of G-bundles,Math.Ann.300(1994),41-75.[Ku] S.Kumar,Proof of the Parathasarathy-Rango Rao-Varadarajan conjecture,Invent.Math.93(1988),117-130[PRV] K.R.Parathasarathy,R.Rango Rao and V.S.Varadarajan,Representations of Complex Semisimple Lie Groups and Lie Algebras,Ann.Math.85(1967),383-429 |
| 審査要旨 | | リーマン面上の共形場理論における,共形ブロック空間の次元はVer-linde公式によって与えらる.また,共形ブロックの空間は,幾何学的には,リーマン面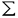 上のG平坦接続のモジュライ空間のケーラー偏極による量子化の空間としてとらえられることが知られている.一方,平坦接続のモジュライ空間 上のG平坦接続のモジュライ空間のケーラー偏極による量子化の空間としてとらえられることが知られている.一方,平坦接続のモジュライ空間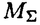 は,シンプレクティック構造をもち,G=SU(2)の場合には,共形ブロックの空間 は,シンプレクティック構造をもち,G=SU(2)の場合には,共形ブロックの空間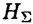 の次元は, の次元は,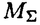 へのトーラス作用に関するモーメント写像の像の格子点の個数によって与えられることが,Jeffery-Weitsmanによって示された. へのトーラス作用に関するモーメント写像の像の格子点の個数によって与えられることが,Jeffery-Weitsmanによって示された. 論文提出者 林正人は,Verlinde公式を,モジュライ空間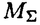 のシンプレクティック幾何の立場からとらえることをテーマとして研究した.具体的には,G=SU(3)の場合について,リーマン面のパンツ分解にあらわれる3つ穴のあいた球面上のG平坦接続のモジュライ空間を調べ,次のような成果を得た.まず,極大トーラスTについて,モーメント写像f:G/T→Cを構成して,モジュライ空間をfの逆像としてとらえ,モジュライ空間が空でないとき,S2または一点になることを示した.また,モーメント写像の像を決定し,モジュライ空間が空でないための必要十分条件を不等式で与えた.さらに,この不等式が,Berenstein-Zelevinsky三角形の存在条件の必要条件であることを示し,Kirillovらの結果とあわせて,モジュライ空間が空ならば,共形ブロックの空間の次元が0となるという事実に関する初等的な証明を得た.さらに,モーメント写像の像の境界の格子点について,対応する共形ブロックの空間が1になることを示した. のシンプレクティック幾何の立場からとらえることをテーマとして研究した.具体的には,G=SU(3)の場合について,リーマン面のパンツ分解にあらわれる3つ穴のあいた球面上のG平坦接続のモジュライ空間を調べ,次のような成果を得た.まず,極大トーラスTについて,モーメント写像f:G/T→Cを構成して,モジュライ空間をfの逆像としてとらえ,モジュライ空間が空でないとき,S2または一点になることを示した.また,モーメント写像の像を決定し,モジュライ空間が空でないための必要十分条件を不等式で与えた.さらに,この不等式が,Berenstein-Zelevinsky三角形の存在条件の必要条件であることを示し,Kirillovらの結果とあわせて,モジュライ空間が空ならば,共形ブロックの空間の次元が0となるという事実に関する初等的な証明を得た.さらに,モーメント写像の像の境界の格子点について,対応する共形ブロックの空間が1になることを示した. 3つ穴のあいた球面の場合,共形ブロックの空間の次元は,fusion代数の構造定数にほかならない.林正人の結果は,SU(3)fusion代数に関して,幾何学的な観点から,新たな知見を与えるものであり,また,共形場理論をシンプレクティック幾何の立場から理解する上で重要なステップを確立するものである.よって,論文提出者 林正人 は,博士(数理科学)の学位を受けるに充分な資格があると認める. |