| 1Smooth Besselization Technique リーマン多様体上の拡散過程について考えよう。特にその半径方向のふるまい、例えば近傍からの脱出時間などを調べたい。多様体上の拡散過程の漸近展開についてはMalliavin解析によって良く調べられているが、従来の枠組では脱出時間のような量は扱いにくい。そこで我々は渡辺信三氏と高橋陽一郎氏によるOnsager-Machlup公式の研究で用いられた、ドリフト変更による確率過程のBessel化の手法を応用することで新たなアプローチを与える。 多様体上のブラウン運動の局所的なふるまいが次の確率微分方程式(S.D.E.)で記述されることはよくしられている。 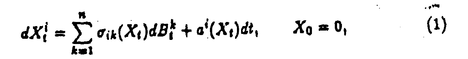 ここで、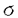 ij(x)はgij(x)のsquare root,i.e., ij(x)はgij(x)のsquare root,i.e.,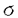 ij(x)は対称で ij(x)は対称で 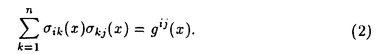 そして、ai(x)はCoriolis drift, 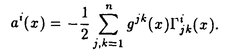 この時、上のS.D.E.に対して、ドリフト項のみを変更したS.D.E.: 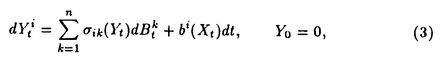 を考えて、この過程のradial part,すなわち‖Yt‖がBessel processになるようにできる。このドリフト変更に対してGirsanov-丸山の公式を用いて、もとの過程の研究をすることができる。 我々の方法のポイントはこのドリフトの新たな取り方の発見である。すなわち、我々はBessel化のドリフトとして性質の良い滑らかなものをとることができる。このことによって確率過程の半径方向が持つsingularityを良く性質のわかっているBessel過程に帰着し、しかもこのずれの現れるGirsanov密度の項もドリフトの滑らかさのおかげで機械的に漸近展開することができるようになる。 以下ではこの方法によって三つの問題を考えていく。 2Joint Distribution of Exit Time and Position from Small Geodesic Balls 確率微分幾何の基本的な問題として、多様体上のBrown運動を通して多様体自身の幾何的な情報を取り出すという問題がある。その局所的な場合には、1980年代からM.A.Pinskyを中心とする研究者達によってBrown運動の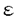 -球からの脱出時間や脱出場所の平均の -球からの脱出時間や脱出場所の平均の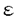 →0での漸近展開の係数に様々な幾何的な量が現れることが研究されている。 →0での漸近展開の係数に様々な幾何的な量が現れることが研究されている。 しかし、彼等の手法は局所座標によるラプラシアンの漸近展開を用いる偏微分方程式の手法によるもので、機械的に計算ができるものの展開係数の現れる意味が全く不明で、確率論の立場としては不満であった。 そこで我々はプロセスのBessel化というアイディアをこの問題に応用して、PinskyとM.Liaoによる脱出場所と脱出時間の結合分布の展開に対して多項式的Wiener汎関数による積分表示を与えた。またこの汎関数の計算を実行して、彼等の展開に完全に確率解析のみを用いた証明を与えることができ、積分表示によって更に詳しい情報を得ることができる。この計算にはBrown運動の回転対称性の利用や、逆向き時間の確率積分の応用などのテクニックが用いられる。 以下では主要な結果をもう少し具体的に述べることにする。 Riemann多様体上のBrown運動の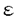 -球からの脱出時間 -球からの脱出時間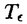 と脱出場所の結合分布について、M.A.PinskyとM.Liaoは次の漸近展開を得ている(cf.Liao[4],Pinsky[5])。 と脱出場所の結合分布について、M.A.PinskyとM.Liaoは次の漸近展開を得ている(cf.Liao[4],Pinsky[5])。 定理2.1 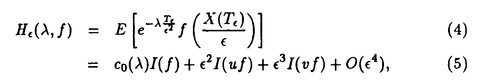 ここにIは単位球面S上の一様分布、uと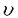 は次のようなS上の関数 は次のようなS上の関数 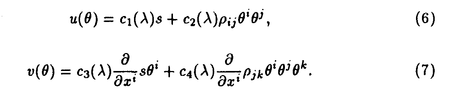 ci(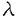 )は )は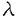 と次元のみによる定数でBessel関数で書けるようなもの。 と次元のみによる定数でBessel関数で書けるようなもの。 また、M.KozakiとY.Oguraも脱出時間と脱出場所の独立性の研究において同様の計算をしていて、この独立性が多様体の族の空間の距離と関係していることを指摘している。(cf.Kozaki-Ogura[3])。 彼らの手法は正規座標でラプラシアンを展開し次数別に偏微分方程式を解くという解析的なものであるが、この方法では漸近展開のもつ確率論的な意味が全くわからない。 そこで我々はY.TakahashiとS.Watanabeによって用いられた"processのBessel化"の手法を応用することで上の展開に対応するパス空間上の展開を与えた(Theorem 2.2)。 ここで用いるBessel化ドリフトはTakahashi-Watanabeでの物と異なって滑らかな性質を持ち、この新しいドリフトの選び方は我々の証明の中で本質的な役割を果たす事を注意しておく。 Theorem2.2の中のWiener Functionalsをexplicitに計算する事ができてPinsky達の展開が得られるのだが、その上、展開の係数ci(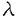 )についてTheorem2.3の表現を得ることができる(Hara[1])。 )についてTheorem2.3の表現を得ることができる(Hara[1])。 定理2.2 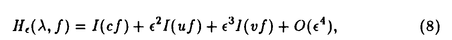 ここにIは単位球面S上の一様分布で、定数c=E[exp(-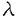 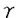 )]、uとvは次のようなWiener Functionals: )]、uとvは次のようなWiener Functionals: 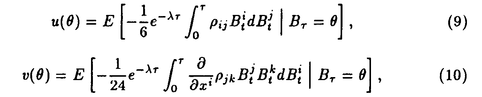 ここに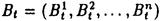 はRnの標準Brown運動で、 はRnの標準Brown運動で、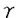 はその単位球からの脱出時間。 はその単位球からの脱出時間。 定理2.3 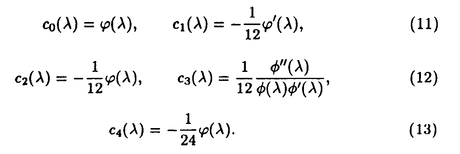 ここに、 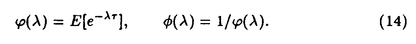 3Parallel Translation for Brownian Motion conditioned to hit a fixed point of a sphere PinskyとLiaoはまた、リーマン多様体上のブラウン運動の経路に沿って測地球からの脱出場所まで確率並行移動したベクトルの漸近展開も計算しているが、この問題に対しても我々の手法を適用できる。すなわち次の定理に滑らかなBessel化による確率論的な証明を与えることができる。この時もドリフトの滑らかな取り方がWiener汎関数の計算において本質的な役割を果たす。 定理3.1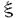 はXtに沿った確率並行移動で、 はXtに沿った確率並行移動で、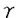 は半径rの測地球からの脱出時間、 は半径rの測地球からの脱出時間、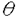 はその球上に点とする時、 はその球上に点とする時、 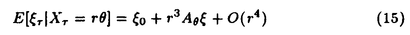 ここに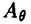 :Rn→Rnは :Rn→Rnは 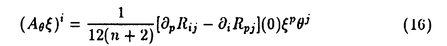 で定義される線型写像で、RijはRicci曲率である。 この確率並行移動の漸近展開については、接ベクトルの並行移動を主バンドルの枠組でとらえなおした同様の展開を考えると、Yang-Mills接続の条件が得られることがS.Staffordによって指摘されている[6]。もちろんこの展開に対しても全く同様に我々の確率論的な手法で証明することができるが、このような確率論的な量の漸近展開からYang-Mills理論に対して新しいアプローチが考えられるかどうかは、これからの課題である。 4 Lagrangian for Pinned Diffusion Process(with Y.Takahashi) リーマン多様体上の拡散過程と固定した曲線を考えよう。渡辺信三氏と高橋陽一郎氏はこの曲線の近傍に拡散過程が滞在する確率の漸近挙動を調べて、いわゆるOnsager-Machlupの公式における曲率の効果を研究した([7])。我々の滑らかなBessel化ドリフトの手法を用いることに依って、Takahashi-Watenabeの証明を著しく簡単化することができる。しかも、[7]の主張を両端を固定したブラウン運動の場合にもほとんど自動的に拡張することができる(with Y.Takahashi[2])。すなわち、次の定理を示す事ができる。 定理4.1ベクトル場fを持つRiemann多様体上のブラウン運動x(t)と滑らかな曲線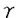 (t), (t),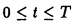 について、次が成立する。 について、次が成立する。 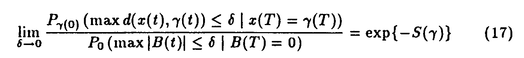 ここにdはRiemannian距離, 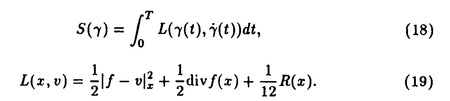 ここで、| |xはxにおける接空間上のRiemannian norm、divはdivergence、R(x)はxにおけるRicci曲率である。 Takahashi-Watanabeにおいてはスカラー曲率の現れるWiener汎関数の項の評価が極めて複雑で、解析的な手法を借りてこざるを得なかった。我々の新しい方法はドリフトのsingularityを除去したことで、すべての部分を確率論的な計算に帰着させることができる。また、このことによって半径方向の条件づけをおこなうことがほとんど自動的に可能になり、上記の定理のような拡張ができるということを注意しておく。 References[1]K.Hara:Wiener functionals associated with joint distributions of exit time and position from small geodesic balls,Ann.Probab.,to appear.[2]K.Hara and Y.Takahashi:Lagarangean for pinned diffusion process,Ito’s Stochastic Calculus and Probabilistic Theory,Springer-Verlag,to appear.[3]M.Kozaki and Y.Ogura:On the independence of exit time and exit position from small geodesic balls for Brownian motions on Riemannian manifolds,Math.Z.,197(1988),561-581.[4]M.Liao:Hitting distrbutions of small geodesic spheres,Ann.Probab.,16(1988),1039-1050.[5]M.A.Pinsky:Local stochastic differential geometry or What can you learn about a manifold by watching Brounian motion?,Contemporary Math.,73(1988),263-272.[6]S.Stafford:A Stochastic Criterion for Yang-Mills Connections,Diffusion Processes and Related Problems in Analysis,vol.1(1990),Ed.M.A.Pinsky,Birkhauser,313-322[7]Y.Takahashi and S.Watanabe:The probability functionals(Onsager-Machlup functions)of diffusion processes,Proc.L.M.S.Simp.on Stochastic Integrals at Durham,Lecture note in Math 851(1980),Springer,433-463 |