| 内容要旨 | | 整型(又は実解析的)範疇のGoursat問題には幾つかの研究が成されており,特にC.Wagschalはこの問題を積分-微分方程式系に拡張し,Cauchy-Kovalevskaja型定理(即ち一意可解性定理)を示している.併し乍ら,超局所解析に於いてはGoursat問題の研究は現在の所見当たらない様である.そこでこの論文では,多変数Fuchs型超局所微分作用素(microdifferential operator)に依る整型函数及び超局所函数(microfunction)の枠内のGoursat問題を考察する. (一つの変数に関する)Fuchs型の概念は先づ偏微分作用素の場合にM.S.Baouendi-C.Goulaouicに依って導入され,又Cauchy-Kovalevskaja型定理も示された.これに続いてN.S.MadiはFuchs型作用素を多変数に拡張し整型函数に於けるGoursat問題のCauchy-Kovalevshja型定理を証明した. 一方Baouendi-Goulaouicに引き続き,多くの数学者に依りFuchs型作用素に対して初期値問題のほぼ満足すべき結果が得られている.例えば田原はVolevicの意味のFuchs系を扱い,複素領域に於いてCauchy-Kovalevskaja型定理を示した.彼はその超局所解析への応用として,"Fuchs型双曲系"の仮定下で佐藤超函数(Sato hyperfunction,以下単に超函数と呼ぶ)の枠内での初期値問題の一意可解性を示し,その応用として柏原-河合の方法の延長に依り,超局所微分作用素の"Fuchs型超局所双曲系"に対し超局所函数の枠内での斉次初期値問題の可解性定理を証明した.更に大阿久はFuchs型双曲型超局所微分作用素に対して超局所函数の枠内での非斉次初期値問題の可解性定理を証明し,又Fuchs型超局所微分作用素に対してF-mildの仮定下で一意性を示した. そこでこの論文では上の結果の自然な拡張として,多変数Fuchs型超局所微分作用素を定義し,超局所微分作用素の整型函数に対するBony-Schapiraの作用を用いてGoursat問題のCauchy-Kovalevskaja型定理を示す.更に応用として,作用素に対する或る種の双曲型に類似する条件の下で初期値が充分"滑らか"な場合に,超局所函数の枠内でのGoursat問題の可解性を示す. 以下定理を精確に述べる為,記号を幾つか準備する. Nを正の整数全体の集合とし,N0:=N∪{0}とする.d,n∈Nに対して,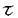 =( =(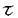 1,…, 1,…,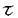 d)∈Cd,z=(z1,…,zn)∈Cnなる座標を用いる事とする.又,一般に集合Dで定義された整型函数の全体の集合を d)∈Cd,z=(z1,…,zn)∈Cnなる座標を用いる事とする.又,一般に集合Dで定義された整型函数の全体の集合を (D)で表す. (D)で表す.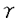 =( =(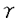 1,…, 1,…,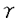 d)∈Rdに対して[ d)∈Rdに対して[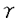 ]+:=([ ]+:=([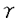 1]+,…,[ 1]+,…,[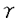 d]+)([ d]+)([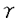 j]+:=max{ j]+:=max{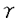 j,0})と置く.m=(m1,…,md), j,0})と置く.m=(m1,…,md),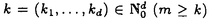 を固定する.R=(R1,…,Rd)∈Rdに対してB(R):={ を固定する.R=(R1,…,Rd)∈Rdに対してB(R):={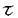 ∈Cd;| ∈Cd;|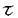 j|<Rj(1 j|<Rj(1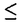 j j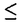 d)}とする.V⊂Cnを原点の相対compact開近傍とし,正数h0に対してU={(z, d)}とする.V⊂Cnを原点の相対compact開近傍とし,正数h0に対してU={(z,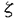 )∈T*Cn;z∈V, )∈T*Cn;z∈V,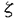 1=1,| 1=1,|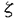 j|<h0(2 j|<h0(2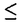 j j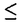 n)}と置く. n)}と置く. 定義.[U]×[B(R)]([ ]は閉包を表す)の近傍で定義された|m|階超局所微分作用素P(z,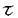 ; ;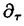 ,∂z)が重み(k,m)のFuchs型とは ,∂z)が重み(k,m)のFuchs型とは 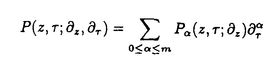 の形であって以下の条件を満たす事と定義する: (1)各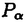 は は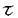 を整型助変数に持つ; を整型助変数に持つ; (2)各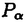 は は 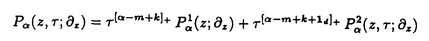 の形であり (2-1)Pm=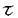 k; k; (2-2)ord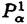 (z;∂z) (z;∂z)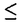 0; 0; を満たす.但し1d:=(1,…,1)∈Ndとする. 上の定義に於いて,Fuchs型という概念はz変数の座標変換,より一般に(z;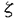 )変数の被量子化接触変換(quantized contact transform)で不変である事に注意する. )変数の被量子化接触変換(quantized contact transform)で不変である事に注意する. T=(T1,…,Td)をd個の不定元とする.Pが重み(k,m)のFuchs型の時その決定多項式(indicial polynomial)を 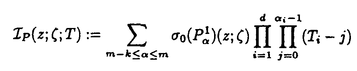 で定義する(但し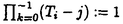 とする). とする). 注意.d=1ならば,上のFuchs型の定義は田原に依り導入されたFuchs型に一致し更に一般のdに対してはMadiの意味のFuchs型偏微分作用素の自然な拡張となっている. A(z,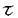 ;∂z)を[U]×[B(R)]の近傍で定義された ;∂z)を[U]×[B(R)]の近傍で定義された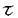 を整型助変数に持つ有限階超局所微分作用素とする.或るc∈Cを取り を整型助変数に持つ有限階超局所微分作用素とする.或るc∈Cを取り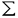 :={z∈Cn;z1=c}とする.次に開凸集合 :={z∈Cn;z1=c}とする.次に開凸集合 ⊂VがBony-Schapiraの意味でh0- ⊂VがBony-Schapiraの意味でh0-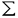 -平坦とする.即ち,Vはz∈ -平坦とする.即ち,Vはz∈ ,w∈ ,w∈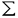 且つh0|zj-wj| 且つh0|zj-wj|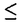 |z1-w1|(j=2,…,n)ならばw∈ |z1-w1|(j=2,…,n)ならばw∈ ∩ ∩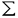 を満たす集合とする.この時,任意の を満たす集合とする.この時,任意の ×B(R)上の整型函数f(z, ×B(R)上の整型函数f(z,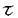 )に対してBony-Schapiraの議論が適用出来て,整型助変数付きの超局所微分作用素の整型函数への作用 )に対してBony-Schapiraの議論が適用出来て,整型助変数付きの超局所微分作用素の整型函数への作用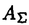 f(z, f(z,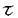 )∈ )∈ ( ( ×B(R))がwell-definedが従う.z0∈ ×B(R))がwell-definedが従う.z0∈ ∩ ∩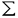 を固定し を固定し 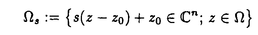 と置く.次の条件を考える. [A-1].或る定数C>0と[U]の近傍Wとが存在して任意の(z;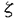 )∈[W]及び )∈[W]及び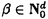 ( (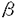 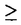 m-k)に対して m-k)に対して 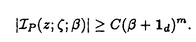 定理.[A-1]を仮定する.この時,或る定数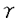 0>0が存在して次が成り立つ: 0>0が存在して次が成り立つ: 0<h<h0及び0<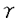 < <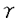 0を任意に選ぶ. 0を任意に選ぶ. をh- をh-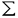 -平坦なVの開凸な部分集合であってdia -平坦なVの開凸な部分集合であってdia 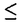 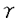 を満たすとする(但しdiaは直径を表す).この時或る定数 を満たすとする(但しdiaは直径を表す).この時或る定数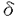 (P及び (P及び のみに依存する)が存在して次を満たす:任意の のみに依存する)が存在して次を満たす:任意の ×B(R)上の整型函数f(z, ×B(R)上の整型函数f(z,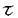 ),g(z, ),g(z,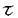 )に対してGoursat問題 )に対してGoursat問題 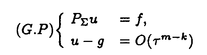 の整型函数解u(z,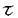 )が一意に存在して(少なくとも) )が一意に存在して(少なくとも) 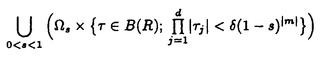 で整型となる. 注意.Pが微分作用素の時,上の定理はMadiに依って得られている. この定理を超局所解析に応用する.以下簡単の為d=2と仮定する.M:=Rn×R2={(x,t)}その複素化をX:=Cn×C2=Y×C2={(z,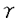 )}.とし,更にN:=Rn={x∈Rn} )}.とし,更にN:=Rn={x∈Rn}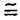 M∩{t=0} M∩{t=0}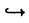 M,L:=X∩{Imz=0}=Rn×C2, M,L:=X∩{Imz=0}=Rn×C2,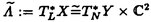 , ,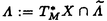 と夫々置く. と夫々置く.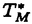 X(resp. X(resp.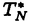 Y)上の超局所函数の層を通常の様に Y)上の超局所函数の層を通常の様に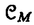 (resp. (resp.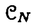 )と書き,更に )と書き,更に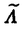 上の整型助変数付き超局所函数の層を 上の整型助変数付き超局所函数の層を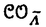 とする. とする.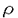 を を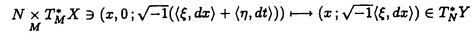 なる自然写像とすると規準的に次がある; なる自然写像とすると規準的に次がある; 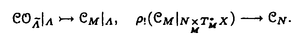 p0:=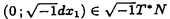 としP(x,t;∂x,∂t)を としP(x,t;∂x,∂t)を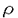 -1(p0)の近傍に於ける重み(m,k)のFuchs型超局所微分作用素とする.この時 -1(p0)の近傍に於ける重み(m,k)のFuchs型超局所微分作用素とする.この時 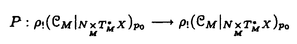 が誘導される.Pの主表象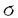 |m|(P)に対して次の条件を考える: |m|(P)に対して次の条件を考える: [A-2].或る函数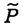 が存在し が存在し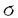 |m|(P)(z, |m|(P)(z,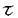 ; ;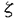 , ,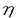 )= )=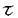 k k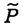 (z, (z,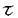 ; ;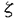 , ,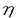 )と書け )と書け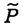 は次の条件を満たす: は次の条件を満たす: 或る正定数h0,Mが存在して集合 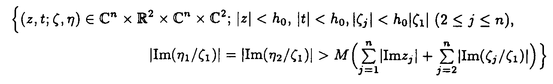 上で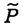 (z,t; (z,t;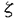 , ,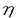 )は零にならぬ. )は零にならぬ. 定理.[A-1]と[A-2]とを仮定する.この時,任意の整型助変数付き超局所函数 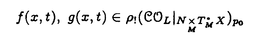 に対してGoursat問題 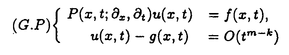 の超局所函数解 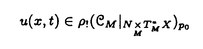 が存在する. 系.Pは解析的微分作用素であり[A-1]及び次を仮定する; 或るPj(j=1,2)が存在して 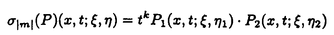 と書けPjは各々tj方向に双曲型である. この時,任意の整型助変数付き超函数 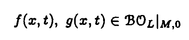 に対してGoursat問題 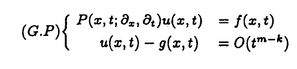 の超函数解 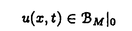 でtを実解析的助変数に持つものが存在する. |