| 内容要旨 | | 1.研究の背景、筆者の研究対象 1960年代、高次元(n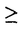 5)のPoincare予想が解決された時に使われた手法の一つに、Whitney’s trickというものがあった。これは、多様体内で部分多様体が数ヵ所の交点で交わっている時、その交点を2つ一組で連続的変形で解消する、というものである。ここで、各交点には符号が定義されることに注意する。解消されるのは互いに異符号の2交点である。低次元ではこの手法が高次元の様には働かない。そこで4次元多様体のトポロジーは1980年代以来、固有の手法で発展してきた。 5)のPoincare予想が解決された時に使われた手法の一つに、Whitney’s trickというものがあった。これは、多様体内で部分多様体が数ヵ所の交点で交わっている時、その交点を2つ一組で連続的変形で解消する、というものである。ここで、各交点には符号が定義されることに注意する。解消されるのは互いに異符号の2交点である。低次元ではこの手法が高次元の様には働かない。そこで4次元多様体のトポロジーは1980年代以来、固有の手法で発展してきた。 この様な流れの中で、筆者が注目した研究対象は4次元多様体内の曲面である。4次元多様体を調べる上で、曲面達の交差は最重要な鍵である。加えて1994年に解決されたThom予想のような、曲面の埋め込み実現の問題、また結び目理論の拡張としての興味もあった。Whitney’s trickが低次元でうまく働かないことはその双方に関係する。4次元の固有の公式([KeM]等)は、4次元多様体内の曲面の交差に関して、2つの交点が異符号であっても連続変形で解消できない場合があることを示している。すなわち、代数的交点数と幾何的交点数の間に本質的な差がある。代数的交点数はホモロジー上の交差形式をみればよい。幾何的交点数の方はそれ自体、扱われた事も、公式として登場したこともあまりないように思う。本論文の第I論文は、それへの一つの基礎的試みとして捉えられたい。 筆者はまた一貫して、向き付け不可能曲面を積極的に研究対象としている。それは次の様な事実に始まる。 事実2([Wh]):向き付け不可能曲面をR4に埋め込む時、自己交差数は埋め込みに対して整数値で定まり、その値はあるmod4の公式を満たす。 Typeset by AMS-TEX 向き付け不可能曲面を扱う時にしばしば代数的情報がmod2されて情報が落ちてしまうことを思えば、少々不思議な事実と言えるであろう。 筆者は本研究科修士論文においてこの事実のある拡張を、4次元多様体論固有の定理(C.T.C.Wallの定理([Wa]))を利用して幾何的に示した。その英訳公表版が参考論文3-1である。 向き付け不可能曲面を積極的に扱うところから、一方ではS4内のRP2の問題から派生してS4の等分割の着想に至る(参考論文3-2,3)。一方では概複素4次元多様体内の閉曲面の複素点に関するある公式の交差理論による証明に着目した(第II論文)。 2.本論文の内容2-I.第I論文 題目:EN内の超平面の集合の分割とはめ込まれた多様体と超平面の幾何的交点数 ENを、通常のアフィン構造を備えたN次元ユークリッド空間とする。我々は、EN内にはめ込まれた一般次元の閉多様体とその余次元の次元の超平面との幾何的交点数に興味をもつ。 まず、我々の研究対象となる幾つかの空間を説明する。0<n<Nの自然数nに対し、P(N,n)を、EN内のn次元の向き付けられた(以下、有向という)超平面全体のなす集合とする。P(N,n)は(n+1)(N-n)次元の有向多様体となる。実際、これはグラスマン多様体G(N,n)上の階数(N-n)の実ベクトル束の全空間である。次に、0<n1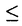 n2<Nをみたす自然数に対し、P(N;n1,n2)を、次の空間とする。 n2<Nをみたす自然数に対し、P(N;n1,n2)を、次の空間とする。 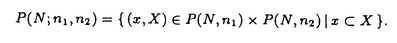 P(N;n1,n2)も有向多様体となる。P(N;n1,n2)からP(N;n1),P(N;n2)へ、それぞれ自然なファイバー写像P1,P2が存在する。 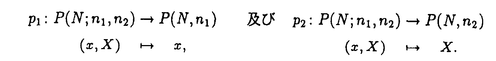 さて、f: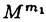 →ENを、m1次元連結閉多様体の滑らかなはめ込みとする。Mは向き付け不可能でもよい。以下ではm2と書いてその余次元N-m1のこととする。我々は、このはめ込みfから上記の二つのファイバー写像を経由して(m2+1)m1-1次元の有向多様体E( →ENを、m1次元連結閉多様体の滑らかなはめ込みとする。Mは向き付け不可能でもよい。以下ではm2と書いてその余次元N-m1のこととする。我々は、このはめ込みfから上記の二つのファイバー写像を経由して(m2+1)m1-1次元の有向多様体E(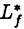 (p1))と、そこからP(N;m2)への連続写像HLfを構成する。HLfの余次元は1であるから、その像はP(N,m2)をいくつかの領域に分割する。像がもつ向きを利用して、P(N,m2)のEndに基点x0をとり、交差理論を利用して各領域に整数を対応させる。これをInt(ImHLf, (p1))と、そこからP(N;m2)への連続写像HLfを構成する。HLfの余次元は1であるから、その像はP(N,m2)をいくつかの領域に分割する。像がもつ向きを利用して、P(N,m2)のEndに基点x0をとり、交差理論を利用して各領域に整数を対応させる。これをInt(ImHLf,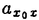 )と書く、但し、xはその領域内の点で、 )と書く、但し、xはその領域内の点で、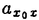 はx0からxへ向かう曲線(Well-definedness等は本文参照のこと)。 はx0からxへ向かう曲線(Well-definedness等は本文参照のこと)。 一方で、点x∈P(N,m2)\ImHLfは、あるEN内のm2次元有向超平面と対応しているが、この時、次が成り立つ。 主定理:上の状況で 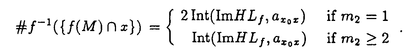 fが埋め込みであるとき、左辺は超平面xとf(M)の幾何的な交点数に一致する。 2-II.第II論文 題目:概複素4次元多様体内の曲面の複素点の個数について (M,J)を実4次元概複素多様体とし、Fを連結閉曲面とする。Fは向き付け不可能でもよい。"一般的な"はめ込みf:F→(M,J)について、Fの点xが複素点であるとは次が成り立つことである([Bi])f*TxF=J(f*TxF)。"一般的な"はめ込みに対しては、各複素点は孤立している(そう定義する)。C(f)と書いてfの複素点全体とする。さて、C(f)の代数的個数に関して、S.M.Websterは次の公式が成り立つことをべクトル場の零点を比較することによって示した。 定理(Websterの公式[We1,2]):上のような状況の下、次が成り立つ。 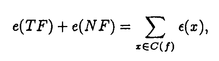 ここで、e(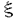 )はベクトル束 )はベクトル束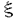 のnormal Euler number(整数値)、 のnormal Euler number(整数値)、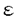 (x)は、各複素点に対して定義される符号(±1)。 (x)は、各複素点に対して定義される符号(±1)。 筆者はこの公式を、交差理論を利用してC2内の有向閉曲面の場合に証明した論文([BF])を再考し、その手法を一般の場合まで補完するため、座標変換で何が生じるか、Fが向き付け不可能な場合(mod2不要)はどう扱えばよいか、という2点について考察した。 この研究のきっかけは、佐伯修氏から([IO])等を紹介され、次の指摘を頂いたことである:参考論文3-1の公式との併用で、Totally Realな向き付け不可能曲面についてのある条件が現われる。 3.参考論文3-1.題目:An Extension of Whitney’s Congruence. (Osaka J.Math.32(1995),185-192掲載)本要旨の1節途中で既に説明した。 3-2.題目:Decomposition of S4 as a twisted double of a certain manifold.(Tokyo J.Math.19 No.2掲載予定) S4が、RP2上の自己交差数2のD2束の全空間を境界で貼り合わせて得られる(等分割)ことは良く知られている([La]等)。この事実がRP2の代わりにある2複体へ一般化されることを示した。これは、S3のHeegaard分解の概念の類似である一方、この次元の位相的グラフ理論の出発点でもある。また、この時境界に現れる3次元多様体がSeifert有理ホモロジー球面であることも指摘。筆者はこの多様体を、S4に埋め込める素な多様体として最も基本的な例であると考えている。また、その2複体に沿うS4の分岐被覆についても考察した。Fermat型代数曲面内に現われる、ある特異ファイバーの近傍と同相になる。等分割を再び貼り直して別の(?)多様体を構成するという問の指摘も数人より頂いている。 筆者はこの論文ではFramed Linkを活用した。これは結び目を利用して個々の4次元多様体を具体的に記述する技法である。具体例が漸く増えてきた4次元多様体論にとって、この技法は今後も役立つと思われる。 3-3.題目:Some Seifert 3-manifolds which decompose S4 as a twisted double. Seifert多様体がS4を等分割する例を可算無限個構成した。その中の、有理ホモロジー球面達について、Casson-Walker不変量がDedekind sumの項を含まない簡単な数列で表されることを示した。 References[Bi] E.Bishop,Differentiable Manifolds in Complex Euclidean Space,Duke.Math.J.32(1965),1-25.[BF] T.Banchoff and F.Farris,Tangential and Normal Euler Numbers,Complex points,and Singularities of Projections for Oriented Surface,Pacific J.Math.161 no.1(1993),1-24.[KeM] M.Kervaire & J.Milnor,On 2-spheres in 4-manifolds,Proc.Nat.Acad.Science USA 47(1961),1651-1657.[IO] G.Ishikawa and T.Ohmoto,Local Invariants of Singular Surfaces in an Almost Complex Four Manifold,Ann.of Global Analysis and Geometry 11(1993),125-133.[La] T.Lawson,Splitting S(4)on RP(2)via the branched cover of CP(2)over S(4),Proc.Amer Math.Soc.86(1982),no.2,328-330[Wa] C.T.C.Wall,Diffeomorphisms of 4-manifolds,J.London Math.Sci.39(1964),131-140.[We1] S.M.Webster,Minimal surfaces in a Kahler surface,J.Diff.Geo.20(1984),463-470.[We2] _,The Euler and Pontrjagin and Numbers of an n-Manifold in Cn,Comm.Math.Helv.60(1985),193-216.[Wh] H.Whitney,Lectures in Topology,University of Michigan Press,1941,pp.101-141. |
| 審査要旨 | | 幾何学的トポロジーにおいて,部分多様体の間の交わりを調べることがしばしば重要な役割を果たす.突き詰めて言えば,トポロジーの重要な不変量のほとんど全てのものは,2つの部分多様体の間の交わりの様子を別の言葉で表現したものにほかならない.偶数次元多様体の符号数も,バンドルの特性類も,皆然りである. 今,N次元多様体にはめ込まれたコンパクトなm1次元多様体M1とN-m1次元多様体M2の間の交点数を調べようとするとき,2つの数え方が区別されるひとつは幾何学的交点数と呼ばれるべきもので,M1とM2が横断的に交わるとして,有限点集合の数(濃度)#(M1∩M2)(∈N∪{0})を数えるもの,もうひとつは全体の多様体とM1,それにM2の全てに向きを与えておき,ホモロジー類[M1]と[M2]の間のホモロジカルな交点数[M1]・[M2](∈Z)を求めるものである.これは代数的交点数と呼ばれるべきものである.はじめに述べたことをより正確に言うと,トポロジーの重要な不変量のほとんどすべてのものは代数的交点数が形を変えたものである. 一方,幾何学的交点数は,重要な不変量に形を変えて現れることは少ないが,しかしその分だけ,通常のトポロジーの不変量を用いては記述しにくい.この事実が,低次元多様体の研究を,高次元多様体のそれに比して困難なものにしている原因である. 山田裕一氏の提出した論文「はめ込みと交差,分割のトポロジー」は二部に分かれている.第一部は「EN内の超平面の集合の分割と,はめ込まれた多様体と超平面の幾何学的交点数」と題され,幾何学的交点数の問題をあつかっている.第二部は「概複素4次元多様体内の曲面の複素点の個数について」と題され,曲面の複素点の個数をその曲面の接束と法束のオイラー類で与えるWebsterの公式の,幾何学的トポロジーによる別証明を与えている. 第一部では,N次元ユークリッド空間ENにはめ込まれたm1次元多様体MとN-m1次元超平面の間の幾何学的交点数をある種の配位空間のなかの代数的交点数を用いて記述する興味深い公式を証明している. 簡単のため,m2=N-m1とおく.EN内の(必ずしも原点を通過しない)m2次元超平面の全体は(m2+1)m1次元の多様体P(N,m2)をなす.MからENへのはめ込みf:M→ENが与えられたとき,f(M)上の1点を通り,その点でMに接する0でない接ベクトルを少なくとも1本含むm2次元超平面の作る部分空間(⊂P(N,m2))をImHLfと表す.(この記号は,提出された論文中の議論の都合による.)大切な観察は,初めの多様体Mが向き付け可能か否かを問わず,ImHLFは,ある自然に向きの付いた多様体のはめ込み像になっていることである.第一論文の主定理は次のように述べることが出来る: 定理:はめ込まれた多様体f(M)とm2次元超平面x(∈P(N,m2)\ImHLf)との間の幾何学的交点数#f-1(f(M)∩x)はつぎの公式で与えられる. ここに,x0はP(N,m2)のエンドに近い一般の点,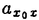 はx0からxへ向かう曲線,そして,Int(ImHLf, はx0からxへ向かう曲線,そして,Int(ImHLf,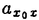 )は配位空間P(N,m2)の中の,ImHLfと )は配位空間P(N,m2)の中の,ImHLfと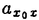 の間の代数的交点数である. の間の代数的交点数である. この定理の証明は配位空間上に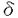 関数とへヴィサイド関数を係数に持つ微分形式を作りそれについてのStokesの公式の両辺をホモロジカルに解釈するという巧妙な方法でなされている.この公式の興味深い点は,従来,トポロジーの不変量を用いては評価しにくかった幾何学的交点数に,初めて,代数的交点数による表現を与えたことである. 関数とへヴィサイド関数を係数に持つ微分形式を作りそれについてのStokesの公式の両辺をホモロジカルに解釈するという巧妙な方法でなされている.この公式の興味深い点は,従来,トポロジーの不変量を用いては評価しにくかった幾何学的交点数に,初めて,代数的交点数による表現を与えたことである. また,幾何学的交点数は,共通部分M1∩M2のオイラー数としても解釈可能であり,そのように解釈すれば,M1∩M2の次元が必ずしも0でない場合への拡張の可能性を含んだ公式とも考えられる. 第二論文におけるWebsterの公式の別証明は,C2の中の有向閉曲面Fという状況でのBanchoffとFarrisによる別証明を,4次元概複素多様体Mの中の(必ずしも有向でない)連結閉曲面Fという状況に拡張したもので,主な道具は交差理論である. トポロジーの発展,殊に,代数的な道具立てが整備されるに伴い,その出自たる幾何学的「現場」に立ち帰ることは忘れられがちであるが,本論文及び3編の参考論文に現れた,出来るだけ「初等的」な考察によって幾何学的事態を明らかにするという論文提出者の立場は貴重なものと言わねばならない. 以上の理由により,論文提出者山田裕一氏は,博士(数理科学)の学位を受けるにふさわしい充分な資格があると認められる. |