この論文で、Wavelet理論におけるD.ColellaとC.Heilの予想を証明した。  はdilation方程式と呼ばれる。ここで、係数は、条件  を満たすと仮定する。この方程式のnonzero解はscaling functionと呼ばれる。もし、係数(cO,…,cN)がCohenの条件を満たせば、任意の一つのscaling函数から、一つのwaveletを作れる。このwaveletの連続性はscaling函数の連続性より決まる。最近のwavelet研究では、scaling函数の連続性についての研究は多い。1992年、I.Daubechiesは初めて、dilation方程式の研究で以下のようなdyadicの方法を採用した。 まず、方程式(1)をvector函数より書き直す。係数(cO,…,cN)に対して、もし連続で、compactな台を持つ解があれば、supp(f)⊂[0,N]だから、vector函数 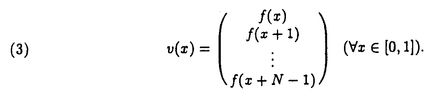 は函数f(x)の全部の情報を含んでいる。 二つのN×Nの行列を(T0)i,j=C2i-j-1,(T1)i,j=C2i-jと定義する。即ち、 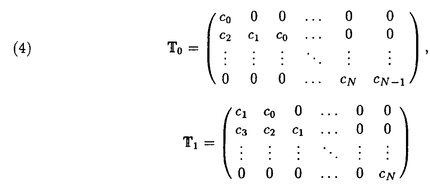 とするx∈[0,1]に対し 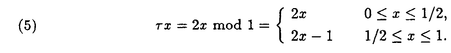 と定義すれば、dilation方程式は次の様なvector方程式になる 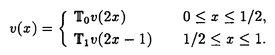 f(x)が連続とすれば、v(x)も連続で、逆もいえる。 この研究で、最初の問題は係数について、どんな条件を付けると,対応する函数f(x)が連続になるかという事である:この問題は1994年D.ColollaとC.Heilより完全に解決された。彼らの結論は曲面(2)の下で、函数f(x)が連続函数になる係数(cO,…,cN)の集合は、次の様に与えられる 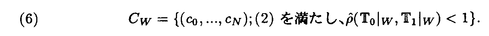 ここで 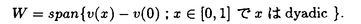 (2)式により、行列T0、T1の中で各列の成分を足すと全部1になるので、一般的に 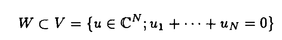 が成り立つ。1994年D.ColellaとC.Heilは次の予想をした: 予想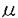 {(CO,…,CN)∈CW;W≠V}=0 in 曲面(2)。 {(CO,…,CN)∈CW;W≠V}=0 in 曲面(2)。 この論文で、次の事を証明した。 定理5.1(主定理)予想は正しい。 この定理の証明のため、まずcompact台のdistrbutionの整数移動に対する線形独立の概念を紹介する。f∈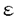 ’(R)とする。 ’(R)とする。 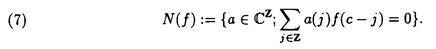 定義もしN(f)={0}ならば、fは整数移動について線形独立という。 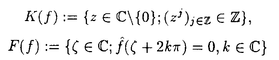 と記すと、Ronは1989年、次の事を証明した。 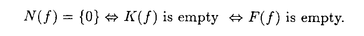 更に、 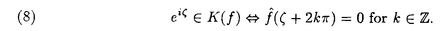 言い換えると、もし、fが線形従属であれば、∃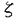 ∈C ∈C  この論文はまず次の命題を示す: 命題5.3f(x)は線形独立である⇒W=V。 命題5.3により 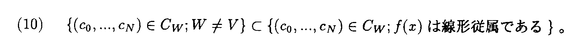 故り、主定理は次の命題に帰着した。 命題5.4 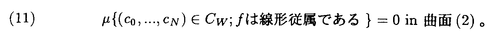 命題5.4の証明が本質的なので、以下命題5.4の証明の方針を述べる。 まず(11)の集合を、Sと記し、二つの集合 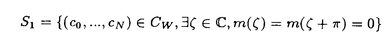 と 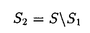 に分けて、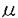 (S1)=0と (S1)=0と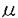 (S2)=0の証明ができれば、証明が終わる。 (S2)=0の証明ができれば、証明が終わる。 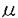 (S1)=0の証明は、S1を二つの集合の直積として、Fubiniの定理を使うと証明できる。予想の証明のpointは (S1)=0の証明は、S1を二つの集合の直積として、Fubiniの定理を使うと証明できる。予想の証明のpointは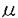 (S2)=0の証明である。 (S2)=0の証明である。 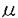 (S2)=0の証明において、まずfは線形従属なので、ある (S2)=0の証明において、まずfは線形従属なので、ある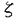 ∈Cに対し(9)が成り立つ。一方、ここでのfがcompact台のdistrbutionというだけでなく、scaling函数でもあるので、次の式も満たす ∈Cに対し(9)が成り立つ。一方、ここでのfがcompact台のdistrbutionというだけでなく、scaling函数でもあるので、次の式も満たす  但し、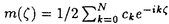 。論文は(9)と(12)の両方を出発点として、詳しい分析により、K(f)の構造は次のようである事が分かる: 。論文は(9)と(12)の両方を出発点として、詳しい分析により、K(f)の構造は次のようである事が分かる: K(f)はいくつかの次のような輪より得られる集合である: 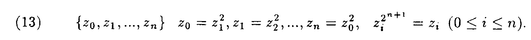 一方、この論文は次のことを証明する、 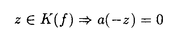 但し、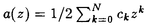 。故に 。故に 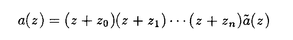 と書ける。 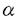 (z)の係数(cO,…,cN)より得た集合の自由度は( (z)の係数(cO,…,cN)より得た集合の自由度は(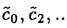 )できまるので、このような )できまるので、このような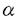 (z)の係数より得た集合は曲面(2)中の測度0の集合である。 (z)の係数より得た集合は曲面(2)中の測度0の集合である。 一方、Nを固定すると、(13)の様な数列は有限個しかないので、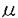 (S2)=0。これにより予想の証明は完全にできる。 (S2)=0。これにより予想の証明は完全にできる。 そのほか、論文はm(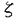 )を詳しく分析する。もし )を詳しく分析する。もし 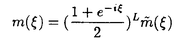 と書けると仮定しょう。但し、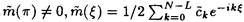 。よく知られているようにLが大きければ大きいほどf(x)は滑らかとなる。論文は更にm( 。よく知られているようにLが大きければ大きいほどf(x)は滑らかとなる。論文は更にm(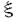 )の整数部分Imと小数部分Dmを次のように定義する: )の整数部分Imと小数部分Dmを次のように定義する: 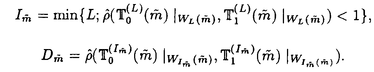 この定義の下で次のことが証明された: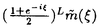 に対応する函数をf(x)とする。 に対応する函数をf(x)とする。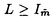 ならば ならば 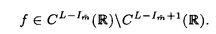 ここでCn(R)はn階連続微分可能の函数空間を表す。更に、参考論文で証明したように函数 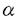 max(cO,…,cN)=sup{ max(cO,…,cN)=sup{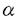 ;f(x)は ;f(x)は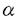 指数でHolder連続である} 指数でHolder連続である} の不連続点の集合は曲面(2)の中の測度0の集合である。 |