領域D⊂Rn上のC2関数fに対し、{(x,f(x))∈Rn+1|x∈D}が自然にRn+1上の曲面と定義され、fのグラフと呼ばれる。fが次の方程式 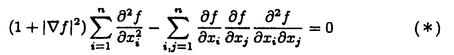 の解であるとき、fのグラフを極小グラフと呼ぶ。 1915年、Bernsteinは次のことを証明した(Bernsteinの定理): f:R2→Rが(*)の解であるとき、fは線形関数である、あるいはR3上の完備な極小グラフは平面しかない。60年代、Almgren,Simons等は次々にf:Rn→R(n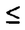 7)について同様のことを証明した。Bombieri,deGiogeとGiustiはn 7)について同様のことを証明した。Bombieri,deGiogeとGiustiはn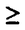 8の時自明でない解の存在を証明した。 8の時自明でない解の存在を証明した。 Bernsteinの定理の拡張は二つある。その1、Rn上の安定な極小超曲面の曲率の評価。(極小グラフはvolume minimizingで従って安定である)。その2、極小部分多様体の一意性の研究。例えば、Mはユークリッド空間の完備なn次元極小部分多様体のとき、加須栄は「Mが"無限遠で平坦"かつMが"一つのエンド"をもつなら、Mは平坦になる」を証明した。一方、Andersonは「Mが一つのエンドをもち、かつMがtotal scale curvature有限なら、Mはn次元アフィン平面になる」を証明した。 われわれは、極小部分多様体の体積関数を中心にして研究する。まずユークリッド空間Rm上の完備な極小部分多様体Mの体積関数Vol(M∩B(t))とMの無限遠での位相との関係を調べる。こごでB(t)はRm上の半径tの測地球で、無限遠での位相とはMのエンドの数(k(M)と書く)である。AはMの第二基本式、rはRmの距離関数とする。Mが無限遠で平坦とは 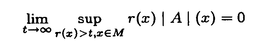 ということである。 主要結果: 定理一:MがRn上の完備の極小部分多様体とする。Mは"無限遠で平坦"或いは"∫M|A|n<∞"とする。n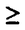 3或いはn=2かつMの任意のエンドが埋め込みとき 3或いはn=2かつMの任意のエンドが埋め込みとき 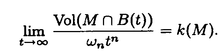 こごで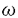 nはRnの単位球の体積である。 nはRnの単位球の体積である。 定理一は加須栄とAndersonの一意性定理の一般化である。更に、次の定理を証明した。 定理二:MかRn上の完備の極小部分多様体とする。 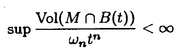 のとき、 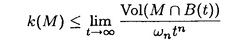 が成り立つ。 n=2の場合、次のことがわかった。 定理三:MがRn上の完備の極小曲面とする。このときMが全曲率有限の必要十分な条件は:ある定数cが存在して、 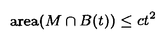 をみたし、かつMのgenusが有限である。 最後に、われわれは一般なリーマン多様体について、その極小部分多様体の体積増大度を評価する。仮定: N:完備なリーマン多様体で、断面曲率は上からcで押さえられる。 M:Nのはめ込まれたn次元完備極小部分多様体。 r:Nの一点pに関するの距離関数。 BN(t):Nの一点pに関する測地球。 ip:Nのp点での単射半径。 Fc(t):断面曲率cのn次元空間形の半径tの測地球の体積。 M(t):Mの半径tの測地球。 定理四:c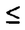 0のとき、関数 0のとき、関数 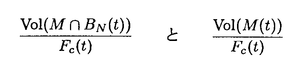 は(0,ip)の間で単調非減少である。 定理五:c>0のとき、関数 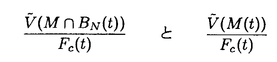 は(0,min(ip,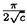 ))の間で単調非減少である。こごで、 ))の間で単調非減少である。こごで、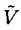 は、modified体積関数と呼ばれ、Mの領域Dに対して、次に定義する。 は、modified体積関数と呼ばれ、Mの領域Dに対して、次に定義する。 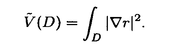 |