| 内容要旨 | | この論文の目的は二つある。ひとつはクレパントな特異点解消の構成、もうひとつは3次元版のMcKay対応の構成である。以下はそれぞれの要旨である。 (1)クレパントな特異点解消(crepant resolution)の構成 ここではSL(3,C)のある有限部分群による商特異点の特異点解消のうち、標準束を自明に保つものを構成し、その特異点解消によってできる極小モデルのオイラー数が、その群の共役類の数と一致することを示したい。 この問題は超弦理論から出てきたもので、Calabi-Yau多様体の研究とも深い関わりがある。超弦理論では多様体Mの有限群Gによる商空間M/Gの中での弦の伝播を考える。"オービフォールドのオイラー数"が 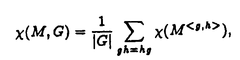 で定義される([DHVW])。ここで和は、Gの元の可換な組すべてでとり、M<g,h>はgとhの両方で固定される点全体の集合とする。 群GがMの標準束に自明に作用すると仮定するとき、次のような予想があった。 予想1.([DHVW]) 特異点解消 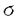 : :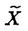 →M/Gで →M/Gで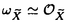 となるものが存在して、 となるものが存在して、 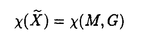 が成り立つ。 この物理学者たちによる等式(1985年)を、Hirzebruch、HoferがMがC2で群GがSL(2,C)のとき正しいことを示した。同時に3次元に対して特にM=C3でGがSL(3,C)の有限部分群の場合、次のような予想として発表した。(1990年) 予想2.([HH]) 群GがSL(3,C)の有限部分群とし、X=C3/Gを商特異点とする。このときXの標準束を自明に保つような特異点解消(crepant resolution)f: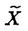 →Xが存在する。更に、 →Xが存在する。更に、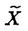 の位相的オイラー数が群Gの共役類の数と一致する。 の位相的オイラー数が群Gの共役類の数と一致する。 ちなみにcrepant resolutionは極小特異点解消になっており、この特異点解消が存在すると、上記のXの極小モデルが非特異であることがわかる。 この問題は、Markushevichら(1987年)とRoan(1989年)が、可換な群に対してトーリック幾何学で解決できることを示してから、何年も解けなかった。1992年になってMarkuchevichが、超曲面特異点の例について、具体的に定義方程式を用いてブローアップするという方法で証明した。続いて、1993年にRoanが、他の超曲面の例についても同様の方法が有効であることを示した。ここまででSL(3,C)の有限部分群のうち可換群と単純群についてはわかっていた。 そこで[I1,I2]では、群Gが対角行列と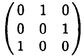 で生成されるような非可換群である場合を考えた。この群をtrihedral群と名付けた。この群によってできるXはトーリック多様体ではない。またXのほとんどは超曲面でもないので、それまでに知られていた方法は使えなかった。更にこの群の構造は、2次元のDn型特異点を決める群の3次元版とみなせるが、Xの特異点はDnの様に孤立特異点ではない。そこで、トーリック特異点解消から得られる幾何学的な情報と、群Gの可解性をうまく用いた新しい特異点解消の方法を見いだした。 で生成されるような非可換群である場合を考えた。この群をtrihedral群と名付けた。この群によってできるXはトーリック多様体ではない。またXのほとんどは超曲面でもないので、それまでに知られていた方法は使えなかった。更にこの群の構造は、2次元のDn型特異点を決める群の3次元版とみなせるが、Xの特異点はDnの様に孤立特異点ではない。そこで、トーリック特異点解消から得られる幾何学的な情報と、群Gの可解性をうまく用いた新しい特異点解消の方法を見いだした。 第2章では、群Gの不変式が単項的であるような群に対して、クレパントな特異点解消を構成している。これは先のtrihedralの場合をも含んでいる。その特異点解消は以下のような図式を満たすものである。 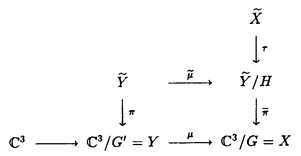 この中で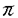 はYの特異点解消であり、 はYの特異点解消であり、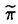 はそれから導かれる写像であり、rはH はそれから導かれる写像であり、rはH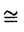 G/G’による特異点の解消である。そして G/G’による特異点の解消である。そして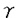 o o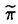 がXのcrepant resolutionになっている。 がXのcrepant resolutionになっている。 つまり、trihedral群の場合に用いた特異点解消の方法が、もっと一般のmonomial群に対して拡張できることを示している。 なお、上の予想2に関してはRoan(1994年[R])が最終的にSL(3,C)のすべての有限部分群に対してHirzebruch、Hoferの予想が正しいことを証明した。そこで用いられた手法はすでに上で構成された特異点解消の方法であり、残りの他の群に対しても有効であることが示されたことになる。これらについては第3章で述べる。 (2)3次元McKay対応 SL(3,C)の場合のHirzebruch、Hoferの予想の解決によって、特異点解消のオイラー数が共役類の数と一致することがわかった。しかしこれによってわかるのは、オイラー数と共役類の数値的な一致である。そこで更にその一致の数学的根拠を調べたものが、この部分の主結果である。 SL(2,C)の場合、McKay対応と呼ばれる特異点と群の表現等のさまざまな対応が知られている。それによってこの数字の一致も説明できる。 これはもともとReid氏の予想であったが、著者の結果である(1)のmonomial群による特異点の解消の構成過程で得られた幾何学的情報と、2次元の場合の著者の例(本論文の3章参照)がもとになっている。この3次元のMcKay対応では、2次元のMcKay対応と異なり、特異点解消のオイラー数に関する等式が、特異点解消の例外因子と共役類の対応として説明される。 群GをSL(n,C)の有限部分群であるとし、X=Cn/Gとする。Crepant divisorは任意の特異点解消に例外因子として現れる。この論文ではcrepant divisorがage1の共役類と1対1対応を持つことを示した。 この応用として、SL(3,C)の場合極小特異点解消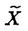 のベッチ数がその次数の のベッチ数がその次数の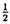 倍のageの共役類と対応しており、その交代和つまりオイラー数が、ちょうどすべての共役類と対応していることがわかる。 倍のageの共役類と対応しており、その交代和つまりオイラー数が、ちょうどすべての共役類と対応していることがわかる。 (1)はコホモロジー群の次元の交代和と群の共役類の数の一致のみであったが、(2)は例外因子とコホモロジー群との直接の対応をつけたという意味で、より深い結果である。 この部分の主な結果は 定理2.1.群GをSL(n,C)の有限部分群とし、その商特異点X=Cn/Gの特異点解消をX’とする。このときX’の中のクレパントな例外因子と群Gの共役類のうちageが1のものとが1対1対応している。 というものである。ageというのはGのすべての元gに対して定義できるもので、gの固有値の指数の和である。なおXがn次元のとき、群GがSL(n,C)の有限部分群であることよりageは0以上n-1以下の整数である。 Xがクレパントな特異点解消Xを持つ場合は次のようになる。 系2.2.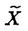 の例外因子はすべて群Gのage1の共役類と1対1対応している。 の例外因子はすべて群Gのage1の共役類と1対1対応している。 3次元の場合は、定理0よりクレパントな特異点解消が存在することがわかっているのでオイラー数に関する更に深い結果として次を得た。 定理2.3.群GがSL(3,C)の有限部分群であり、X=C3/Gのクレパントな特異点解消をf: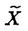 →Xとする。このとき各ベッチ数と共役類は次のように対応している。 →Xとする。このとき各ベッチ数と共役類は次のように対応している。 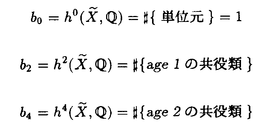 また更にage1の共役類はすべての例外因子と、age2の共役類はXの原点上のファイバーf-1(0)の中にある例外因子と1対1対応している。 定理2.1の証明において、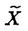 のクレパントな例外因子を考えるかわりにXのクレパントな離散付値で考えた。この離散付値の分岐理論を用いると、例外因子のdiscrepancyの計算が標数が0ということから巡回群の場合に帰着できる。そして巡回群の場合はトーリック多様体になるので、トーリック幾何学の手法を使って確かめることができた。 のクレパントな例外因子を考えるかわりにXのクレパントな離散付値で考えた。この離散付値の分岐理論を用いると、例外因子のdiscrepancyの計算が標数が0ということから巡回群の場合に帰着できる。そして巡回群の場合はトーリック多様体になるので、トーリック幾何学の手法を使って確かめることができた。 ここに現れる特異点は、超曲面でも完全交叉でもないものがたくさんあり、多くは孤立特異点でもない。また群Gが非可換な場合はトーリック多様体でもない。しかしtrihedral特異点のクレパントな特異点解消を構成したときと同様に、トーリック幾何学が有効であった。また群Gが非可換でXが複雑になる場合でも、すべて証明は群Gが巡回群である場合に帰着できるということもわかった。 また更に2次元の場合、系2.2の応用として極小特異点解消はクレパントであり、ageは単位元以外はすべて1であることから例外因子と共役類の1対1対応がいえる。こうしてSL(2,C)の場合、従来の特異点と群の表現のMcKay対応だけでなく、特異点と共役類の対応として、特異点解消の例外因子の構造も含めて説明できることになった。しかも表現を用いたときと同様に、Dynkin図形が構成できることもわかる。 謝辞 この博士論文制作に際しての川又雄二郎先生のご指導、ご助言に心より感謝いたします。1995年秋イギリスのWarwick大学にて、研究内容についての発表や多くの方と議論する機会を与えてくださったMiles Reid先生にも感謝いたします。 また著者の研究、海外渡航の援助をしてくださった風樹会、数理科学振興会、学術振興会のみなさまにも心より御礼申し上げます。 REFERENCES[BM] J.Bertin and D.Markushevich,Singularites quotients non abeliennes de dimension 3 et varietes de Calabi-Yau,Math.Ann.299(1994),105-116.[DHVW]L.Dixon,J.Harvey,C.Vafa and E.Witten,Strings on orbifolds(I),Nucl.Phys.B261(1985),678-686.[DHVW]_,Strings on orbifolds(II),Nucl.Phys.B274(1986),285-314.[HH] F.Hirzebruch and T.Hofer,On the Euler number of an orbifold,Math.Ann.286(1990),255-260.[I1] Y.Ito,Crepant resolution of trihedral singularities,Proc.Japan Acad.Ser A 70 No.5(1994),131-136.[I2] _,Crepant resolution of trihedral singularities and the orbifold Euler characteristic,to appear in Intern.Jour.of Math..[Mc] McKay,Graphs,singularities,and finite group,in Santa Cruz,conference on finite groups(Santa Cruz,1979),Proc.Symp.Pure Math.,AMS 37(1980),183-186.[Ma] D.Markushevich,Resolution of C3/H168,preprint(1992).[MOP] D.G.Markushevich,M.A.Olshanetsky and A.M.Perelomov,Description of a class of superstring compactifications related to semi-simple Lie algebras,Comm.Math.Phys.111(1987),247-274.[R1] S.-S.Roan,On the generalization of Kummer surfaces,J.Diff.Geometry 30(1989),523-537.[R2] _,On c1=0 resolution of quotient singularity,Intern.Jour.of Math.5(1994),523-536.[R3] _,Minimal resolutions of Gorenstein orbifolds in dimension three,Preprint R940606-1,Acad.Sinica,Taibei,Jun 1994. |
| 審査要旨 | | 論文提出者 伊藤 由佳理 は、SL(3、C)の有限部分群による商特異点を研究し、いくつかのめざましい結果を得た。この論文の前半ではクレパントな特異点解消の存在とオイラー数に関する等式を証明し、後半ではそれを更に進めて3次元版のMcKay対応を構成している。 この問題は超弦理論から出てきたもので、Calabi-Yau多様体の研究とも深い関わりがある。いわゆるオービフォールドオイラー数に関する物理学者たちによる等式(1985年)をもとにして、HirzebruchとHoferが次のような予想を発表した。(1990年):群GがSL(3,C)の有限部分群とし、Xを商特異点とする。このときXの標準束を自明に保つような特異点解消(crepant resolution)X’が存在する。更に、その位相的オイラー数が群Gの共役類の数と一致する。ちなみにcrepant resolutionは極小特異点解消になっており、この特異点解消が存在すると、上記のXの極小モデルが非特異であることがわかる。この問題は、Markushevichら(1987年)とRoan(1989年)が、可換な群に対してトーリック幾何学で解決できることを示し、1992年になってMarkuchevichが、超曲面特異点の例について、具体的に定義方程式を用いてブローアップするという方法で証明した。続いて、1993年にRoanが、他の超曲面の例についても同様の方法が有効であることを示した。そこで伊藤氏は、群Gが対角行列と位数3の元で生成されるような非可換群である場合を考え、この群をtrihedral群と名付け、この場合に予想を解決した。さらに伊藤氏は、より一般に群Gの不変式が単項的であるような場合に、クレパントな特異点解消を構成し、予想を確認した。これは先のtrihedralの場合を含んでいる。なお、上の予想に関してはRoan(1994年)が最終的に残りの場合も証明した。 オイラー数の式の奥に潜む幾何学的根拠を調べたものが、後半部分の主結果である。SL(2,C)の場合には、McKay対応と呼ばれる特異点と群の表現等の間の対応が知られている。これを3次元に拡張するのである。この3次元のMcKay対応では、2次元のMcKay対応と異なり、特異点解消のオイラー数に関する等式が、特異点解消の例外因子と共役類の対応として説明される。この部分の主要結果は:X’の中のクレパントな例外因子と群Gの共役類のうちageが1のものとが1対1対応している。ここで、ageというのはGの元gに対して定義できるもので、gの固有値の指数の和である。 よって、論文提出者 伊藤 由佳理 は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 |