本論文では、数理物理に現れるシュレディンガー方程式と波動方程式の連立方程式系の孤立波解の安定性について考察する。非線形シュレディンガー方程式や非線形波動方程式など単独の非線形保存系偏微分方程式の孤立波解の安定性及び不安定性に関しては’80年代初頭より多くの研究者によって研究されてきた。特に、単独の非線形シュレディンガー方程式の孤立波解の安定性・不安定性に関する数学的研究は、主に変分法を用いてBerestycki and Cazenave(’81),Cazenave and Lions(’82),Weinstein(’83)などにより始められた。また、単独の非線形クライン・ゴルドン方程式の孤立波解の安定性・不安定性に関しては、Shatah(’83),Shatah and Strauss(’85)などにより研究された。その後、非線形シュレディンガー方程式、非線形クライン・ゴルドン方程式、一般化されたKdV方程式などの孤立波解の安定性・不安定性の問題はGrillakis,Shatah and Strauss(’87,’90)により線形化作用素のスペクトル解析を用いて抽象的な枠組にまとめられた。しかし、それらが連立した方程式系に関しては初期値問題の可解性については詳しく研究されているが、孤立波解の安定性については、これまであまり研究されていないように思われる。 本論文では、第0章で歴史的背景などを述べた後、第1章では光ファイバー中のパルスの伝播を記述するモデルなどに現れる3次の非線形項をもつ空間1次元の非線形シュレディンガー方程式系を、第II章では湯川相互作用をもつ空間3次元のクライン・ゴルドン・シュレディンガー方程式系を、第III章ではプラズマ物理に現れるシュレディンガー方程式と波動方程式の連立した空間1次元のザハロフ方程式系を取り上げ、それらの孤立波解の安定性を示す。いずれも数理物理に現れる連立非線形偏微分方程式系であり、それらの孤立波解の安定性を調べることは数学的にも物理的にも興味深いことであるが、これまでは少なくとも数学的に厳密な結果はあまり得られていなかった。本論文では、主に単独の非線形シュレディンガー方程式の基底定常解から生成される孤立波解の安定性を示したCazenave and Lions(’82)による変分法を用いる方法を自然に拡張し、それぞれの連立方程式系の孤立波解の安定性を示す。なお、本論文で扱う連立方程式系の孤立波解は、いずれも対応する単独方程式の孤立波解から作られるが、たとえ単独方程式の解として安定であっても、連立方程式系の解構造はより複雑であるから、一般に連立方程式系の孤立波解の安定性は、対応する単独方程式の孤立波解の安定性から直ちには導かれないことに注意する。実際、単独方程式の安定孤立波解から作られる連立方程式系の孤立波解で、その安定性が不明であるような例は多く存在する。 以下、各章における主結果を述べる。第I章では、単独の3次の非線形項をもつ空間1次元の非線形シュレディンガー方程式: 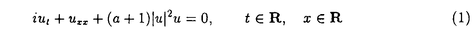 の自然な拡張と考えられる次の連立系を取り上げる。ここで、a>-1は定数である。  ここで、(2)はuと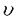 に関して対称だから(1)の孤立波解u(t,x)=eiwt に関して対称だから(1)の孤立波解u(t,x)=eiwt w(x)から(2)の孤立波解(u(t), w(x)から(2)の孤立波解(u(t),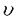 (t))=(eiwt (t))=(eiwt w,eiwt w,eiwt w)が得られる。ここで、w>0で w)が得られる。ここで、w>0で wは wは 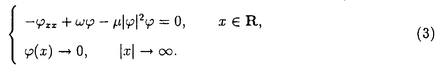 の =a+1のときの解である。このとき、任意のw>0に対して(1)の孤立波解u(t)=eiwt =a+1のときの解である。このとき、任意のw>0に対して(1)の孤立波解u(t)=eiwt wが安定であることはCazenave and Lions(’82)により示されている。第I章では次の結果を示す。 wが安定であることはCazenave and Lions(’82)により示されている。第I章では次の結果を示す。 定理I.a>-1とする。任意のw>0に対して(2)の孤立波解(u(t), (t))=(eiwt (t))=(eiwt w,eiwt w,eiwt w)は安定である。 w)は安定である。 定理Iの証明は、単独の定常問題(3)の解 wから作られる( wから作られる( w, w, w)が、連立方程式系(2)に対応する定常問題の基底状態解であることを示すことによりなされる。なお、a>0のときは w)が、連立方程式系(2)に対応する定常問題の基底状態解であることを示すことによりなされる。なお、a>0のときは wを wを =aのときの(3)の解とすると、(2)の孤立波解(u(t), =aのときの(3)の解とすると、(2)の孤立波解(u(t),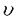 (t))=(eiwt (t))=(eiwt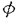 w,0)(0,eiwt w,0)(0,eiwt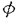 w)が安定であることも同様にして示すことができる。 w)が安定であることも同様にして示すことができる。 第II章では湯川相互作用をもつクライン・ゴルドン・シュレディンガー方程式系: 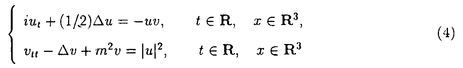 を考える。ここで、uは複素数値、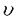 は実数値関数で、mは実定数。(4)の孤立波解(u(t,x), は実数値関数で、mは実定数。(4)の孤立波解(u(t,x),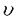 (t,x))=(eiwt (t,x))=(eiwt w(x), w(x), w(x))の安定性を考える。ここで、w>0で( w(x))の安定性を考える。ここで、w>0で( w, w, w)は w)は 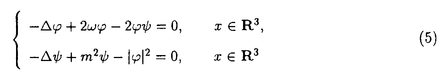 の基底状態解とする。ここでは簡単のためm=0の場合だけ考える。このとき、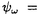 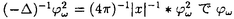 は は 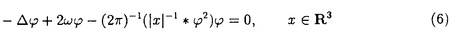 の正値球対称解である。 定理II.m=0とする。任意のw>0に対して(4)の孤立波解(u(t),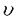 (t))=(eiwt (t))=(eiwt w(x) w(x) w(x))は安定である。 w(x))は安定である。 上で定義されたu(t,x)=eiwt w(x)は単独の非線形シュレディンガー方程式: w(x)は単独の非線形シュレディンガー方程式: 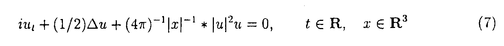 の孤立波解であるが,それが安定であることは、Cazenave and Lions(’82)により示されている。一方、単独の非線形クライン・ゴルドン方程式の時間に依らない基底定常解はすべて不安定であることが、Berestycki and Cazenave(’81)とShatah(’85)によって示されている。第II章では、m>0の場合も含めて(u(t,x),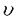 (t,x))=(eiwt (t,x))=(eiwt w(x), w(x), w(x))という形のクライン・ゴルドン方程式とシュレディンガー方程式の連立系(4)の安定な孤立波解が存在することを示す。 w(x))という形のクライン・ゴルドン方程式とシュレディンガー方程式の連立系(4)の安定な孤立波解が存在することを示す。 第III章では、プラズマ物理に現れるシュレディンガー方程式と波動方程式の連立した空間1次元のザハロフ方程式系: 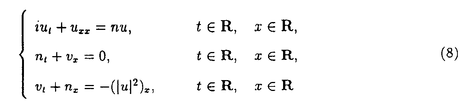 を考える。ここで、uは複素数値、nと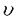 は実数値関数。(8)の孤立波解(u(t,x),n(t,x), は実数値関数。(8)の孤立波解(u(t,x),n(t,x),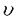 (t,x))=(expi[(c/2)x-(c2/4)t+wt] (t,x))=(expi[(c/2)x-(c2/4)t+wt] w,c(x-ct), w,c(x-ct), w,c(x-ct),c w,c(x-ct),c w,c(x-ct))の安定性を考える。ここで、 w,c(x-ct))の安定性を考える。ここで、 で で w,cは w,cは =(1-c2)-1のときの(3)の解である。 =(1-c2)-1のときの(3)の解である。 定理III.任意のw>0,-1<c<1に対して(8)の孤立波解(u(t,x),n(t,x), (t,x))=(expi[(c/2)x-(c2/4)t+wt] (t,x))=(expi[(c/2)x-(c2/4)t+wt] w,c(x-ct),(eiwt w,c(x-ct),(eiwt w,c(x), w,c(x), w(x))は安定である。 w(x))は安定である。 定理IIIの証明は、ザハロフ方程式系(8)のエネルギーと対比する単独の非線形シュレディンガー方程式:  のエネルギーとの関係を導き、単独方程式(9)の孤立波解  が安定であることを利用してなされる。なお、定理IIIと類似の結果がWu(’94)とLaurencot(’95)によって別の証明方法を用いて独立に発表されている。 |