我々は部分多様体同士の交叉について、もっと研究しなければならない。 なぜならば、たとえば、"高次元linkのlink cobordismによる分類"という,多様体やその埋め込みを考える上で基礎的な問題が未解決である。高次元knotのcobordismによる分類はSeifert hypersurfaceのsurgeryが、うまくできるので,すでになされている。linkの場合は、linkの各成分にSeifert hypersurface(という部分多様体)を張ったとき一般にはお互いが交叉するため困難がある。(高次元knot(link)cobordismについては,本編のReferenceを参照せよ。) 本稿では、部分多様体同士の交叉についての新理論を構築するために次の観点を提出する。『部分多様体同士の交叉は、もとのそれぞれの部分多様体の中で新たな部分多様体になっている。その埋め込みのタイプに注目する。』この観点からPart I-IVのような問題を提出して疑問に答える。これらの問題は、高次元knotの新型問題でもある。 PartI 5次元球面S5の中で、2つの3次元球面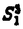 、 、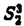 が、それぞれ埋めこまれていてお互いにtransverseに交わっているとする。これを が、それぞれ埋めこまれていてお互いにtransverseに交わっているとする。これを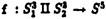 と書く。ここにf( と書く。ここにf(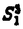 )∩f( )∩f(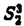 ) in ) in 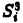 (i=1,2)という2つの1次元絡み目が得られた。またf( (i=1,2)という2つの1次元絡み目が得られた。またf(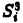 ) in S5(i=1,2)という2つの3次元結び目が得られた。ここで『2つの1次元絡み目L1,L2、と2つの3次元結び目X1,X2が与えられた時、上のようなあるfがあって上のような4組として実現されるための条件を求めよ。』という問題を考える。 ) in S5(i=1,2)という2つの3次元結び目が得られた。ここで『2つの1次元絡み目L1,L2、と2つの3次元結び目X1,X2が与えられた時、上のようなあるfがあって上のような4組として実現されるための条件を求めよ。』という問題を考える。 次のようにArf invariant と mod2 linking numberで特徴付けられる。 『定理.次の(1)と(2)は同値である。 (1)2つの1次元絡み目L1=(K11,…,K1m),L2=(K21,…,K2m),と2つの3次元結び目X1,X2が与えられた時、上のような4組として実現される。 (2)2つの1次元絡み目L1,L2,と2つの3次元結び目X1,X2がつぎの(i)、(ii)のうちいずれかを満たす。 (i)L1とL2がともにproper linkであって Arf(L1)=Arf(L2) (ii)L1とL2がともにnon proper linkであって lk(K1j,L1-K1j)≡lk(K2j,L2-K2j) mod 2 for all j』 必要性の示し方。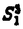 のSeifert surfaceをViとする。V1∩V2がK1、K2それぞれのSeifert surfaceのrel ∂なframed cobordismを与えることに注目する。Arf invariantとmod2 linking numberを のSeifert surfaceをViとする。V1∩V2がK1、K2それぞれのSeifert surfaceのrel ∂なframed cobordismを与えることに注目する。Arf invariantとmod2 linking numberを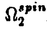 を使ってよみかえて、 を使ってよみかえて、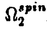 に障害があることを示す。十分性は、後述。 に障害があることを示す。十分性は、後述。 さらに次のことも調べた。self-transeverese immersion f:S3→S5でsingular point set C in S5がconnectedなものを考える。するとf-1(C)in S3は2成分1次元linkか1次元knotになる。ここで『上のf-1(C)in S3として、どのようなものが得られるか?』という問題を考える。答えは、次のようになる。 『定理.すべての2成分1次元linkおよび1次元knotが得られる。』 ここで次の事実が興味を魅く。最初の方の結果では、f(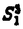 )∩f( )∩f(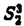 ) in f( ) in f(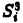 )がi=1の方は自明なknot、i=2の方はtrefoil knotということはいかなるfに対しても起こり得ない。しかし後の方の結果では、適当なfに対してf-1(C)in S3が、2成分split linkであってその成分が、一方が自明なknot、他方がtrefoil knotというものになる。 )がi=1の方は自明なknot、i=2の方はtrefoil knotということはいかなるfに対しても起こり得ない。しかし後の方の結果では、適当なfに対してf-1(C)in S3が、2成分split linkであってその成分が、一方が自明なknot、他方がtrefoil knotというものになる。 PartII (n+4)-次元球面Sn+4の中で、2つの(n+2)-次元球面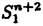 、 、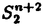 が、それぞれ埋めこまれていてお互いにtransverseに交わっているとする。これを が、それぞれ埋めこまれていてお互いにtransverseに交わっているとする。これを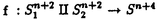 と書く。ここにf( と書く。ここにf(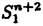 )∩f( )∩f(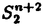 )in Sn+4という2つのn次元結び目が得られた。ここで『2つのn次元結び目K1,K2が与えられた時、上のようなあるfがあって上のようなpairとして実現されるための条件を求めよ。』という問題を考える。 )in Sn+4という2つのn次元結び目が得られた。ここで『2つのn次元結び目K1,K2が与えられた時、上のようなあるfがあって上のようなpairとして実現されるための条件を求めよ。』という問題を考える。 『定理.次の2つは同値である。 (1)2つのn次元knot K1,K2が上のようなpairとして実現される。 (2)2つのn次元knot K1,K2が次の条件を満たす。  knot cobordism theoryやsurgery theoryに現れるものと似た、次元に関するmod4周期があることに注意されたい。 必要性の示し方。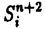 のSeifert surfaceをViとする。V1∩V2がK1、K2それぞれのSeifert surfaceのrel ∂なframed cobordismを与えることに注目する。Novikov additivityとframed manifoldの交叉積の性質を使う。十分性は、後述。 のSeifert surfaceをViとする。V1∩V2がK1、K2それぞれのSeifert surfaceのrel ∂なframed cobordismを与えることに注目する。Novikov additivityとframed manifoldの交叉積の性質を使う。十分性は、後述。 さらに次の結果も得た。先程のimmersion 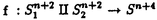 に関して、2つのn次元結び目f( に関して、2つのn次元結び目f(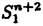 )∩f( )∩f(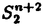 ) in Sn+4が得られることは前に見た。このときf( ) in Sn+4が得られることは前に見た。このときf(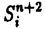 )in Sn+4(i=1,2)という2つの(n+2)-次元結び目も得られる。このとき次が成立する。 )in Sn+4(i=1,2)という2つの(n+2)-次元結び目も得られる。このとき次が成立する。 『定理.nを偶数とする。任意のn次元knots K1,K2と任意の(n+2)-次元knots X1,X2からなる4組(K1,K2,X1,X2)は、上のようなあるfに対して、上のような交叉によって実現される。』 証明法はZeemanの1-twist spun knotは自明になるという定理とKervaireの2n-knotはsliceであるという定理を使う。 PartIII 3個の4-sphere 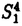 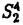 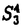 がS6にそれぞれ埋め込まれていて,お互いに交叉しているとする。 がS6にそれぞれ埋め込まれていて,お互いに交叉しているとする。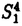 ∩ ∩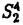 ∩ ∩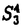 = =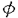 。 。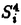 ∩ ∩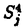 はconnectedとする。すなはちconnected oriented surfaceである。(n-次元でも同様に論じられる。)surfaceによる2-dimensional link Li=( はconnectedとする。すなはちconnected oriented surfaceである。(n-次元でも同様に論じられる。)surfaceによる2-dimensional link Li=(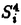 ∩ ∩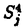 , ,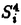 ∩ ∩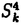 )が得られた。ただし(i,j,k)=(1,2,3),(2,1,3),(3,1,2)。このような(L1,L2,L3)としてどのようなものが得られるかを研究した。 )が得られた。ただし(i,j,k)=(1,2,3),(2,1,3),(3,1,2)。このような(L1,L2,L3)としてどのようなものが得られるかを研究した。 『定理.(L1,L2,L3)が上のような交叉として得られるとする。かつ、各Liはsemi-boundary linkとする。このとき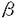 (L1)+ (L1)+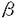 (L2)+ (L2)+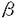 (L3)=0。ただし (L3)=0。ただし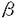 (Li)はLiのSato-Levine invariantである。』 (Li)はLiのSato-Levine invariantである。』 証明法について。Sato-Levine invariantは本来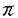 4S2に値をとるがこれを 4S2に値をとるがこれを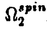 に値をとると見られることを示し、 に値をとると見られることを示し、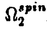 に障害を見い出す。 に障害を見い出す。 さらに上の定理とSato,Rubermenの結果より 『定理.ある(L1,L2,L3)は、上のような交叉として得られない。』 また次のことも示した。 『定理.もし各Liがsplit linkならば(L1,L2,L3)が上のような交叉として得られる。』 『定理.各Liがnon-semi-boundaryな、(resp.non-boundaryかつsemi-boundaryな、)ある(L1,L2,L3)が上のような交叉として得られる。』 また次のことを指摘した。 『各Liのcomponentがsphereとする。もしも(L1,L2,L3)で上のような交叉として得られないものがあれば次の有名な未解決問題に対する答がNoとなる。"すべての2-dimensional linkはsliceか?"』 PartIV PartIIの交叉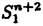 ∩ ∩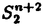 が、あるn次元PL connected closed oriented manifold Mとdiffeomorphicとする。 が、あるn次元PL connected closed oriented manifold Mとdiffeomorphicとする。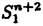 ∩ ∩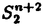 in in 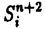 はn次元M-knots Kiを定義するとする。 はn次元M-knots Kiを定義するとする。 『定理.n=4m+3のとき。(K1,K2)が前述のような交叉として実現されるならば、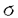 (K1)= (K1)=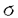 (K2)となる。』 (K2)となる。』 『定理.n=4m+1のとき。あるMに対して、かってなM-knotsのpair(K1,K2)が前述のような交叉として実現される。』 この定理はMのinertia群が自明でないことを系として含む。この系はBrown and Steerの結果を含む。 『定理.n=4m+1のとき。あるM1、M2に対してMi-knotsのPair(K1,K2)が前述のような交叉として実現されることは同値関係である。同値類はM1のとき2個。M2のとき3個。』 また次も示した。 『定理.nがevenのとき。あるMに対してM-knotsのあるpair(K1,K2)が前述のような交叉として実現されない。』(これらのK1,K2はcobordantでもない。) 『定理.n=4m+1(resp.n=4m+3)のとき。あるMに対して次のようなM-knotsのあるpair(K1,K2)が前述のような交叉として実現されない。M-knotsには、Arfinvariant(resp.signature)が定義されてArfK1=ArfK2(resp.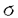 K1= K1=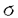 K2)。』(このような(K1,K2)にはSeifert行列がmatrix cobordantだがcobordantでないものもある。) K2)。』(このような(K1,K2)にはSeifert行列がmatrix cobordantだがcobordantでないものもある。) 一般のn次元manifoldMの埋め込みについて。MxD2への埋め込みはCappell and Shaneson等の高度な研究がある。Sn+2への埋め込みはさらに難しく、まだ研究すべきことは多い。上述のものは、ひとつのアプローチである。 共通する証明のアイデア。および今後の展望。 例えば、PartI前半では目的の絡み目を得るために、S5の中で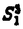 と と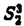 とを’submanifoldのsurgery’を使って下記のように変更していく。 とを’submanifoldのsurgery’を使って下記のように変更していく。 従来’submanifoldのsurgery’は、knot cobordism(Kervaire、Levine等)、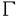 -theory(Cappell and Shaneson等)、link cobordism(Cochran and Orr等)、splitting theorem(Cappell、Browder等)等、いずれもsubmanifoldのdiffeomorphism typeをいかに簡単にするかという視点だった。しかし本稿では、次の通り。 -theory(Cappell and Shaneson等)、link cobordism(Cochran and Orr等)、splitting theorem(Cappell、Browder等)等、いずれもsubmanifoldのdiffeomorphism typeをいかに簡単にするかという視点だった。しかし本稿では、次の通り。 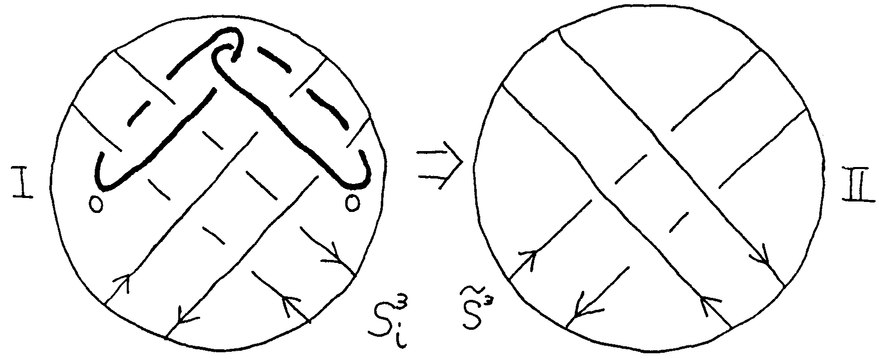 図表 図表 PartIでは。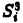 の中に上図Iの3-ballを取る。細線が の中に上図Iの3-ballを取る。細線が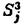 との交わり。(i≠j) との交わり。(i≠j)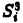 に4次元2-handle h2を太線で0-surgeryが施されるように、absoluteにattachする。 に4次元2-handle h2を太線で0-surgeryが施されるように、absoluteにattachする。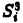 は再び3-sphere は再び3-sphere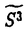 になる。 になる。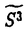 の中で細線の部分は、 の中で細線の部分は、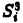 での細線の部分にpass-moveを施したものになる。(上図II。)実はh2を での細線の部分にpass-moveを施したものになる。(上図II。)実はh2を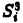 にattachするとき、h2をS5の中で{ にattachするとき、h2をS5の中で{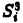 -attach part}とも -attach part}とも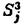 とも交わらずにattachできることを示す。この操作を繰り返して目的の絡み目を得る。すなはち、本稿では交叉による絡み目をいかに複雑にしていくかという視点である。 とも交わらずにattachできることを示す。この操作を繰り返して目的の絡み目を得る。すなはち、本稿では交叉による絡み目をいかに複雑にしていくかという視点である。 PartII、PartIV、では高次元pass-moveというものを新たに定義し、それといくつかの操作をsubmanifoldのsurgeryによって行い、交叉によるknotを複雑にしていく。 本稿では、submanifoldのsurgeryの拡張として交叉のある場合を扱った。これは、例えばpseudomanifold、intersection homology(Goresky and MacPhersonやCappell and Shaneson等の研究しているもの。)等と、関連して新分野となろう。 |