| 内容要旨 | | この論文では,河東,Evans,XuらによってAFDで行われていた,A2m+1型(quantum SU(2)2m型)subfactorや,さらに一般のquantum SU(n)k subfactorに対するorbifold constructionがAFDでない場合にも行えることを示す.この結果はPopaやRadulescuらによって構成されているnon-AFD SU(n)k subfactorなど,多くの例に適用することができる.また,orbifold constructionに現れるautomorphismが河東によって導入されたrelative Connes invariant X(M,N)と深く関わっていることから,AFDでない場合に,より代数的な不変量algebraic relative Connes invariant 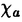 (M,N)を導入し,これがつねに可換群になることを示した.この (M,N)を導入し,これがつねに可換群になることを示した.この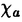 (M,N)を用いて最も一般的な状況におけるorbifold constructionについても議論する. (M,N)を用いて最も一般的な状況におけるorbifold constructionについても議論する. 1983年にV.F.R.Jonesがsubfactorにindexを導入してから,AFD(ap-proximately finite dimensional)II1 subfactorの分類が注目を浴びたが,これに対して,1987年にA.Ocneanuはindex<4のsubfactorの完全分類に関して以下のような主張をした,すなわち,index<4のAFD II1 subfactorは,Dynkin図形のAmとD2mのそれぞれに対して同型類が1つずつ,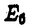 と と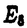 のそれぞれに対して,互いに反同型だが,同型でない2つの同型類が存在し,これがindex<4のAFD II1 subfactorの全てである. のそれぞれに対して,互いに反同型だが,同型でない2つの同型類が存在し,これがindex<4のAFD II1 subfactorの全てである. 彼は,この分類のために,paragroupという新たな概念を導入した.Subfactorの完全分類には,S.Popaのgenerating theoremという深い結果を使わねばならず,それにはAFDという仮定が欠かせない.しかし,Ocneanuによるparagroup理論は,subfactorの代数的かつcombinatorialな側面を扱っているために,完全分類には必要だったAFDという仮定は必要としない.Paragroup理論の展開の道具としては,type II1 subfactorの場合には,bimodule(両側加群),type II∞またはtype IIIのsubfactorの場合には,R.Longoによるsector理論が用いられている. 最近,共形場理論におけるorbifold constructionの方法が,可解格子模型に応用されているが,これに対し,この方法を初めてsubfactor理論に応用したのは河東である.彼は,Ocneanuの分類リストの一部であるprincipal graph D2mのsubfactorの存在と,principal graph D2m+1のsubfactorの非存在を証明するために,subfactor理論にorbifold constructionを導入したのであった.更に,D.E.Evansと河東は,orbifold constructionをSU(n)k型可解格子模型からくるsubfactor(これはsubfactor理論では既に知られていたH.WenzlのHecke algebra subfactorにあたる)の場合に拡張した.その後,F.Xuはこの方法を,flatnessに対するobstructionと共形場理論におけるconformal dimensionとの関係を明らかにすることによって,Wess-Zumino-Witten modelから生じるsubfactorの場合に適用する事に成功している.彼らの方法は,有限次元のcommuting squareに関する議論を使っているため,ここに現れたsubfactorは全てAFD II1であり,これをそのままAFDでない場合に拡張することはできなかった.しかし,orbifold constructionは,paragroupがある種の対称性を持っている時に,その対称性で"割る"という,代数的/combinatorialな方法であるので,これはAFDという仮定は必要としないはずである.AFDでなくてもできるだろう,という予想はされていたが,これまではテクニカルな困難のために,この予想は解かれていなかった.この論文では,bimoduleのテクニックを用いることによって,AFDでない場合にも,AFDの時と同様にorbifold constructionが行えることを示す. 第1章は,以下の章の準備のために,記号や基本的な概念の定義,その性質などを与えた. 第2章では,factorのtypeによらずに,principal graph D2mのsubfactorがprin-cipal graph A4m-3のsubfactorから,その上のnon-strongly outer automorphismによるZ2-同時接合積をとることによって,構成できることを示す.この結果は,Popaのnon-AFD type II1のuniversal Jones subfactorでprincipal graph A4m-3の場合や,その一般化であるRadulescuやBocaのsubfactorなど,多くの例に適用することができる.また,この結果の応用例として,principal graph A5のindex=3のsubfactorに対してGoldman’s type theoremを示す. 第3章では,Evans-KawahigashiやXuによって得られた,ある種のpartition functionの値を用いることによって,non-AFDのSU(n)ksubfactorに対しても,Evans-KawahigashiやXuによるAFD II1の場合と同様に,orbifold constructonが行えることを示す. このpartition functionの値がwell-definedになるために,まずsubfactorのconnectonを対称に取る必要がある.そこで,より一般的な状況のもとで,symmetric connectionがとれるための十分条件を与えた.次に問題となるのが,non-strongly outer alltomorphismのLoi invariantのtrivialityである.A型からD型へのorbifold construction(SU(2)k subfactorにあたる)の場合にはA型のsubfactorがJones projectionだけで生成されていたため,Loi invariantのtrivialityは明らかであったが,一般のSU(n)k subfactorの場合には,これは明らかではない.そこで,subfactorがsymmetric connectonを持つ場合に,ある種のpartition functionの値と関連づけることにより,non-strongly outer automrphismのLoi invariantがtrivialになるための必要十分条件を与えた.この結果は,またSU(n)k subfactorのrelative.Connes invariant X(M,N)の決定に対する,解答を与えるものでもある. これらの結果を,適用することにより,SU(n)k subfactorの場合に,orbifold con-structionがAFDでない場合に一般化できることが示される. 第4章では,subfactor N ⊂ Mに,新たな代数的不変量を導入した.これは,non-strongly outerかつLoi invarinatがtrivialなautomorphismの集合を,normalizerからくるinner automorphismで割ったもので,勝手なsubfactorに対して,群を対応させるものである.この不変量はsubfactorがAFD II1でstrongly amenableの時には,河東によって定義されたrelative Connes invariant X(M,N)に一致することがわかる. ここでは,この代数的relative Connes invariant 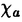 (M,N)が,つねに可換群をなすことを,勝手なsubfactorのnon-strongly outer automorphismがLoi invarinatのtrivialなautomorphismとinner automorphismを除いて可換であるという,より強い形で証明を与える.また,数人の人々によって,subfactorのrelative Connes invariant X(M,N)とtype III factorのmodular automorphismとの類似が指摘されている.これに関して,modular automorphismの場合,Connesの非可換Radon-Nikodym cocycle定理によって,外部自己同型群の中心に含まれるが, (M,N)が,つねに可換群をなすことを,勝手なsubfactorのnon-strongly outer automorphismがLoi invarinatのtrivialなautomorphismとinner automorphismを除いて可換であるという,より強い形で証明を与える.また,数人の人々によって,subfactorのrelative Connes invariant X(M,N)とtype III factorのmodular automorphismとの類似が指摘されている.これに関して,modular automorphismの場合,Connesの非可換Radon-Nikodym cocycle定理によって,外部自己同型群の中心に含まれるが,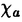 (M,N)に対しても,SU(n)k subfactor(level (M,N)に対しても,SU(n)k subfactor(level 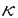 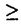 n+1)など多くのおもしろい例において,この類似が成り立つ(すなわち, n+1)など多くのおもしろい例において,この類似が成り立つ(すなわち,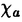 (M,N)がsubfactor N ⊂ M の外部自己同型群の中心に含まれる)ことがわかる. (M,N)がsubfactor N ⊂ M の外部自己同型群の中心に含まれる)ことがわかる. 最後に,orbifold constructionの最も一般的な定義を与えた.この定義と,ここで示した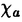 (M,N)がAbel群になるという結果から,orbifold actionはつねに可換なものから生じることがわかる. (M,N)がAbel群になるという結果から,orbifold actionはつねに可換なものから生じることがわかる. |
| 審査要旨 | | 論文提出者,後藤聡史は,V.F.R.Jonesによって創始された,作用素環論におけるsub-factor理論の,代数的,組合せ論的側面を主に研究している.その中心テーマは,subfactorに対して現れる,量子化されたGalois群ともいうべき,paragroupである.特にこの論文においては,subfactor/paragroupに対するorbifold constructionといわれる構成が非常に一般的な枠組みで研究されている. Orbifold constructionは,もともと共形場理論で考えだされたものであるが,subfactor理論においては,これまで河東,Evans,Xuらによって応用されて来た.Orbifold constructionというのは,おおざっぱに言えば,paragroupが通常の有限群をその「一部」として含むときに,その有限群の部分を使ってsubfactorやparagroupを作りかえるからくりであるが,これまでの応用では常に,AFD(approximately finite dimensional)という解析的条件が仮定されて来た.しかし,これはparagroup自体の構造を扱う構成法なので,関数解析的な分類理論は必要なく,その種の分類理論の前提であるAFDという仮定も不要であるはずだと何人もの人が予想していた.後藤聡史は,本論文でこの予想の証明をはばんでいた困難を新しい手法で乗り越え,orbifold constructionを一般的な方法で完成させた.この結果はPopaやRadulescuらによって構成されているnon-AFD SU(n)k subfactorなど,多くの例に適用することができることがわかっている. 本論文ではまず,subfactorのtypeによらずに,principal graphと呼ばれる不変量がDynkin図形A4m-3である場合に,Popa,長田-幸崎の意味でのnon-strongly outer automorphismによる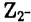 同時接合積をとることによって,principal graph D2mを持つsubfactorに作り替えられることが示された.この結果は,orbifold constructionのもっとも基本的な場合をカバーするもので,これまでAFDという仮定付きでしかできていなかったものである.本論文では,AFDの場合に計算されていたあるpartition functionの計算式が,まったく別の式に現れる係数と同一視できることを示すことによって,テクニカルな困難を乗り越えている.この応用として,泉によるindex 3の場合のGoldman type theoremの簡単な別証も得られる. 同時接合積をとることによって,principal graph D2mを持つsubfactorに作り替えられることが示された.この結果は,orbifold constructionのもっとも基本的な場合をカバーするもので,これまでAFDという仮定付きでしかできていなかったものである.本論文では,AFDの場合に計算されていたあるpartition functionの計算式が,まったく別の式に現れる係数と同一視できることを示すことによって,テクニカルな困難を乗り越えている.この応用として,泉によるindex 3の場合のGoldman type theoremの簡単な別証も得られる. この例は,Wess-Zumino-Witten modelの立場からは,SU(2)kに対して,orbifold constructionを行ったと思える.そこで,これをSU(n)kに対して一般化しようというのが,次の話題である.これは,AFDという仮定付きでは,Evans-KawahigashiやXuによって行われており,特にXuはflatnessに対するobstructionがconformal dimensionによって定まることを証明した.本論文では,AFDという仮定なしに,あるpartition functionの値に別の意味付けを与えるが,そのためにはまずsubfactorのconnectonを対称に取る必要がある.そこで,より一般的な状況のもとで,symmetric connectionがとれるための十分条件を最初に与えている.次に問題となるのが,non-strongly outer automorphismのLoi invariantのtrivialityである.SU(2)の場合にはこの事実はまったく明らかであったが,一般のSU(n)kの場合には,これは少しも明らかではない.そこで本論文では,subfactorがsymmetric connectonを持つ場合に,ある種のpartition functionの値を用いて,non-strongly outer automrphismのLoi invariantがtrivialになるための必要十分条件を与えた.この結果は,またSU(n)k subfactorのrelative Connes invariant X(M,N)の決定に対する,解答を与えるものでもある.さらに,この方法は,Xuによるflat partの計算についても,より強い結果をはるかに短い計算で出すことができる. また本論文の最後では,orbifold constructionに現れるautomorphismが河東によって導入されたrelative Connes invariant X(M,N)と深く関わっていることから,AFDでない場合に,より代数的な不変量algebraic relative Connes invariant 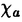 (M,N)を導入し,これがつねに可換群になることを示した.この (M,N)を導入し,これがつねに可換群になることを示した.この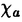 (M,N)を用いて最も一般的な状況におけるorbifold constructionについても議論がなされている.特に,orbifold actionはつねに可換なものから生じることがわかる. (M,N)を用いて最も一般的な状況におけるorbifold constructionについても議論がなされている.特に,orbifold actionはつねに可換なものから生じることがわかる. よって論文提出者後藤聡史は,博士(数理科学)の学位を受けるに充分な資格があると認める. |