ウェーブレット解析は時間と周波数の情報を不確定性関係の範囲内で取り出せることから、地震記録などの非定常データの解析にとって欠くことのできない解析手法となりつつあり、主にデータ処理の分野で急速な発展を遂げている。これに対して、ウェーブレットによる微分方程式の数値解析への応用は、比較的緩やかな進捗となっている。現在まで提案されている数値解析手法の大部分はウェーブレットーガレルキン法に基づいており、一般にこの手法では作用素の表現行列に対する逆行列演算が必要とされ、計算時間の意味であまり実用的とはいえない。そのため近年、いくつかの提案がなされ始めている。Qianらは、解に周期境界条件を仮定することによりFFTを用いて、行列演算をベクトル演算に置き換えて計算することを提案している。またより基本的な対策として、方程式系に適合するウェーブレットを構成する方法が考えられる。この考え方としてDahlkeらは、偶数階線形微分作用素(d2n/dx2n)の表現行列をブロック対角とするような新しいウェーブレットの構成法を示した。一般に微分作用素の表現行列をブロック対角化するには、完全正規直交ウェーブレットではできないことから、彼らは直交条件をゆるめて双直交ウェーブレットによりブロック対角化を行った。さらにWilliamsらはその行列がほとんど対角行列となることを明らかにし、それによってオーダーnの高速の処理手続きで解が得られることを示した。 本論文では、彼らの手法を拡張し積分作用素への適用を行う。また、表現行列がブロック対角可能な積分作用素を用いることにより、奇数階微分方程式の解がオーダーnの処理手続きで得られることを示す。さらに本手法をデータの補正に関する実用的な問題に適用する。 方程式Au(t)=f(t)(A:線形作用素、u:未知関数、f:既知関数)を解くことを考える。一般に双直交ウェーブレットは、双直交性を考慮にいれた二つの多重解像度による、基本および共役シンボルm0(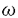 )、 )、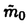 ( (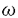 )を与えることにより構成可能である。そこでウェーブレットーガレルキン法による作用素Aの表現行列がブロック対角化されるための、m0( )を与えることにより構成可能である。そこでウェーブレットーガレルキン法による作用素Aの表現行列がブロック対角化されるための、m0(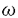 )と )と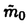 ( (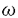 )に関する条件を求める。 )に関する条件を求める。 あるスケールjでのウェーブレットーガレルキン表現は、作用素Aの表現行列Kj(サイズ2j×2j)と、スケールjでの基本および共役スケール関数によるu(t)とf(t)の展開係数ベクトルcj、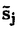 を用いて、 を用いて、 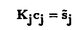 と表される。さらにスケールjからスケールj-1への分解を行うと、行列Kjは、次のようにそれぞれがサイズ2j-1×2j-1の4つの行列に分解できる。 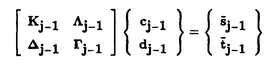 左辺の行列がブロック対角(i.e. j-1= j-1=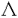 j-1=0 ∀j∈Z)となるためにはまず j-1=0 ∀j∈Z)となるためにはまず 0= 0=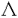 0=0が必要であり、このためには基本シンボルm0( 0=0が必要であり、このためには基本シンボルm0(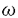 )と共役シンボル )と共役シンボル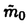 ( (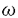 )の間に )の間に 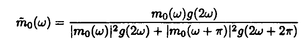 の関係が成り立てばよい。但し、g(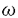 )は作用素Aに付随する関数 )は作用素Aに付随する関数 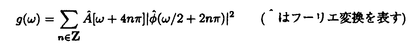 でありかつ、g(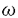 )= )=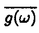 またはig( またはig(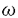 )が実関数であればよい。 )が実関数であればよい。 いま線形作用素Aとして 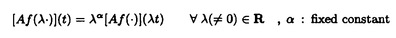 を満たす(スケール変換に不変)ものを考えると、 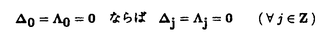 となる。これらのことより、以下の3つの条件を満たす場合は、作用素Aの表現行列がブロック対角化されることがわかる。 (i)作用素Aがスケール変換に不変であること。 (ii)共役シンボル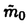 ( (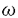 )が発散しないこと。 )が発散しないこと。 (iii)作用素Aに付随する関数g(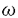 )が、g( )が、g(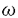 )= )=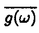 またはig( またはig(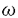 )が実関数であること。 )が実関数であること。 次に積分作用素に適合する双直交ウェーブレットの例を与える。 (a)Rieszポテンシャル 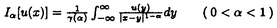 但し 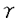 ( (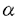 )= )=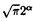 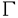 ( (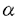 /2)/ /2)/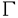 ((1- ((1-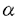 )/2)であり )/2)であり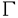 はGamma関数。作用素 はGamma関数。作用素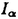 に付随する関数g( に付随する関数g(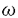 )は )は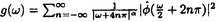 でありRieszポテンシャルは(i)から(iii)の条件を満たし、この積分作用素の表現行列は作用素に適合する双直交ウェーブレットによって、ブロック対角化される。 でありRieszポテンシャルは(i)から(iii)の条件を満たし、この積分作用素の表現行列は作用素に適合する双直交ウェーブレットによって、ブロック対角化される。 (b)Hilbert変換の1階微分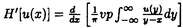 但し 但し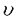 pは主値 pは主値 作用素H’に付随する関数g(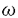 )は )は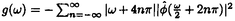 でありHilbert変換の1階微分は(i)から(iii)の条件を満たし、この積分作用素の表現行列も作用素に適合する双直交ウェーブレットによって、ブロック対角化される。 でありHilbert変換の1階微分は(i)から(iii)の条件を満たし、この積分作用素の表現行列も作用素に適合する双直交ウェーブレットによって、ブロック対角化される。 (c)Abel変換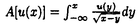 作用素Aに付随する関数g(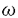 )は )は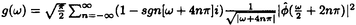 でありAbel変換は(i)と(ii)の条件は満たすものの(iii)の条件を満たさない。そのため、この積分作用素の表現行列は作用素に適合する双直交ウェーブレットによって、半ブロック対角( でありAbel変換は(i)と(ii)の条件は満たすものの(iii)の条件を満たさない。そのため、この積分作用素の表現行列は作用素に適合する双直交ウェーブレットによって、半ブロック対角( j-1=0 and j-1=0 and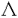 j-1≠0 for all j∈Z)となる。 j-1≠0 for all j∈Z)となる。 次に奇数階線形微分作用素に対して、その解を得る処理手続きがオーダーnとなるような手法を提案する。 Hilbert変換や奇数階微分作用素は、共役シンボル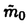 ( (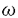 )が発散してしまうために、作用素に適合する双直交ウェーブレットを構成することができない。そこでまず、Hilbert変換の作用素(H)に対し、 )が発散してしまうために、作用素に適合する双直交ウェーブレットを構成することができない。そこでまず、Hilbert変換の作用素(H)に対し、 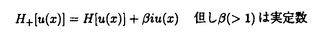 として得られる作用素(H+)を考えると、この作用素は条件(i)から(iii)を満たし、その表現行列は適合する双直交ウェーブレットによってブロック対角化できることがわかる。次に奇数階線形微分作用素(A=dl/dxl:l奇数)の逆作用素A-1が、作用素(H+)とRieszポテンシャルの作用素(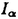 )によって、 )によって、 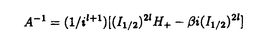 と表現されることに注意すると、作用素(I1/2)2lH+および(I1/2)2lの表現行列が、それらの作用素に適合する双直交ウェーブレットによりブロック対角化可能であることから、逆作用素A-1はブロック対角化可能な2つの作用素の線形結合として表現できることがわかる。これら2つの表現行列の行列要素の値は、その対角要素から離れるに従い指数的に減少するため、表現行列をバンド行列で近似することができる。従って、実用的な解を得る全体の処理手続きはオーダーnとなる。 最後に、実用的な問題への応用として上で得られた双直交ウェーブレットを用いて、データの補正を行いさらに積分処理を実行する一連の手法を提案する。 高層建物など固有周期の長い建築物に対して、地震観測などによって得られた加速度データに積分処理を実行して、速度データを求めることは重要な課題である。しかし実際に観測される加速度データには、種々の高周波あるいは低周波成分のノイズが混在したり、理論的にはあり得ないDC成分が生じる場合がある。そこで本手法のモデルデータ(継続時間は0から1秒)として、ある限られた範囲(データの中心0.5秒付近)に高周波成分のノイズが混在し、かつDC成分が生じているようなデータを考え、前章で得られた双直交ウェーブレットを用いて、時間一周波数領域でそれらの除去・補正を行い積分処理を実行する一連の処理を行う。初めに双直交ウェーブレットにより時間一周波数領域へのモデルデータの展開を行い、そこでのウェーブレット係数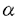 j,kでスケールjが最大でかつk/2j j,kでスケールjが最大でかつk/2j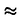 0.5のものを 0.5のものを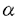 j,k=0として、ノイズの除去を実行する。次にDC成分の除去のため、線形作用素Fを双直交ウェーブレット j,k=0として、ノイズの除去を実行する。次にDC成分の除去のため、線形作用素Fを双直交ウェーブレット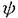 j,kに対し j,kに対し F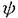 j,k=(1/Bj,k) j,k=(1/Bj,k)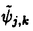 但しBj,kは(j,k)に依存した正の定数によって定義し、また新ノルム<・,・>Nとして 但しBj,kは(j,k)に依存した正の定数によって定義し、また新ノルム<・,・>Nとして 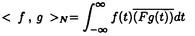 を導入して、除去前x(t)と除去後xap(t)のデータのノルム 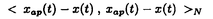 が、時刻t<0及びt>1でx(t)=0の条件のもとで、最小となるようにLagrangeの未定乗数法を用いて補正を実行する。このとき双直交ウェーブレットを用いることにより、時間一周波数に依存した重み係数Bj,kを導入することができ、より現実に即した補正が可能となっている。さらに補正後のデータの積分処理を行い、得られたデータを理論的に得られるデータと比較することにより、本手法の有効性を確認した。 以上本論文で得られた成果は、次のように要約することができる。 (1)ある特徴を有する積分作用素の表現行列は、その作用素に適合する双直交ウェーブレットによりブロック対角化できる。 (2)奇数階線形微分作用素の逆作用素を、ブロック対角化可能な積分作用素の線形結合で表現することにより、解を高速で得ることが可能である。 (3)積分処理を伴うデータ補正を双直交ウェーブレットを用いて行うことにより、従来困難であった時間一周波数領域でのデータ処理を可能にした。 |