一つのノルム空間E、あるいはその一部、から他のノルム空間Fへの等距離写像が必ずアフィンかどうかは古くからある重要な問題である。TがEからF上への写像である時この問題の答は肯定的である(S.MazurとS.Ulam[1])。TがEの凸体からFの凸体上への写像である時も答は肯定的である(P.Mankiewicz[2])。D.Tingley[3]は次の問題を提出した: Tingley問題:Tがノルム空間Eの単位球面SEからノルム空間Fの単位球面SF上への等距離写像である時、TはEへ延長されて線形またアファインな写像になるか? E、Fが有限次元ノルム空間の時、全射等距離写像T:SE→SFについてT(-x)=-Tx(∀x∈SE)が成り立つことはD.Tingley[3]により証明されたが、Tingley問題の完全な解決への見透しはたっていない。 この問題は非常に難しく、二次元空間でも一般にはわからないため、具体的なノルム空間ではどんな結論になるのかを考えてみた。著者は修士論文の中で:あるC0( ,E)型空間とこれら型の空間のl1-和に対してTingley問題を肯定的であることを示した。 ,E)型空間とこれら型の空間のl1-和に対してTingley問題を肯定的であることを示した。 本論文は修士論文の継続であるが、まず第一部でC0( ,E)型空間のlp-和(1<p<∞)においてTingley問題を肯定的に解決し同時にこの様な和の単位球面の等距離写像の形も具体的に見出した。そして、第二部でC0(n)(X)型(n ,E)型空間のlp-和(1<p<∞)においてTingley問題を肯定的に解決し同時にこの様な和の単位球面の等距離写像の形も具体的に見出した。そして、第二部でC0(n)(X)型(n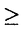 1,X⊆R局所コンパクトかつX⊆cl(int X))のノルム空間中の単位球面の間の等距離写像を詳細に研究し、これらの単位球面の等距離写像の形を具体的に与えた。これによってTingley問題の解決と(これまで特殊な場合にのみ知られていた)等距離作用素群の決定が可能になった。最後、第三部で一般m次元空間Rm中の開集合Xに対して新しいノルム空間(実際にはバナツハ代数)C0(n)(X)を導入し、今までm=1の場合しか知られない、C0(n)(X)中の等距離作用素と等距離作用素群の表現が得られた。 1,X⊆R局所コンパクトかつX⊆cl(int X))のノルム空間中の単位球面の間の等距離写像を詳細に研究し、これらの単位球面の等距離写像の形を具体的に与えた。これによってTingley問題の解決と(これまで特殊な場合にのみ知られていた)等距離作用素群の決定が可能になった。最後、第三部で一般m次元空間Rm中の開集合Xに対して新しいノルム空間(実際にはバナツハ代数)C0(n)(X)を導入し、今までm=1の場合しか知られない、C0(n)(X)中の等距離作用素と等距離作用素群の表現が得られた。 主要結果: 第一部で、C0( ,E)は局所コンパクトハウスドルフ空間 ,E)は局所コンパクトハウスドルフ空間 上のE-値連続な、∞で0となる、関数全体にノルム‖f‖=sup{‖f( 上のE-値連続な、∞で0となる、関数全体にノルム‖f‖=sup{‖f(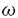 )‖: )‖: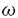 ∈ ∈ }を入れたノルム空間である。Xi,Yjは局所コンパクトハウスドルフ空間、Ci,Djはノルム空間(i∈ }を入れたノルム空間である。Xi,Yjは局所コンパクトハウスドルフ空間、Ci,Djはノルム空間(i∈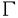 ,j∈ ,j∈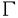 1)とし、Ei=C0(Xi,Ci),Fj=C0(Yj,Dj)のlp-和 1)とし、Ei=C0(Xi,Ci),Fj=C0(Yj,Dj)のlp-和 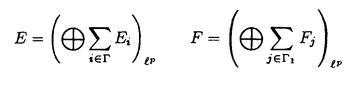 を考える、ただし1<p<∞。SEとSFはEとFの単位球面である。この時次の結論が成り立つ: 定理1. (1)A⊆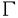 、A1⊆ 、A1⊆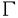 1かつ 1かつ 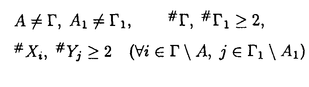 を満たし、Ei,Fjは狭義凸(i∈A,j∈A1)とする。このとき任意の全射等距離写像T:SE→SFに対して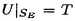 となる実線形な等距離作用素U:E→Fが存在する。 となる実線形な等距離作用素U:E→Fが存在する。 (2)もし#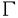 ,#Xi,#Yj ,#Xi,#Yj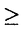 2かつCi,Djは狭義凸なノルム空間(i∈ 2かつCi,Djは狭義凸なノルム空間(i∈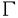 ,j∈ ,j∈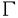 1)であれば、写像 1)であれば、写像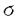 ,{ ,{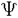 i:i∈ i:i∈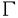 }と{ }と{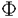 i:i∈ i:i∈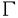 }が存在し: }が存在し: (a)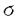 : :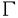 → →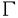 1は全単射であり, 1は全単射であり, (b)∀i∈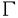 , ,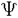 i:Xi→ i:Xi→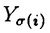 は同相写像であり, は同相写像であり, (c)∀i∈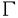 , ,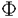 i:Xi×Ci→ i:Xi×Ci→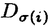 は連続、かつ は連続、かつ 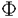 i(x,・):Ci→ i(x,・):Ci→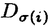 は全射実線形な等距離作用素(x∈Xiに対し)であり, は全射実線形な等距離作用素(x∈Xiに対し)であり, (d)任意のf∈SEに対し 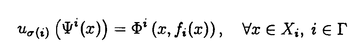 が成り立つ、ただしf=(fi),Tf=(uj)とする。 逆に、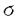 ,{ ,{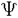 i:i∈ i:i∈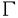 },{ },{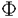 i:i∈ i:i∈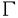 }が(a)〜(c)を満たせば、(d)で定義された写像TはSEからSFへの全射等距離写像である。 }が(a)〜(c)を満たせば、(d)で定義された写像TはSEからSFへの全射等距離写像である。 このほか、Lp( ,H)型空間(ここでHはHilbert空間)、抽象Lp-空間を含めて、のTingley問題も肯定的に解決された。 ,H)型空間(ここでHはHilbert空間)、抽象Lp-空間を含めて、のTingley問題も肯定的に解決された。 第二部で、n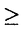 1は整数、XはR1の局所コンパクト部分集合(X⊆cl(int X))とする。C0(n)(X)はX上でn階までの連続導関数1を持ちかつ∞で0となる、すわなち、任意の 1は整数、XはR1の局所コンパクト部分集合(X⊆cl(int X))とする。C0(n)(X)はX上でn階までの連続導関数1を持ちかつ∞で0となる、すわなち、任意の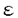 >0に対して >0に対して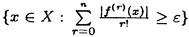 はXの中でコンパクトである、の関数全体にノルム はXの中でコンパクトである、の関数全体にノルム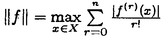 を入れたノルム空間である。Sn,xはC0(n)(X)の単位球面である。 を入れたノルム空間である。Sn,xはC0(n)(X)の単位球面である。 定理2.n,m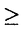 1は整数X,Y⊆R1はR1の局所コンパクト部分集合(X⊆cl(int X),Y⊆cl(int Y))とする。このとき次の結論が成り立つ: 1は整数X,Y⊆R1はR1の局所コンパクト部分集合(X⊆cl(int X),Y⊆cl(int Y))とする。このとき次の結論が成り立つ: (1)全射等距離写像T:Sn,X→Sm,Yがあればn=m; (2)もしT:Sn,X→Sn,Yが全射等距離写像であれば (h)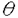 ’=0となる写像 ’=0となる写像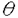 :Y→S1={ :Y→S1={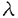 ∈K:| ∈K:|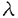 |=1}が存在し; |=1}が存在し; (i)|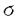 ’(y)|≡1(∀y∈Y)かつ ’(y)|≡1(∀y∈Y)かつ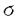 "=0となる同相写像 "=0となる同相写像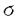 :Y→Xが存在し; :Y→Xが存在し; (j)A∪B=Y,A∩B=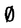 となるYの閉集合A,Bがあって; となるYの閉集合A,Bがあって; (k)任意のf∈Sn,Xに対し 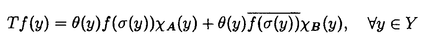 が成立する。ここでKは数係、XA,XBは定義関数である。 逆に、もし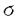 , ,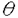 ,AとBが(h)〜(j)を満たせば(k)で定義した写像はSn,XからSn,Y上への等距離写像である。 ,AとBが(h)〜(j)を満たせば(k)で定義した写像はSn,XからSn,Y上への等距離写像である。 1x0∈Xでfの微係数は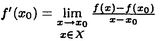 で定義する。 で定義する。 第三部で、Z+は非負整数の集合、XはRm(m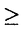 1)の部分開集合とする。m,n 1)の部分開集合とする。m,n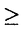 1に対し次の記号: 1に対し次の記号: 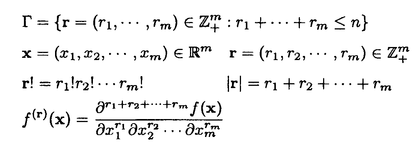 を採用し、C0(n)(X)はX上でf(r)∈C0(X)(r∈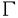 )を満たす関数fの全体にノルム )を満たす関数fの全体にノルム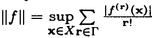 を入れたノルム空間(実際にはバナツハ代数)とする。前と同様Sn,XはC0(n)(X)の単位球面を示す。次の定理が成り立つ: を入れたノルム空間(実際にはバナツハ代数)とする。前と同様Sn,XはC0(n)(X)の単位球面を示す。次の定理が成り立つ: 定理3. (1)m1,m2,n1,n2 1を整数、X⊆Rm1,Y⊆Rm2を開集合とする。この時ノルム空間C0(n1)(X) 1を整数、X⊆Rm1,Y⊆Rm2を開集合とする。この時ノルム空間C0(n1)(X) C0(n2)(Y)の必要条件はm1=m2,n1=n2である。 C0(n2)(Y)の必要条件はm1=m2,n1=n2である。 (2)m,n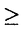 1を整数、X,Y⊆Rmを開集合とする。この時作用素T:C0(n1)(X)→C0(n2)(Y)が全射線形等距離写像になるの必要十分条件は次のものである: 1を整数、X,Y⊆Rmを開集合とする。この時作用素T:C0(n1)(X)→C0(n2)(Y)が全射線形等距離写像になるの必要十分条件は次のものである: (o)連続関数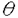 :Y→S1が存在して任意|r| :Y→S1が存在して任意|r|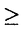 1に対し 1に対し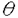 (r)=0; (r)=0; (p)同相写像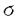 :Y→Xが存在してJ( :Y→Xが存在してJ(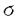 ):Y→IOR(m)は局所定数である; ):Y→IOR(m)は局所定数である; (q)任意のf∈C0(n)(X)に対し, 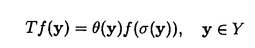 が成立する。ここでJ(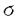 )は )は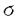 のJacobi行列、IOR(m)は(Rm,‖・ のJacobi行列、IOR(m)は(Rm,‖・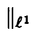 )上の(線形)等距離作用素の集合である。 )上の(線形)等距離作用素の集合である。 (3)m,n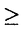 1を整数、X⊆Rmを開集合とする。この時C0(n)(X)の(線形)等距離作用素群は 1を整数、X⊆Rmを開集合とする。この時C0(n)(X)の(線形)等距離作用素群は × ×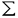 と同相である。ただし と同相である。ただし  で、 は一様位相(d( は一様位相(d(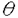 1, 1,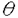 2)=sup{| 2)=sup{|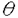 1(x)- 1(x)-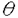 2(x)|:x∈X})、 2(x)|:x∈X})、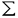 は離散位相である。また群演算は( は離散位相である。また群演算は(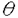 1, 1,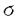 1)o( 1)o(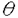 2, 2,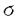 2)=( 2)=(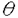 1・( 1・(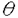 2o 2o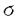 1), 1),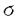 2o 2o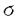 1)で定める。 1)で定める。 参考文献[1]S.Mazur and S.Ulam Sur les transformations isometriques d’espaces vectoriels normes,C.R.Acad.Paris 194(1932),946-948.[2]P.Mankiewicz On extention of isometries in normed linear spaces,Bull.Acad.Polon,Sci.Ser.Sci.Math.Astronomy,Phys.20(1972),367-371.[3]D.Tingley Isometries of the unit sphere,Geometriae Dedicata 22(1987),371-378. |