| 内容要旨 | | Rを離散付値環,KをRの商体,kをRの剰余体とする.この論文では,主に以下の問題を考える. 問題:XKをK上の非特異3次曲面とする.R上のgenericファイバーがXKと同型である"よい"整型スキームXがあるか? もちろん,この問題は,二部分に分かれる.まずは,"よい"というのは,なんでしょうか.そして,"よい"Xが存在するか. A.Corti[1]は以下の定義を提案した.非特異3次曲面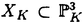 に対して,R上平坦な閉部分スキーム に対して,R上平坦な閉部分スキーム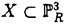 が,下の条件を満たせば,XKのstandard integral modelと呼ばれる. が,下の条件を満たせば,XKのstandard integral modelと呼ばれる. a).XのgenericファイバーがXKと同型で,specialファイバーが被約かつ既約である. b).Xが孤立cDV特異点しか持たない. Standard integral modelを作るために,Corti[1]は,具体的にプログラムを提案した.非特異3次曲面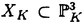 にCortiのプログラムを応用して,このプログラムが終止すれば,下のような整型閉部分スキーム にCortiのプログラムを応用して,このプログラムが終止すれば,下のような整型閉部分スキーム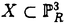 を得ることができる. を得ることができる. 1).XのgenericファイバーがXKと同型である; 2).XのspecialファイバーX0(XKの還元(reduction)ともいう)が被約かつ既約である; 3).X0上に,重複度2以上の直線がない; 4).X0上に,重複度3の点がない. Cortiは,Rが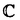 上の曲線上の局所環である場合(ここで幾何的な場合と呼ばれる)に,このようなXは,standard integral modelになることを証明した.Cortiは,彼の提案したプログラムが終止すると予想した.また幾何的な場合に,そのプログラムを終止させることができると証明した.したがって,幾何的な場合には,standard integral modelがある. 上の曲線上の局所環である場合(ここで幾何的な場合と呼ばれる)に,このようなXは,standard integral modelになることを証明した.Cortiは,彼の提案したプログラムが終止すると予想した.また幾何的な場合に,そのプログラムを終止させることができると証明した.したがって,幾何的な場合には,standard integral modelがある. 前述の問題は,整数論との繋がりを持つ.たとえば,H.P.F.Swinnerton-Dyer[4]は非特異3次曲面XKの還元X0上の有理点の研究によって,XK上の有理点のuniversal equivalence relationを研究した.(Yu.I.Manin and M.A.Tsfasman[3]参照). この論文では,まず,幾何的でない一般の場合には,前述の1),2),3),4)を同時に満たすXが存在しない例を挙げる. Theorem.R,K,kを前述と同様にして,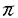 をRの極大イデアルの生成元とする.Kの標数が2,3でなく,また,任意のa∈k,a3≠2と仮定する.x1,x2,x3,x4を をRの極大イデアルの生成元とする.Kの標数が2,3でなく,また,任意のa∈k,a3≠2と仮定する.x1,x2,x3,x4を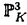 の斉次座標として,XKを以下の方程式で定義される非特異3次曲面とする. の斉次座標として,XKを以下の方程式で定義される非特異3次曲面とする. 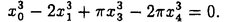 このXKに対して,任意の前述の1)を満たす整型閉部分スキーム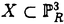 のspecialファイバーX0の上に,重複度は3の直線がある. のspecialファイバーX0の上に,重複度は3の直線がある. 次に,K上の非特異3次曲面XK上の27本の直線がK上に定義される場合に,前述の問題を考える. Theorem.R,K,kを前述と同様にして,K上の非特異3次曲面XK上の27本の直線がK上に定義されると仮定する.u,v,w,tを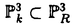 の斉次座標とする.このXKに対して,以下の条件のうちの一つと前述の1)を満たす整型閉部分スキーム の斉次座標とする.このXKに対して,以下の条件のうちの一つと前述の1)を満たす整型閉部分スキーム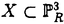 存在する. 存在する. 1°.XのspecialファイバーX0が以下のような方程式で定義される. 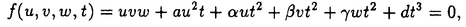 a,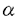 , ,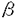 , ,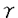 ,d∈k,fは既約.この場合は,X0が被約かつ既約で,たかだか重複度2の孤立特異点しか持たない. ,d∈k,fは既約.この場合は,X0が被約かつ既約で,たかだか重複度2の孤立特異点しか持たない. 2°.XのspecialファイバーX0が以下のような方程式で定義される. 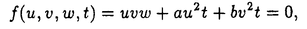 a,b∈k,a≠0,b≠0.この場合は,X0が被約かつ既約で,重複度2の直線u=v=0を持つ.X0のすべての特異点が,直線u=v=0の上にあり,その重複度は2. 最後に,二つの直線を持つ非特異3次曲面上の有理点のuniversal equivalence relation(Manin[2])を考える. Theorem.Kを無限体として,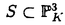 を二つの直線l1,l2を持つ非特異3次曲面とする. を二つの直線l1,l2を持つ非特異3次曲面とする. (1).l1∩l2=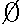 だったら,S上のすべてのK-有理点が一つのuniverssl equivalence classに属する. だったら,S上のすべてのK-有理点が一つのuniverssl equivalence classに属する. (2).l1∩l2≠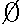 だったら,S上のK-有理点のuniversal equivalence clssが多くとも二つある.この場合に,universal equivalence classが一つしかないのと,下の条件とは同値. だったら,S上のK-有理点のuniversal equivalence clssが多くとも二つある.この場合に,universal equivalence classが一つしかないのと,下の条件とは同値. Nをl1とl2で生成される平面とする.あるK-有理点x∈N,y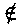 NとK上の直線 NとK上の直線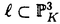 が存在して,lとSのintersection cycleがx+x+yであるか又は,x,y∈l⊂S. が存在して,lとSのintersection cycleがx+x+yであるか又は,x,y∈l⊂S. REFERENCES1.A.Corti,Del Pezzo surfaces over Dedekind schemes,Ann.of Math.?.2.Yu.I.Manin,Cubic Forms,2nd edition,North-Holland Publishing Company,1986.3.Yu.I.Manin and M.A.Tsfasman,Rational varieties,algebra,geometry and arithmetic,Russian Math.Surveys 41(1986),51-116.4.H.P.F.Swinnerton-Dyer,Universal equivalence for cubic surfaces over finite and local fields,Symposia Mathematica Bologna 24,Academic Press,1981,p.111-143. |